2º. Упрощение общего уравнения второй степени.
Общее уравнение кривой второго порядка относительно прямоугольных декартовых координат имеет вид
.
(2.8)
Применив преобразование поворота осей координат с использованием формул
(2.9)
освобождаясь в уравнении от члена с произведением координат, приходим к уравнению вида (2.7).
Примеры
Привести к каноническому виду уравнение
.
Решение. Преобразуем данное уравнение, воспользовавшись формулами (2.9) поворота осей координат:
,
или
.
Найдем
,
приравняв нулю коэффициент при
,
т. е.
,
или
.
Отсюда
,
;
примем
,
тогда
,
;
возьмем положительные значения
и
.
Тогда уравнение принимает вид
,
или
,
отсюда
.
Приняв за новое начало точку
,
применим формулы преобразования
координат
,
;
получим
,
или
.
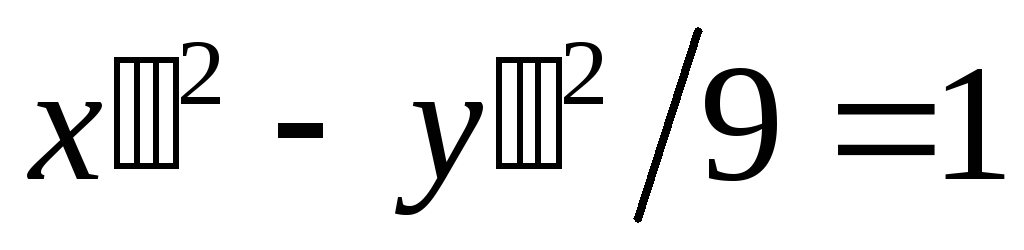Это уравнение гиперболы.
2.3. Поверхности второго порядка.
Поверхностью второго порядка называется
множество точек пространства, декартовы
координаты
которых удовлетворяют алгебраическому
уравнению второй степени
.
(2.10)
Это уравнение называется общим уравнением поверхности второго порядка и может определять сферу, эллипсоид, однополостный или двуполостный гиперболоид, эллиптический или гиперболический параболоид, цилиндрическую или коническую поверхность второго порядка. Оно может также определять совокупность двух плоскостей, точку, прямую или не иметь геометрического смысла (определять мнимую поверхность).
При
,
,
общее уравнение принимает вид
и легко упрощается с помощью параллельного переноса осей координат, что позволяет сразу установить его геометрический смысл.
Канонические уравнения поверхностей второго порядка:
1. Эллипсоид:
.
2. Гиперболоид
а) однополостный:
;
б) двуполостный:
.
3. Конус второго порядка:
.
4. Параболоид
а) эллиптический:
;
б) гиперболический:
.
5. Цилиндр второго порядка
а) эллиптический:
;
б) гиперболический:
;
в) параболический:
.
Одним из основных методов исследования формы поверхности по ее уравнению является метод сечений.
Пример 1. Методом
сечений исследовать форму поверхности,
заданную уравнением
.
Решение. Будем пересекать
поверхность горизонтальными плоскостями
.
Из системы уравнений
или
видно, что при
уравнение не имеет решений относительно
,
т. е. рассматриваемая поверхность
целиком расположена ниже плоскости
.
При
в любом сечении получается эллипс с
полуосями
,
,
вырождающийся в точку
при
.
Дальнейшее уточнение формы поверхности
можно получить, если рассмотреть сечения
координатными плоскостями
и
.
Сечение плоскостью
дает кривую
,
т. е. параболу с параметром
,
вершиной в точке
,
и ветвями, направленными в сторону
убывания значений
.
Сечение плоскостью
дает параболу
с параметром
,
вершиной в точке
,
и аналогично направленными ветвями.
Заданная поверхность есть эллиптический
параболоид. Преобразование координат
,
,
(которое сводится к сдвигу начала в
точку
– вершину параболоида и обращению
направления оси
)
приводит его исходное уравнение к
каноническому виду:
.
2. Привести к каноническому виду
уравнение
.
Решение. Сгруппируем члены с
одинаковыми координатами:
.
Дополнив до полных квадратов выражения
в скобках, получим
,
или
.
Произведем параллельный перенос осей
координат, приняв за новое начало
координат точку
.
Формулы преобразования координат имеют
вид
,
,
.
Тогда уравнение поверхности запишется
так:
,
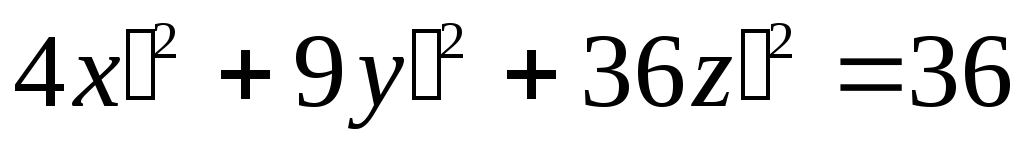или
.
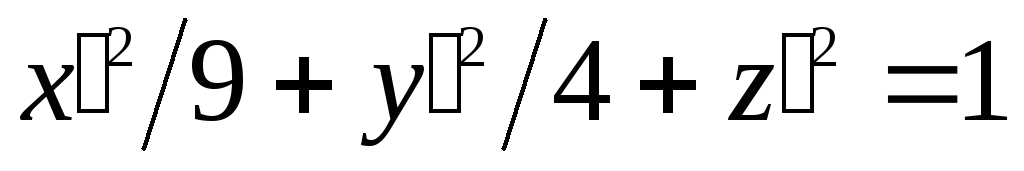Это уравнение определяет эллипсоид;
его центр находится в новом начале
координат, а полуоси соответственно
равны 3, 2 и 1.