5°. Уравнение плоскости, параллельной двум данным векторам.

Положение плоскости в пространстве также определено единственным образом, если известны два неколлинеарных вектора и , параллельных плоскости, и точка, через которую эта плоскость проходит. В качестве нормального вектора плоскости Р можно взять вектор векторного произведения , перпендикулярный к векторам и , а значит и к плоскости . Зная точку, через которую проходит плоскость Р, можно записать уравнение вида (1.18).

Также получить уравнение плоскости можно, выбрав произвольную точку плоскости Р и учитывая, что векторы и – компланарны. Значит, их смешанное произведение равно нулю, т. е. или в координатной форме получим равенство

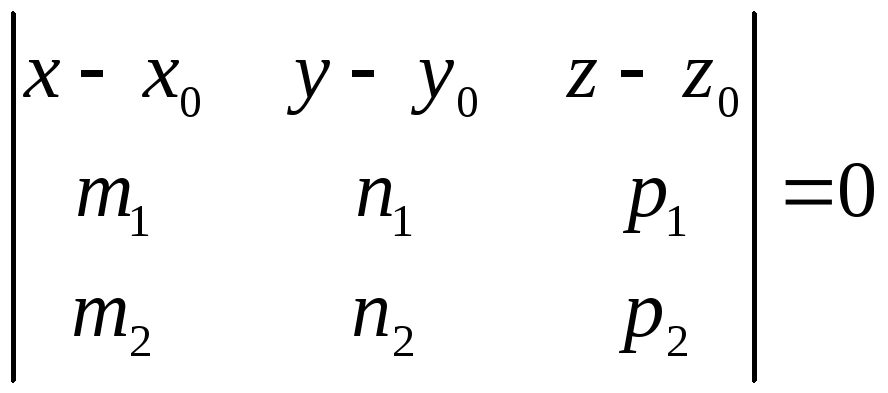, (1.23)

которое является уравнением плоскости, параллельной двум векторам и проходящей через точку .

6º. Уравнение пучка плоскостей.

Уравнение

(1.24)

при произвольном определяет некоторую плоскость, проходящую через прямую пересечения плоскостей и , т. е. некоторую плоскость, принадлежащую пучку плоскостей, проходящих через эту прямую. Такое уравнение называют уравнением пучка плоскостей.

7°. Угол между двумя плоскостями.

Величина угла между плоскостями и вычисляется на основании формулы

, (1.25)

где и – нормальные векторы данных плоскостей.

8^°. Условия параллельности и перпендикулярности двух плоскостей.

С помощью формулы (1.25) можно получить условие перпендикулярности двух плоскостей:

или . (1.26)

Если две плоскости параллельны, то параллельны и их нормальные векторы. Учитывая условие параллельности векторов, получаем условие параллельности двух плоскостей:

. (1.27)

9°. Расстояние от точки до плоскости.

Расстоянием от точки до плоскости Р: называется длина перпендикуляра, проведенного из этой точки на плоскость Р.

Искомое расстояние находится по формуле

. (1.28)

Оно равно взятому по абсолютной величине результату подстановки координат точки в нормальное уравнение плоскости. Знак результата этой подстановки характеризует взаимное расположение точки и начала координат относительно данной плоскости: “плюс”, если точка и начало координат расположены по разные стороны от плоскости, и “минус”, если они расположены по одну сторону от плоскости.

Примеры

1. Составить уравнение плоскости, проходящей через точку параллельно плоскости .

Решение. Т. к. искомая плоскость параллельна данной, то в качестве ее нормального вектора можно взять нормальный вектор данной плоскости. По формуле (1.18) получаем искомое уравнение:

или .

2. Уравнение плоскости привести к нормальному виду.

Решение. Находим нормирующий множитель (который берем со знаком “минус”, т. к.): . Итак, нормальное уравнение заданной плоскости имеет вид .

3. Из точки на координатные оси опущены перпендикуляры. Составить уравнение плоскости, проходящей через их основания.

Решение. Основаниями перпендикуляров, опущенных на координатные плоскости, служат следующие точки: , , . Используя соотношение (1.20), запишем уравнение плоскости, проходящей через три точки:

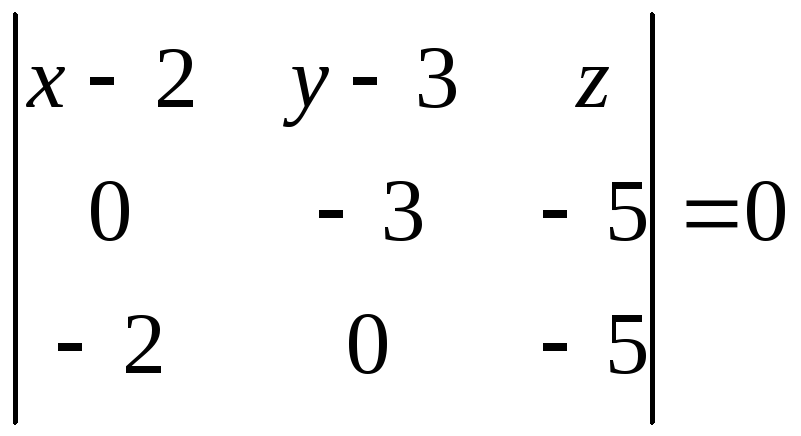или .

4. Составить уравнение плоскости, проходящей через точку и отсекающей равные отрезки на осях координат.

Решение. Используя уравнение (1.19) плоскости в отрезках, в котором имеем . Координаты точки А удовлетворяют уравнению искомой плоскости, поэтому выполняется равенство , откуда Итак, получаем уравнение .

5. Составить уравнение плоскости, проходящей через точки и перпендикулярной к плоскости

Решение. Уравнение плоскости, проходящей через точку можно записать в виде (1.18): .

Т. к. плоскость проходит и через точку то ее координаты удовлетворяют последнему уравнению, т. е. .

Искомая плоскость перпендикулярна к данной плоскости, поэтому на основании условия (1.26) Итак, для определения коэффициентов получена система уравнений

решение которой имеет вид

Подставляя его в уравнение, получим нужное уравнение плоскости

или

6. Составить уравнение плоскости, проходящей через точку и перпендикулярной к плоскостям и

Решение. В качестве нормального вектора искомой плоскости можно взять вектор, перпендикулярный нормальным векторам и данных плоскостей, т. е. векторное произведение векторов и :

Теперь, используя уравнение плоскости, проходящей через данную точку перпендикулярно вектору , получаем

или

7. Написать уравнение плоскости, проходящей через точки , параллельно вектору .

Решение. Задача имеет единственное решение, т. к. векторы и неколлинеарны. В качестве нормального вектора к плоскости может быть взят вектор

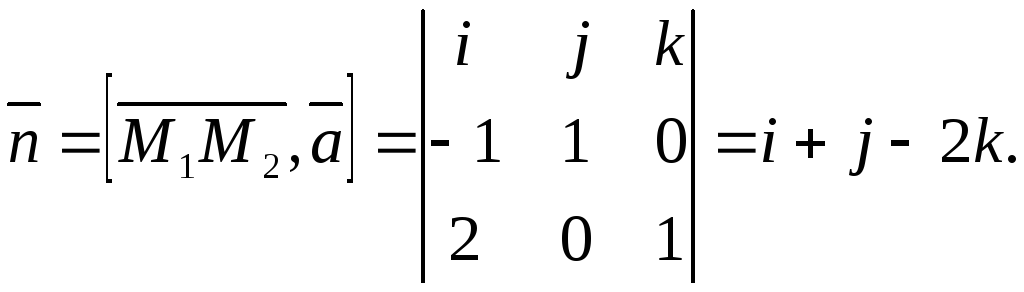
Уравнение плоскости имеет вид

или

Второй способ. Точка принадлежит искомой плоскости в том и только в том случае, когда векторы , и компланарны. Следовательно,

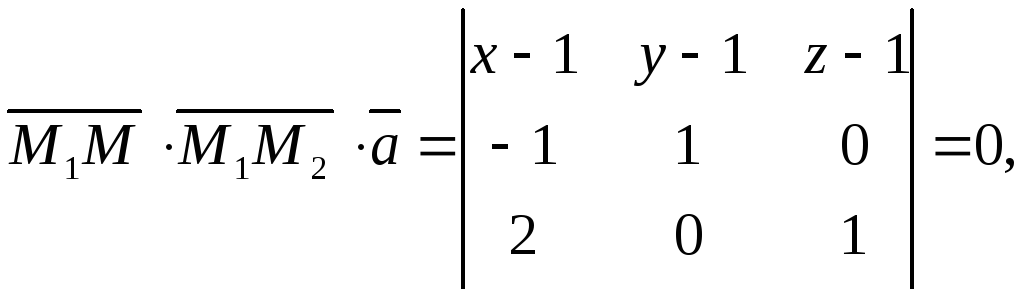
откуда

8. Две грани куба лежат соответственно на плоскостях Вычислить объем данного куба.

Решение. Достаточно найти длину ребра куба, равную расстоянию между данными параллельными плоскостями. Это расстояние равно расстоянию от любой точки одной плоскости до другой плоскости.

Выберем на первой плоскости произвольную точку. Приняв, например, что , , из уравнения найдем

По формуле (1.28) находим расстояние от точки до плоскости

.

Т. к. и то

9. Даны точки . Вычислить угол между координатной плоскостью и плоскостью

Решение. Используя формулу (1.20), составляем уравнение плоскости

откуда .

Нормальный вектор плоскости имеет координаты , нормальный вектор плоскости – . Тогда, в соответствии с формулой (1.25)

10. Составить уравнение плоскости, проходящей через линию пересечения плоскостей и и параллельной оси

Решение. Воспользуемся уравнением пучка плоскостей (1.24):

;

.

Так как искомая плоскость параллельна оси ординат, то коэффициент при должен быть равен нулю: , т. е. . Подставив найденное значение в уравнение пучка, получаем .