5°. Каноническое уравнение прямой

Если прямая проходит через точку параллельно вектору , называемому направляющим вектором прямой, то ее уравнение имеет вид:

. (1.7)

Равенство (1.7) называется каноническим уравнением прямой на плоскости.

6°. Параметрические уравнения прямой

В силу коллинеарности векторов и существует число , такое что или . Отсюда , , т. е.

(1.8)

Уравнения (1.8) называются параметрическими уравнениями прямой на плоскости, проходящей через точку с направляющим вектором .

7°. Нормальное уравнение прямой

Если обе части общего уравнения прямой умножить на число (которое называется нормирующим множителем), причем знак перед радикалом выбрать так, чтобы выполнялось условие , то получается уравнение

. (1.9)

Это уравнение называется нормальным уравнением прямой. Здесь р – длина перпендикуляра, опущенного из начала координат на прямую, – угол, образованный этим перпендикуляром с положительным направлением оси .

8°. Угол между двумя прямыми

Под углом между двумя прямыми будем понимать наименьший угол, на который надо повернуть одну прямую, чтобы она стала параллельна или совпала с другой прямой .

1. Если прямые заданы общими уравнениями и , то косинус угла между ними находится как косинус угла между их нормальными векторами и по формуле

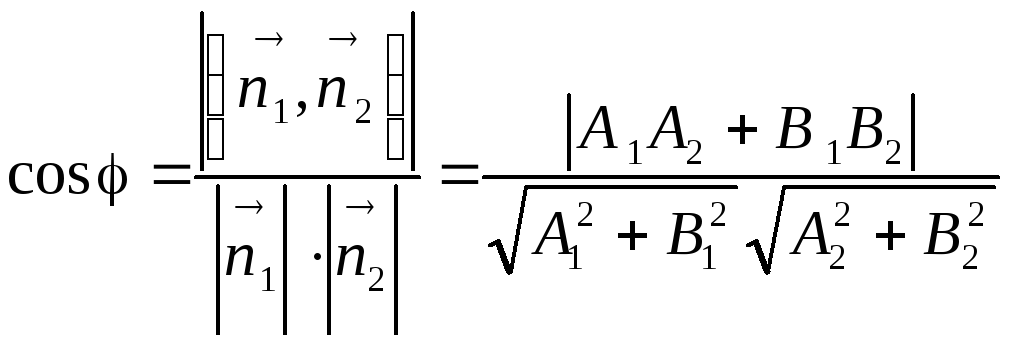. (1.10)

Условие перпендикулярности этих прямых имеет вид

, (1.11)

а условие их параллельности

. (1.12)

2. Если прямые заданы уравнениями вида (1.3) и , то угол между ними находится по формуле

. (1.13)

Для того чтобы прямые были параллельны, необходимо, чтобы выполнялось равенство , а для их перпендикулярности необходимо и достаточно, чтобы .

3. Если прямые заданы каноническим уравнением (1.7), то в этом случае , т. е.

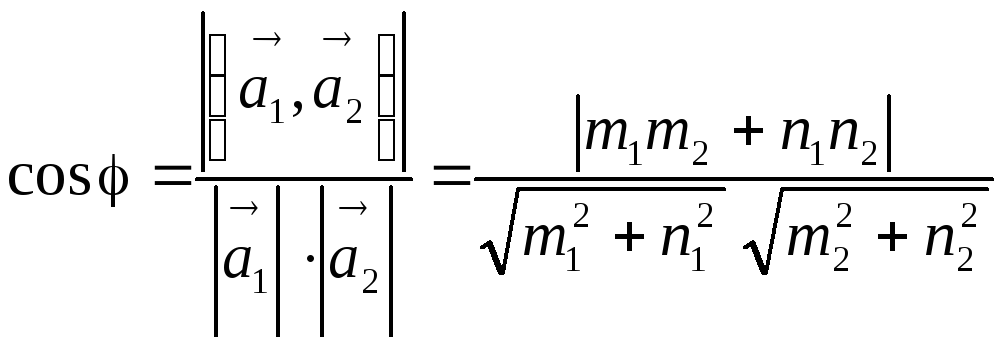. (1.14)

9°. Пересечение прямых. Расстояние от точки до прямой. Пучок прямых

Если , то координаты точки пересечения прямых и находятся путем совместного решения уравнений этих прямых.

Расстояние от точки до прямой находится по формуле

. (1.15)

Если пересекающиеся прямые заданы уравнениями и , то уравнение

, (1.16)

где – числовой множитель, определяет прямую, проходящую через точку пересечения заданных прямых. Давая в уравнении (1.16) различные значения, будем получать различные прямые, принадлежащие пучку прямых, центр которого есть точка пересечения заданных прямых.

Примеры

1. Материальная точка, выйдя из начала координат, движется прямолинейно и перпендикулярно вектору . Найти уравнение траектории и построить ее.

Решение. Так как траектория прямолинейна и выходит из начала координат, то уравнение траектории должно иметь вид . А т. к. коэффициенты А и В есть координаты нормального вектора, то, подставляя вместо А число 2 и вместо В число – 3, получим уравнение траектории .

Для построения траектории кроме точки достаточно построить еще одну какую-нибудь точку, например, .

2. Дано общее уравнение прямой . Написать:

а) уравнение с угловым коэффициентом;

б) уравнение в отрезках;

в) нормальное уравнение.

Решение. а) Разрешив уравнение относительно , получаем уравнение прямой с угловым коэффициентом:

.

Здесь , .

б) Перенесем свободный член общего уравнения в правую часть и разделим обе части на 65; имеем . Переписав последнее уравнение в виде

,

получим уравнение данной прямой в отрезках. Здесь , .

в) Находим нормирующий множитель (знак противоположен знаку свободного члена общего уравнения). Умножив обе части общего уравнения на этот множитель, получаем нормальное уравнение прямой

.

Здесь , , .

3. Написать уравнение прямой, проходящей через точку пересечения двух прямых и параллельно вектору .

Решение. Найдем точку пересечения двух данных прямых. Для этого решим систему уравнений:

Решением системы является , , т. е. точка пересечения двух прямых имеет координаты .

Для составления уравнения прямой воспользуемся формулой (1.7), взяв в качестве координат направляющего вектора координаты вектора, и в качестве точки, через которую проходит прямая – , имеем

.

Перепишем это уравнение в виде или .

4. Составить параметрическое уравнение прямой, проходящей через точку перпендикулярно к прямой .

Решение. Прямая или имеет нормальный вектор . Этот же вектор является направляющим вектором для искомой прямой. Воспользовавшись формулой (1.8), получим параметрические уравнения прямой, проходящей через точку с направляющим вектором :

5. Составить уравнение прямой, проходящей через точки и .

Решение. Полагая , , , в уравнении (1.5), получаем или .

Итак, искомое уравнение имеет вид . Проверим, что уравнение составлено верно. Для этого достаточно показать, что координаты точек и удовлетворяют уравнению прямой. Действительно, равенства , выполняются тождественно.

6. Показать, что прямые и параллельны.

Решение. Приведя уравнение прямой к виду с угловым коэффициентом, получаем и . Угловые коэффициенты этих прямых равны: , т. е. прямые параллельны.

7. Показать, что прямые и перпендикулярны.

Решение. Координаты нормальных векторов к прямым и удовлетворяют условию перпендикулярности векторов (1.11): .

Следовательно, прямые перпендикулярны.

8. Составить уравнения прямых, проходящих через точку и образующих с прямой угол .

Решение. Угловой коэффициент заданной прямой равен . Пусть угловой коэффициент одной из искомых прямых равен . Так как угол между этими прямыми равен , то , т. е. , откуда и .

Решая каждое из полученных уравнений, находим и . Итак, уравнение одной из прямых запишется в виде (по формуле (1.4)) , т. е. , а уравнение другой прямой в виде , т. е. .

9. Вычислить высоту трапеции, основания которой лежат на прямых , .

Решение. Высота трапеции равна расстоянию между указанными прямыми, а это последнее – расстоянию от произвольной точки, одной из них до другой. Выберем какую-нибудь точку первой прямой. Положив, например, , из уравнения найдем ; получим точку . По формуле (1.15) вычисляем расстояние от точки до этой прямой:

.

Искомая длина высоты трапеции равна 2,5.

10. Даны уравнения высот треугольника : , и координаты вершины . Составить уравнения сторон треугольника.

Решение. Легко убедиться в том, что вершина не лежит ни на одной из заданных высот: ее координаты не удовлетворяют уравнениям этих высот.

Пусть – уравнение высоты и – уравнение высоты . Составим уравнение стороны , рассматривая ее как прямую, проходящую через точку перпендикулярно высоте . Так как угловой коэффициент высоты равен 3, то угловой коэффициент стороны равен , т. е. . Воспользовавшись формулой (1.4), получим уравнение стороны :

или .

Аналогично получаем , , и уравнение стороны имеет вид , т. е. .

Решив совместно уравнения прямых и , а также прямых и , найдем координаты вершин треугольника: и . Остается составить уравнение стороны (по ф. (1.5)):

, т. е. .

11. Даны координаты вершин треугольника : , , . Найти:

1. длину стороны ;

2. угол 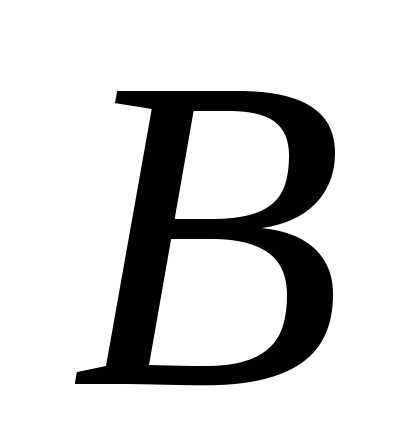в радианах;

3. уравнение сторон 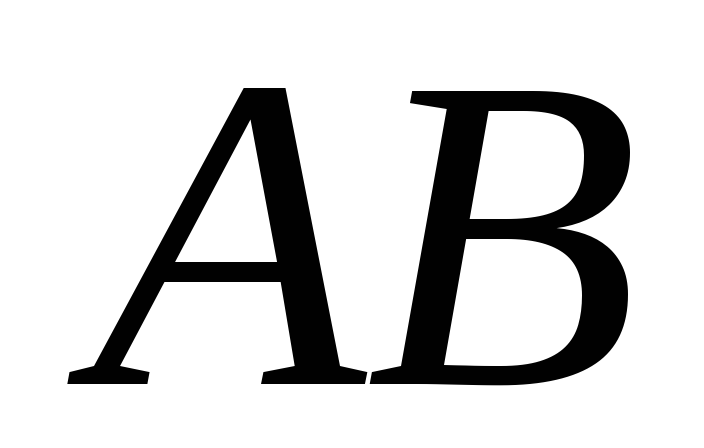и ;

4. уравнение высоты и ее длину;

5. уравнение медианы и координаты точки пересечения этой медианы с высотой ;

6. уравнение прямой, проходящей через точку , параллельно стороне ;

7. координаты точки , симметричной точке относительно прямой .

Решение. 1) Длину стороны найдем как расстояние между двумя точками: .

2) Угол найдем по формуле (1.13): , где и ; .

3) Уравнения сторон и найдем по формуле (1.5): , т. е. .

Аналогично для стороны : .

Чтобы найти угловые коэффициенты сторон и , запишем уравнения в виде прямых с угловыми коэффициентами:

и ,

отсюда , .

4) Уравнение высоты найдем как уравнение прямой, проходящей через данную точку по формуле (1.4): , где найдем из условия перпендикулярности прямых и : , т. е. .

Тогда уравнение высоты будет иметь вид: .

5) Уравнение медианы найдем, если найдем точку . Имеем

; , т. е. .

Тогда уравнение имеет вид .

Найдем координаты точки пересечения этой медианы с высотой , если решим систему уравнений высоты и медианы :

; .

6) Уравнение прямой, проходящей через точку , параллельно стороне , найдем по формуле (1.2), учитывая, что в качестве нормального вектора к искомой прямой может быть взят нормальный вектор прямой :

.

7) Найдем координаты точки , для чего решим совместно систему уравнений прямой и высоты :

; .

Чтобы найти координаты точки , расположенной симметрично точке относительно прямой , воспользуемся формулой деления отрезка пополам:

, , т. е.

, .

Откуда , .

12. Найти прямую, принадлежащую пучку и проходящую через точку .

Решение. Координаты точки М должны удовлетворять уравнению искомой прямой, поэтому для определения получаем уравнение или , то есть . Подставив значение в уравнение пучка, получим уравнение прямой , или .

13. Даны стороны треугольника: , и . Составить уравнение высоты треугольника, опущенной на сторону АС.

Решение. Высота принадлежит пучку , то есть .

Угловой коэффициент прямой пучка равен ; так как угловой коэффициент прямой АС равен , то угловой коэффициент искомой высоты равен 1 и для определения получаем уравнение . Отсюда , то есть . Подставив найденное значение в уравнение пучка, получим искомое уравнение высоты:

, то есть .