4. Эпюр №9

Тема. Определение коэффициентов искажения по аксонометрическим осям прямоугольной триметрии.

Содержание: В левой части листа выполнить прямоугольную триметрию детали, взяв индивидуальные задания в таблице 6. Оси симметрии определены на эпюре 8 и являются заданными к настоящей работе. Коэффициенты искажения по аксонометрическим осям определить, используя треугольник следов восьмого эпюра. В правой части листа выполнить стандартную прямоугольную диаметрическую аксонометрию той же детали. Образец выполнения задания на чертеже 9.

Пояснения

Реконструкция натурального координатного трехгранника по заданным аксонометрическим осям заключается в совмещении координатных плоскостей, образующих трехгранник, с плоскостью аксонометрических проекций путем вращения координатных плоскостей вокруг сторон треугольника следов (рис. 17). Из рисунка видно, что отношение длины отрезка АО₀ к длине отрез­ка АО или к длине отрезка АО₁ является коэффициентом искажения И по аксонометрической оси X₀, а отношение длины отрезка ВО₀ к длине отрезков ВО или ВО — показателем V по оси У₀.

Рассмотрим построение совмещенных координатных плоскостей на чертеже треугольника следов АВС, данного на рис. 18а. Совмещенная вершина трехгранника О₀ должна находиться на продолжении оси О₀ Z₀, так как точка О вращается в плоскости перпендикулярной оси вращения — прямой АВ. На стороне треугольника следов АВ, как на диаметре, строим полуокруж­ность (центр окружности лежит в точке, делящей отрезок АВ пополам). Точка пересечения оси О₀ Z₀ с полуокружностью является точкой О₁, т. е. совмещен­ным положением вершины координатного трехгранника О. Соединив точку O₁ с точками А и В, получим треугольник АO_│В, который является совмещен­ным положением натуральной координатной плоскости хоу. Аналогично про­изводится совмещение координатных плоскостей xoz, yoz.

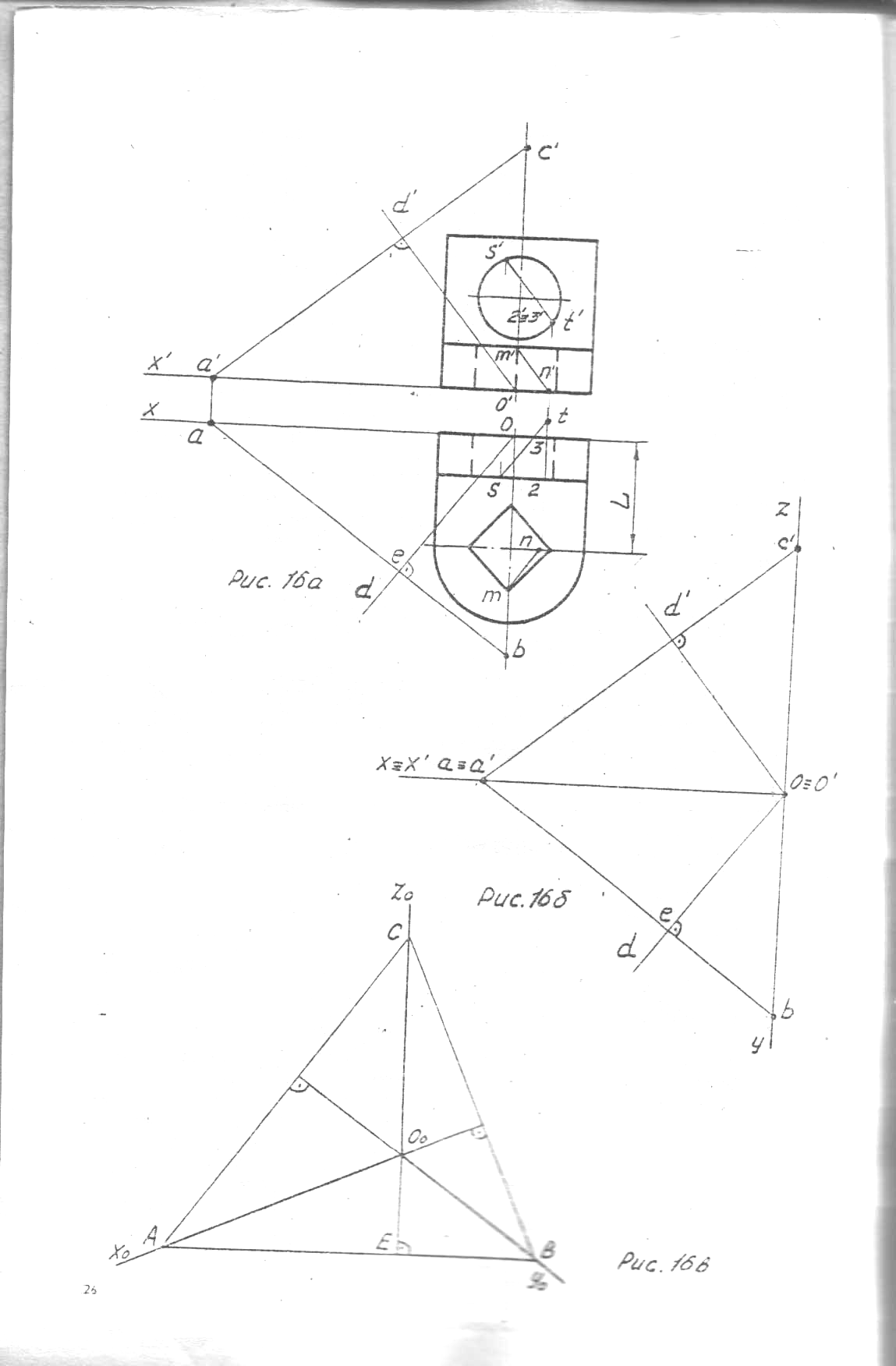
Реконструированный натуральный координатный трехгранник может быть использован для определения:

а) величин аксонометрических масштабов по известному натуральному масштабу, а, следовательно, и величин проекций отрезков, расположенных параллельно натуральным координатным осям;

б) показателей искажения;

в) величин малых осей эллипсов, изображающих окружности в аксоно­метрии.

На сторонах реконструированных координатных плоскостей откладываем отрезки, взятые на ортогональном чертеже предмета по соответствующим натуральным осям, например o₁v, o₂и, о₂w (рис. 18а). Затем возвращаем координатные плоскости обратным вращением в исходное положение. При этом построение на сторонах реконструированных плоскостей отрезки займут соответствующие положения на аксонометрических осях: o_│v₀, o₀и₀, о₀w₀. Эти отрезки являются аксонометрическими единицами измерения всех парамет­ров заданной детали, параллельных натуральным координатным осям х, у, z.

Отношения полученных аксонометрических единиц к истинной величине длины являются показателями искажения по аксонометрическим осям.

Чтобы упростить определение аксонометрических единиц измерения, можно пользоваться угловым графическим масштабом (рис. 186). Для постро­ения масштаба необходимо на его горизонтальной шкале отложить натураль­ные единицы измерения, а на вертикальной прямой — аксонометри­ческие единицы измерения u₀, v₀, w₀. Через полученные точки проводим наклонные линии ou₀, ov₀, оw₀. Определение аксонометрических единиц изме­рения проходит аналогично построению самого масштаба: например, длину детали L откладываем сначала на горизонтальной шкале масштаба, из получен­ном точки по вертикали берется отрезок L₀ до соответствующей линии У₀. Ана­логично определяются аксонометрические единицы измерения всех парамет­ров детали по осям x₀, y₀, z₀ .

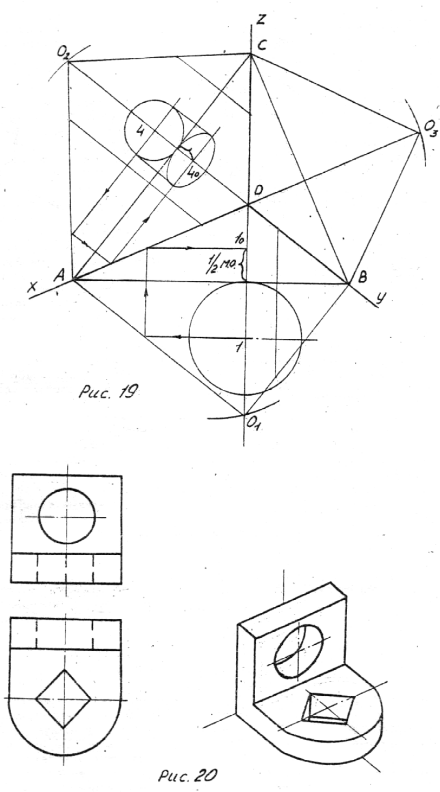
Рассмотрим определение величин большой и малой осей эллипса, кото­рой является аксонометрической проекцией окружности. Так как плоскости окружности в наиболее распространенных примерах расположены параллель­но одной из координатных плоскостей, то большая ось эллипса параллельна соответствующей стороне треугольника следов и равна по величине диаметру изображаемой окружности. Малая ось перпендикулярна к большой, ее вели­чина может быть определена на реконструированном натуральном трехгран­нике так, как показано стрелками на рис. 19.

Порядок выполнения эпюра

1. На треугольнике следов АВС листа 8 произвести его реконструкцию, по­строив натуральные плоскости AO₁B, АО₂С.

2. На сторонах натуральных плоскостей AO₁, AO₂ откладываем размеры детали, параллельные оси ОХ на ортогональном чертеже и проецируем их на аксонометрическую ось ОХ.

3. На стороне натуральной плоскости О₂С откладываем размеры детали по высоте и проецируем их на аксонометрическую ось OZ.

4. На стороне натуральной плоскости O_│B откладываем размеры детали, параллельные оси ОУ на ортогональном чертеже и проецируем их на аксоно­метрическую ось ОУ.

5. Используя аксонометрические единицы измерения, полученные на осях ОХ, ОУ, ОГ на листе 9 строим прямоугольную триметрию по осям, построен­ным на восьмом листе при выбранном направлении проецирования OD (od, o’d’).

6. На правой половине листа 9 строим прямоугольную диметрическую проекцию той же. детали, сравнивая наглядность обоих изображений.

7. Выполнив чертеж карандашом тонкими линиями, обводим его тушью основными сплошными линиями, за исключением осей вращения отверстий и аксонометрических осей.

В аксонометрии тень любой прямой на плоскость, перпендикулярную прямой, направлена параллельно вторичной проекции луча на ту же плоскость.

В аксонометрии тень любой прямой на плоскость, параллельную к ней, параллельна самой прямой.

Рассмотрим пример построения теней детали на образце выполнения за­дания (чертеж 10). Вначале определяем теневую образующую МN на поверх­ности цилиндрической стенки, отделяющую ее освещенную часть от части, находящейся в собственной тени. Для определения положения этой образую­щей проводим прямую, параллельную к вторичной проекции светового луча на плоскость XOZ (на плоскость, параллельную основанию цилиндрического свода) и касательную к цилиндрической кривой СДN. Точка касания N проек­ции луча и кривой определяет теневую образующую МN; а контур собственной тени вертикально-стоящей стенки детали определяется точками еЕМNDС с кри­вой, ограничивающей поверхность, противоположную направлению света.

Падающую тень этой части предмета строим на основе первого правила темы; строя тень каждой точки, например, тень Е. точки Е определяется пересечением вторичной проекции светового луча еЕ. и луча ЕЕ.. Тени от вертикальных углов стенки Ее, Сс направлены параллельно вторичной про­екции луча света на плоскости ХОY, и частично на поверхности горизонталь­ной плиты основания.

Как и выше определяем теневую образующую Аа на поверхности цилин­дрического скругления плиты основания, проведя прямую АА_1, параллельную вторичной проекции светового луча на плоскость ХОУ и касательно к цилинд­рической кривой. Падающая тень от плиты основания строится аналогично предыдущим построениям.

Для построения тени на внутренней стенке цилиндрического отверстия плиты вначале определяем вертикальную теневую образующую, отделяющую освещенную часть стенки от находящейся в собственной тени; для чего про­водим вторичную проекцию луча на плоскость верхнего основания отверстия плиты так, чтобы она касалась очертания отверстия в точке Q. Затем строим тень, падающую от верхнего криволинейного контура отверстия. Через про­извольно выбранную точку Т проводим вторичную проекцию луча света ТИ сначала горизонтально по плоскости верхнего основания отверстия, затем па­раллельно образующим цилиндрического отверстия, т. е. вертикально; также через точку Т проводим световой луч до пересечения с вторичной проекци­ей в точке Т.. Тень R. точки R определяется пересечением вторичной проекции светового луча rR. и луча RR..

Построив собственные и падающие тени детали, нужно закрасить их сла­бым раствором акварельной краски; собственные тени несколько светлее, падающие — темнее, одним и тем же цветом. После того, как акварель вы­сохнет, обвести чертеж тушью, выбирая толщину линий согласно ГОСТ 2.303-68.

Порядок выполнения эпюра

Выполняем прямоугольную изометрическую проекцию детали, учиты­вая в композиции листа и построение теней.

На аксонометрических осях строим горизонтальную и фронтальную проекции луча освещения s, s’, а также луч света S.

Строим собственные и падающие тени в отверстиях детали.

Определяем контур собственной тени детали.

Строим падающие тени заданной детали на поверхности самой детали и плоскости земли (стола).

Построив чертеж тонкими линиями карандашом, покрываем собствен­ные и падающие тени слабым раствором акварельной краски.

Когда акварель просохнет, чертеж обвести, контур детали — основной линией, контур теней и линии построения — тонкими сплошными линиями. Точки построения обозначить.