Свойства дисперсии

1. Дисперсия постоянной величины С равна нулю: Свойство становится ясным, если учесть, что постоянная величина сохраняет одно и то же значение и рассеяния, конечно, не имеет.

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

.

3. Дисперсия суммы или разности двух независимых случайных величин равна сумме дисперсий этих величин:

.

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии:

.

Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность совпадает с размерностью Х. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если Х выражается в линейных метрах, то будет выражаться также в линейных метрах, а – в квадратных метрах.

Случайная величина называется центрированной, если . Случайная величина называется нормированной (стандартной), если .

Вопросы для самопроверки

1. Что называют отклонением случайной величины от ее математического ожидания?

2. Чему равно математическое ожидание отклонения?

3. Как определяется дисперсия случайной величины?

4. Что характеризует дисперсия случайной величины?

5. По какой формуле можно вычислять дисперсию?

6. Каковы свойства дисперсии случайной величины?

7. Запишите формулу для дисперсии дискретной случайной величины, принимающей конечное множество значений.

8. Какой вид имеет формула для дисперсии дискретной случайной величины, принимающей счетное множество значений?

9. По каким формулам вычисляется дисперсия непрерывной случайной величины, все значения которой принадлежат отрезку ?

10. Как определяется дисперсия непрерывной случайной величины, все значения которой принадлежат бесконечному промежутку ?

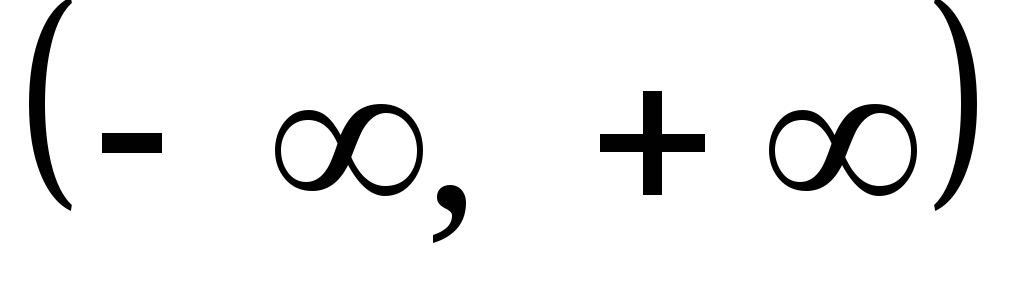11. Что такое среднее квадратическое отклонение?

Упражнения

1. Найти числовые характеристики случайной величины Х, заданной законом распределения:

а)	Х	0 1 2		б)	Х	– 0,1 0 0,1 0,4
	Р	0,3   0,2  0,5			Р	0,3   0,15  0,3 0,25

2. Найти числовые характеристики непрерывной случайной величины Х, заданной плотностью вероятностей:

а) б)

3. Случайная величина Х задана функцией распределения:

а) б)

Найти числовые характеристики .

4. Симметричная монета подбрасывается 4 раза. Случайная величина Х – число выпадений герба при этих подбрасываниях. Найти числовые характеристики случайной величины Х: .

5. Даны все возможные значения дискретной случайной величины Х: а также известны . Найти закон распределения случайной величины Х.

6. Дискретная случайная величина Х может принимать только два значения х₁ и х₂, причем . Известны вероятность и дисперсия . Найти закон распределения случайной величины Х.

7. Известны дисперсии двух независимых случайных величин . Найти дисперсию суммы этих величин.

8. Дисперсия случайной величины Х равна 5. Найти дисперсию следующих величин:

а) б) в) .

9. Случайная величина Х принимает только два значения: , каждое с вероятностью 0,5. Найти дисперсию этой величины.