5.4. Экономическая интерпретация множителей Лагранжа

Множители Лагранжа, вычисляемые при решении задачи оптимизации , показывают, как изменится величина функционала в окрестности точки экстремума при единичном изменении соответствующих ограничений, т. е.

.

В частности, если интерпретировать функционал как прибыль, а –как объемы располагаемых ресурсов, то множители Лагранжа будут численно равны изменению прибыли при единичном изменении этих ресурсов, т. е. это теневые цены ресурсов.

Приведем вывод для случая двух переменных и одного ограничения

.

Обозначим точку экстремума как . При изменении величины ограничения b ее координаты будут соответственно изменяться, следовательно, их можно рассматривать как некоторые функции от b. Тогда имеем:

и дифференцируя, получим:

.

Функция Лагранжа рассматриваемой задачи имеет вид

,

следовательно, в точке экстремума выполняются условия:

.

Таким образом,

.

После подстановки в производную от величины функционала получим

.

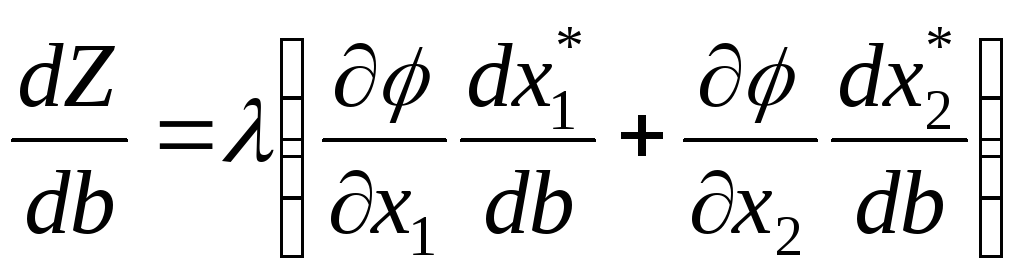Заключенное в скобки выражение равно единице, поэтому , что и требовалось доказать.

5.5. Градиентные методы

Градиентные методы универсальны и применяются для решения всех нелинейных задач, но любая их конкретная реализация (в том или ином пакете прикладных программ) имеет определенные функциональные ограничения. Эти методы требуют значительного числа итераций, чтобы с достаточной точностью найти экстремум. Поэтому их применение предполагает использование вычислительной техники. Рассмотрим возникающие проблемы, используя для этого графические примеры и не вдаваясь в детали реализации используемых алгоритмов.

Простейший пример может быть таким: предположим, что в условиях густого тумана нужно подняться на самую высокую точку незнакомой холмистой местности. Очевидно, что начинать движение надо в направлении самого крутого подъема, а если использовать более строгую терминологию, то надо перемещаться в направлении , где функция есть высота в точке с координатами . Заметим, что можно использовать не только информацию о направлении вектора градиента, но и о его величине. Действительно, чем больше модуль этого вектора, тем увереннее (с большим шагом) следует перемещаться. Если вычислить вторые частные производные, то можно учесть и скорость изменения вектора градиента. Однако увеличение эффективности таким путем требует дополнительных вычислений, поэтому для различных задач наиболее подходящими будут разные реализации градиентных методов.

Чтобы сократить число повторений расчетов производных часто используется метод наискорейшего подъема (спуска). Его суть в том, что после вычисления вектора градиента и выбора величины шага движение в выбранном направлении продолжается до тех пор, пока функция возрастает (для определенности считаем, что идет поиск максимума).

В достигнутой точке вычисляется новое значение вектора градиента и процесс повторяется. Если после вычисления градиента первый же шаг приводит к убыванию функции, то его надо уменьшить. Вычисления заканчиваются, когда шаг станет меньше заданной точности. На контурном рис. 5.7 (на него нанесены линии, соответствующие фиксированным значениям функции) показан возможный вариант движения от начальной точки к точке максимума .

x₂

0

x₁

Рис. 5.7

Однако если заданная функция имеет несколько максимумов, например, в точках , , а требуется найти глобальный максимум (на рис. 5.8 он в точке ), то нужно либо использовать дополнительную информацию о его местоположении и правильно выбрать начальную точку, либо искать все максимумы, чтобы потом выделить наибольший. Очевидно, что, выбирая в качестве начальной одну из точек , , , получим соответственно разные максимумы.

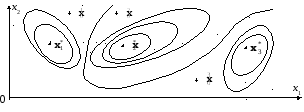
Рис. 5.8

Понимая экономическую сущность конкретной задачи, как правило, можно разумно выбрать начальную точку, а при наличии сомнений провести серию расчетов для некоторого набора начальных точек. Один из вариантов решения задачи в общем случае состоит в том, что последовательность начальных точек генерируется с использованием датчика случайных чисел, а достигнутые экстремумы запоминаются. Эти осложнения отсутствуют в задачах выпуклого программирования, для которых локальный и глобальный экстремумы совпадают.

Кроме оптимизации функционала, необходимо учитывать заданные ограничения. Если проверять их выполнение после каждого шага, и все они будут выполняться (оставаться неактивными), то они не будут влиять на процесс поиска оптимума, который будет найден во внутренней точке области допустимых решений. Когда очередной шаг приведет к нарушению хоть одного ограничения, алгоритм действий будет похож на действия водителя, оказавшегося на полосе встречного движения, пока не поздно надо вернуться на свою полосу. Определим, какое из ограничений нарушено в наибольшей степени, и в зависимости от знака отклонения будем двигаться по направлению градиента или антиградиента функции, определяющей это ограничение. Эта последовательность действий схематически показана на рис. 5.9.

Рис. 5.9

Чтобы сократить колебательные перемещения в окрестности границы области допустимых решений используются следующие подходы. Если нарушенное ограничение является линейным, то логично перемещаться, оставаясь на граничной гиперплоскости, соответствующей этому ограничению, в том направлении, которое образует с направлением градиента минимальный угол. Для нелинейных ограничений применяются методы штрафных и барьерных функций, суть которых в том, что целевая функция задачи заменяется некоторой обобщенной функцией (используются различные варианты), значения которой:

1.Совпадают со значениями исходного функционала внутри области допустимых решений.

2. Быстро возрастают при выходе за пределы этой области.

Таким образом, ценой усложнения функционала решение задачи на условный экстремум сводится к решению задачи на безусловный экстремум.