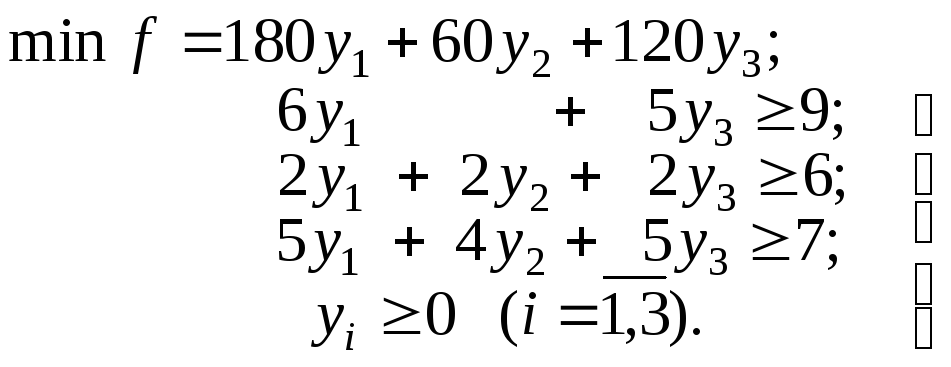3. Теория двойственности

3.1. Построение пары взаимно-двойственных задач

Будем называть исходную задачу линейного программирования прямой, а задачу, получаемую из нее по некоторым правилам, двойственной. Эти правила можно сформулировать в общем случае, но для простоты и наглядности изложения ограничимся симметричной формой задачи линейного программирования.

Рассмотрим в качестве прямой задачу оптимального использования ресурсов. Ее математическая модель имеет вид:

,

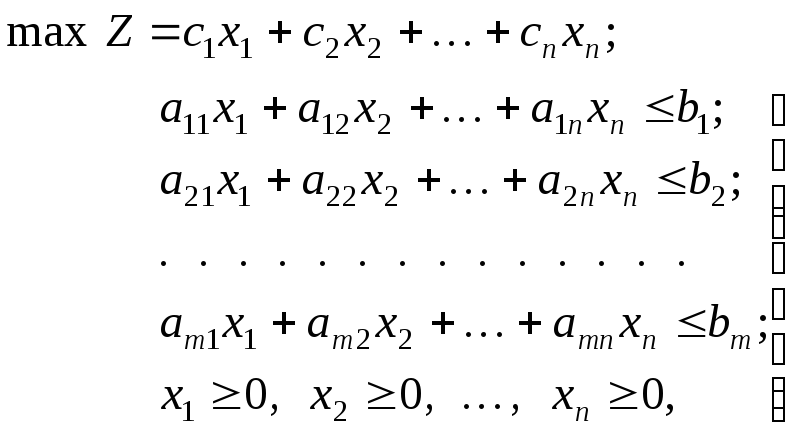где Z – суммарная прибыль;

– объемы выпуска продукции;

– прибыль от производства единицы j-го вида продукции;

– расход i-го ресурса на единицу j-й продукции;

–объемы используемых ресурсов.

Предположим, что на ресурсы есть покупатель, тогда естественно задаться вопросом, какие обстоятельства необходимо учесть при продаже этих ресурсов. Если искомые цены ресурсов обозначить как , а затраты покупателя величиной , то его интересы будут учтены, если за функционал принять

.

С другой стороны, чтобы не снижать доходы при продаже ресурсов, выручка при их продаже должна быть не меньше, чем прибыль от их использования в собственном производстве. Так как затраты ресурсов на производство единицы первого вида продукции определяются первым столбцом матрицы коэффициентов прямой задачи, то должно выполняться условие

,

где – прибыль от производства единицы первого вида продукции. Очевидно, что аналогичные условия должны выполняться и для других возможных видов продукции. Следовательно, модель двойственной задачи будет:

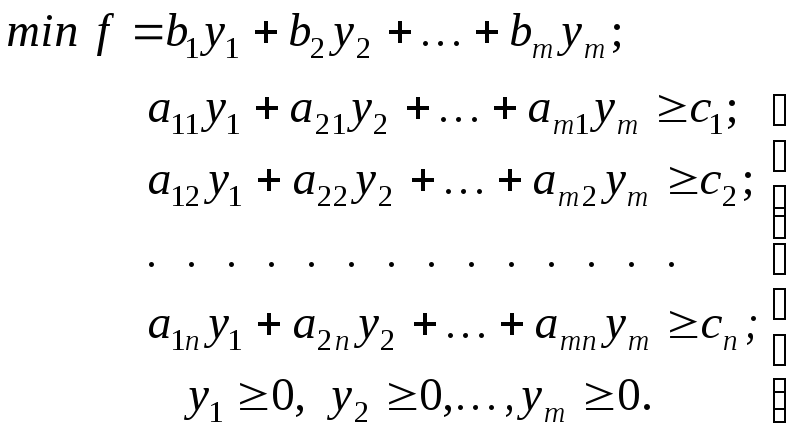
Условие неотрицательности цен очевидно для данной постановки задачи.

Обе рассмотренные задачи имеют симметричную форму, поэтому их принято называть парой симметричных двойственных задач. Действительно, если за прямую принять задачу об оптимальных ценах на сырье, то в качестве двойственной получится задача об оптимальном производственном плане.

Значение расчета цен ресурсов состоит отнюдь не в обосновании целесообразности их продажи, а в оценке их использования и влияния на объем и эффективность производства. Поэтому переменные называют двойственными оценками, или объективно обусловленными оценками. В зарубежной литературе их обычно называют теневыми ценами.

Очевидно, что эти цены определяются эффективностью собственного производства. Если в качестве условного примера представить себе некоторый регион, богатый лесом, но не располагающий возможностями для его переработки, то можно смело предполагать, что продаваться этот лес будет дешево. При развитии собственной лесопереработки цены на продажу леса сразу возрастут.

Рассмотренную пару взаимно двойственных симметричных задач для удобства их сопоставления можно записать в виде конечных сумм:

прямая задача двойственная задача

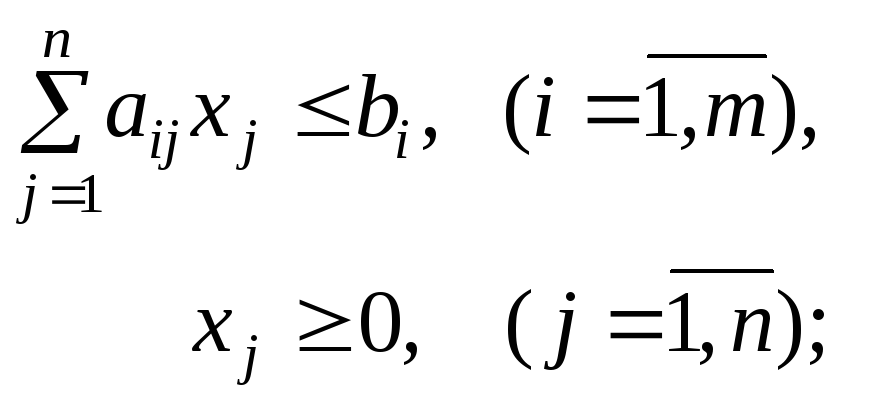
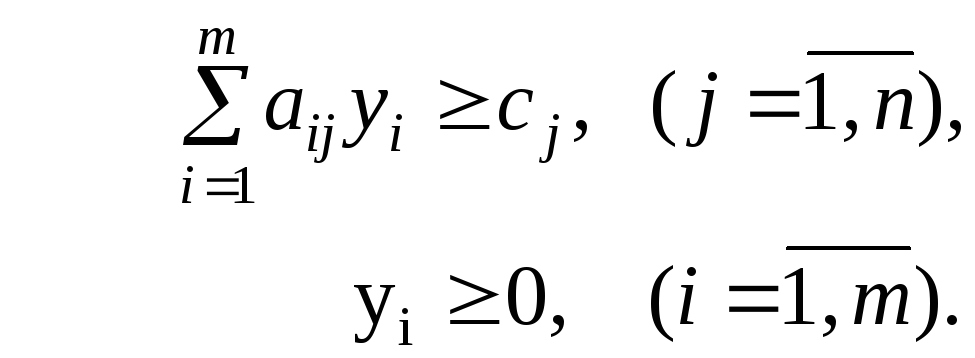
Правила перехода удобно представить графически, используя таблицу, аналогичную симплексной (см. табл. 3.1). Эти правила можно сформулировать так:

1. Если прямая задача – на максимум, то двойственная – на минимум, и наоборот.

2. Каждому из m ограничений прямой задачи соответствует переменная двойственной задачи.

3. Каждой из n переменных прямой задачи соответствует ограничение двойственной.

4. Коэффициенты целевой функции прямой задачи являются свободными членами ограничений двойственной.

5. Свободные члены ограничений прямой задачи являются коэффициентами целевой функции двойственной.

6. Матрица коэффициентов ограничений двойственной задачи получается транспонированием матрицы коэффициентов прямой задачи, и наоборот.

7. Для пары взаимно-двойственных симметричных задач все переменные неотрицательны; задаче на максимум соответствуют неравенства типа , а задаче на минимум – вида .

Таблица 3.1

			…		…
			…		…
			…		…
			…		…
…	…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…	…
			…		…

В качестве примера запишем для уже решенной симплекс-методом модели задачи об оптимальном производственном плане соответствующую математическую модель двойственной задачи

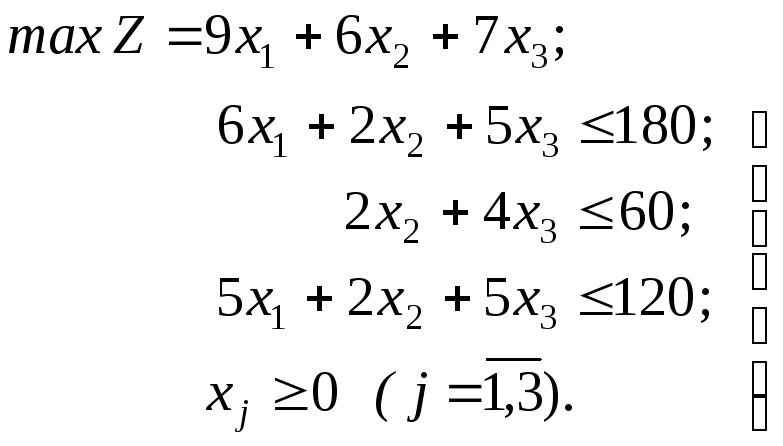
Переменными в ней будут теневые цены ресурсов, а модель согласно приведенным правилам примет вид: