
- •2.2. Формы записи задачи линейного программирования
- •2.3. Приведение задачи линейного программирования к канонической форме
- •2.4. Графическое построение области допустимых решений
- •2.5. Графическое нахождение оптимального решения
- •2.6. Графический анализ чувствительности
- •2.7. Теорема об экстремальном значении целевой функции на выпуклом множестве
Обычно построение
модели начинают с определения ее
переменных. В рассматриваемой задаче
за переменные естественно принять
объемы выпуска каждого из возможных
видов продукции, которые традиционно
обозначают
![]() ,
где
,
где
![]() .
.
Будем искать такой
план выпуска продукции, который обеспечит
максимальную прибыль Z.
Это наиболее часто используемая, хотя
далеко не единственная, трактовка
поставленной задачи. Но преимущество
математического подхода в том и состоит,
что обеспечивается точность всех
формулировок. В данном случае достаточно
знать прибыль от производства единицы
каждого вида продукции, которую обозначим
![]() ,
где
,
где
![]() .
Тогда получаем задачу:
.
Тогда получаем задачу:
Максимизировать
![]() .
.
Осталось сформулировать ограничения, которые состоят в том, что:
 .
.
Для записи этих ограничений необходимо знать коэффициенты затрат ресурсов на производство единицы каждого вида продукции, которые удобно представить в табличной форме. Чтобы сгруппировать все используемые данные, занесем в эту таблицу и коэффициенты целевой функции.
Таблица 2.1
|
Вид ресурса, i |
Расход i-го ресурса на единицу j-й продукции, aij |
Запас ресурса, bi |
||||
|
1 |
2 |
… |
n |
|
||
|
1 |
a11 |
a12 |
… |
a1n |
b1 |
|
|
2 |
a21 |
a22 |
… |
a2n |
b2 |
|
|
… |
… |
… |
… |
… |
… |
|
|
m |
am1 |
am2 |
… |
amn |
bm |
|
|
Прибыль, cj |
c1 |
c2 |
… |
cn |
|
|
Математическая модель задачи примет вид:
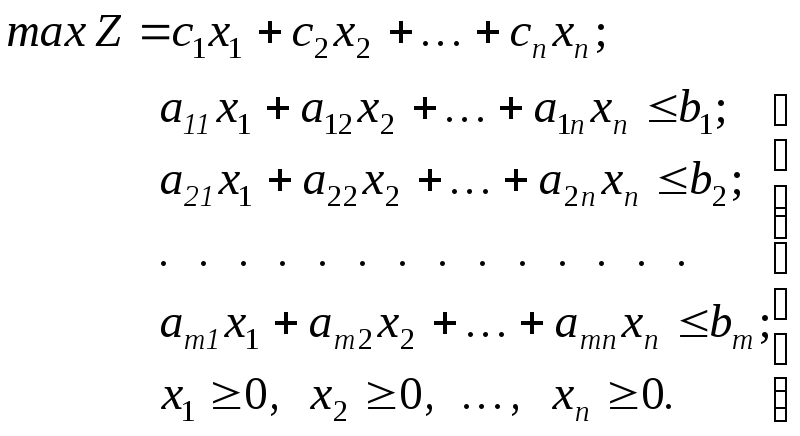
Дополнительно введенные условия неотрицательности переменных очевидным образом определяются экономическим смыслом задачи, но если их не задать при обращении к используемому пакету прикладных программ, то весьма вероятно, что решение не будет получено. Действительно, предположим, что один из видов продукции, требующий расхода всех видов ресурсов, дает весьма незначительную прибыль. Если соответствующей переменной формально придать отрицательное значение, то получим прирост всех ресурсов при малых затратах (соответствующие слагаемые при переносе в правую часть получат знак плюс). Тогда прибыль будет неограниченно возрастать за счет увеличения производства более выгодных видов продукции.
Следует заметить, что при решении реальных экономических задач приведенные выше ресурсные ограничения надо будет дополнять условиями, учитывающими ограниченные возможности реализации продукции и имеющиеся обязательства по ее поставке, взаимосвязи между отдельными видами продукции и т. д. Поэтому процесс построения хорошей модели и является искусством, требующим знания предметной области и ясного экономического мышления.
Задача 2. Формирование минимальной продовольственной корзины. Эту задачу часто называют задачей о рационе. Пусть определен ассортимент продуктов и известны их характеристики (цена; калорийность; содержание белков, жиров, углеводов, витаминов). Требуется найти набор минимальной стоимости, обеспечивающий формирование минимальной продовольственной корзины.
Введем обозначения:
n – число рассматриваемых продуктов;
m – количество учитываемых веществ (в т. ч. калорий);
![]() –
содержание i-го
вещества в j-м продукте,
(
–
содержание i-го
вещества в j-м продукте,
(![]() );
);
![]() ;
;
![]() – потребность
человека в i-м веществе,
– потребность
человека в i-м веществе,
![]() ;
;
![]() –
стоимость единицы
j-го продукта,
–
стоимость единицы
j-го продукта,
![]()
![]() –
количество j-го
продукта в решении,
–
количество j-го
продукта в решении,
![]() .
.
Получим модель, симметричную по отношению к ранее записанной. Только вместо максимума теперь нужно найти минимум, изменились и знаки ограничений
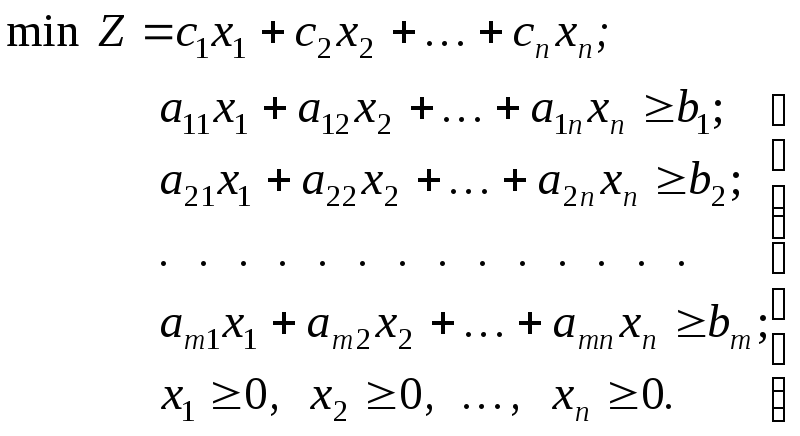
Разумеется, и в этом случае может потребоваться введение определенных соотношений между отдельными группами продуктов, ограничение содержания некоторых ингредиентов и т. д.
2.2. Формы записи задачи линейного программирования
Общая форма задачи линейного программирования. Так называют задачу найти
![]()
при ограничениях
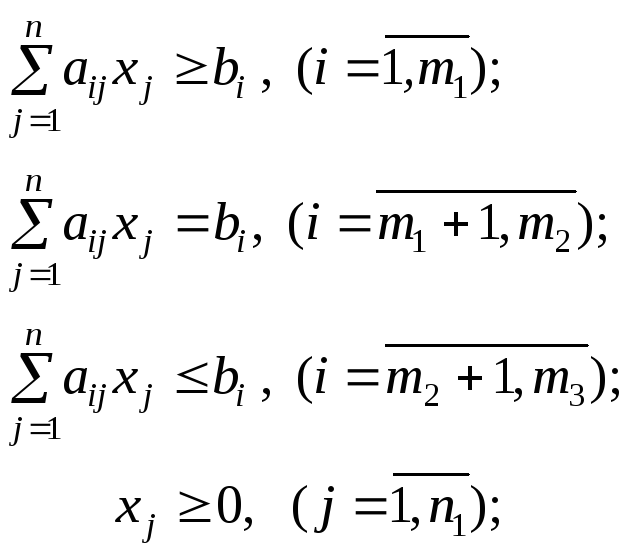 x
j – любого
знака
x
j – любого
знака
![]() .
.
Симметричная форма задачи линейного программирования. Примеры таких задач уже приведены в предыдущем параграфе. Это
![]() ;
;
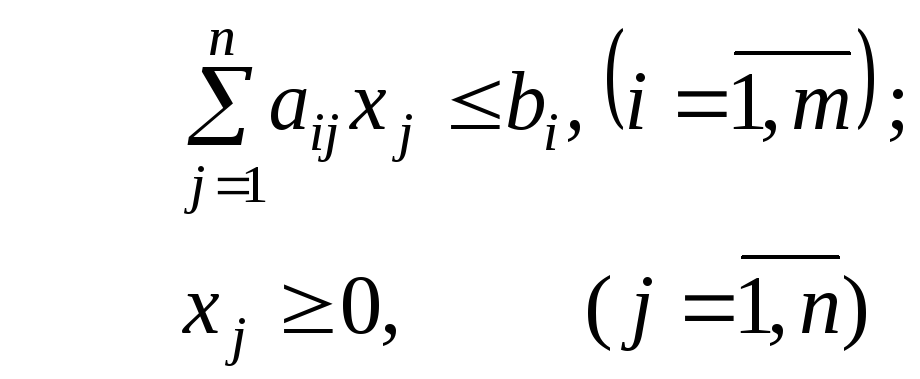
или
![]()
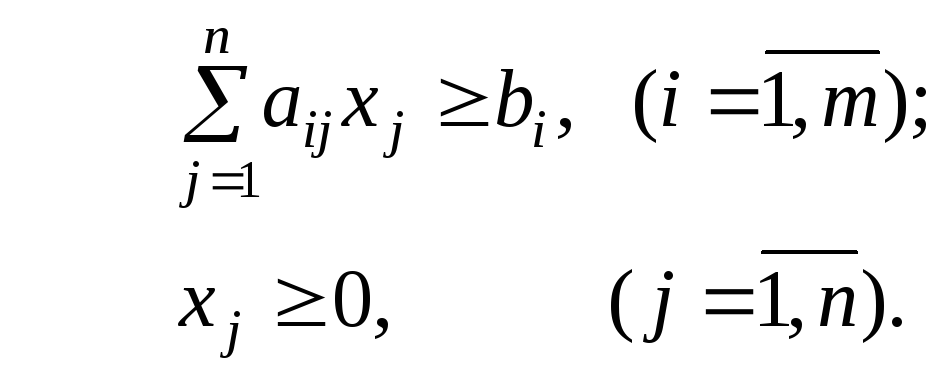
Каноническая форма задачи линейного программирования используется, чтобы применить аппарат линейной алгебры для решения оптимизационных задач. Предполагается, что задача решается только на максимум и что все условия записаны как равенства
![]()
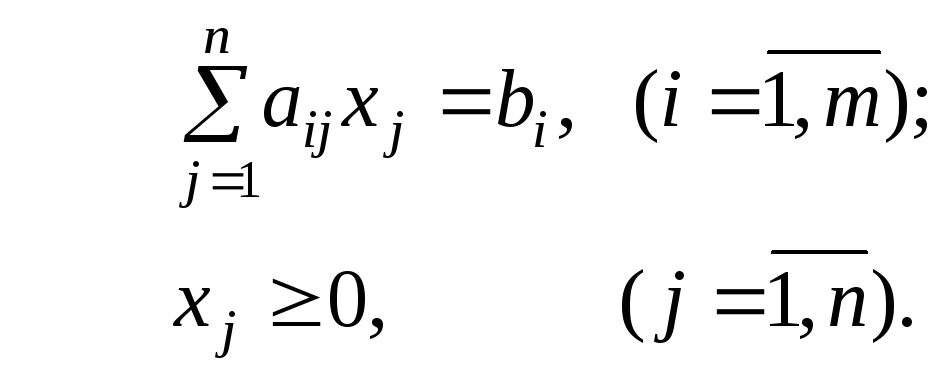
Если ввести обозначения:
![]() – матрица-строка
коэффициентов целевой функции;
– матрица-строка
коэффициентов целевой функции;
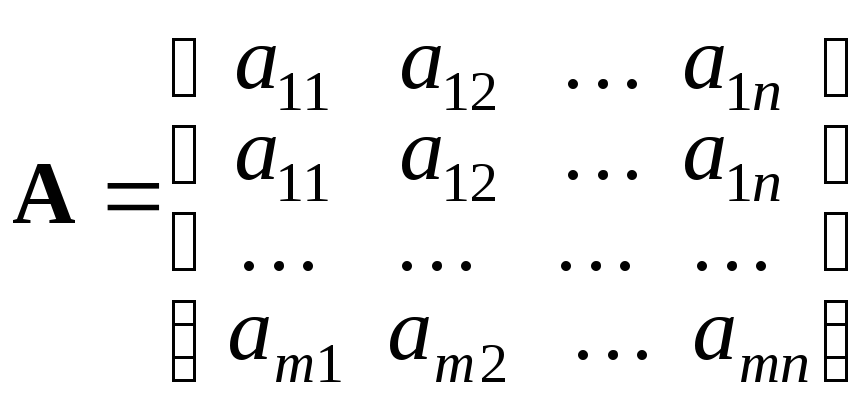 – матрица системы
уравнений;
– матрица системы
уравнений;
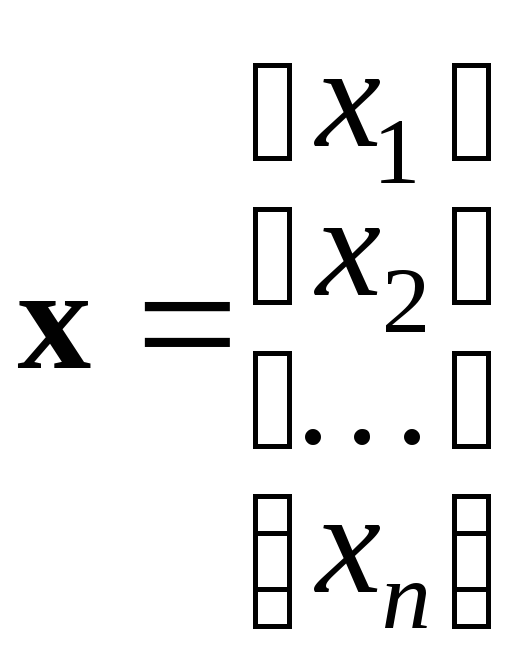 – матрица-столбец
переменных;
– матрица-столбец
переменных;
 – матрица-столбец
свободных членов,
– матрица-столбец
свободных членов,
то каноническая форма задачи в матричной записи примет вид:
![]() ;
;
![]() ,
,
где
cx – скалярное
произведение векторов
![]() и
и
![]() .
.
Используется и векторная форма записи. Если обозначить:
 ,
,
 ,
… ,
,
… ,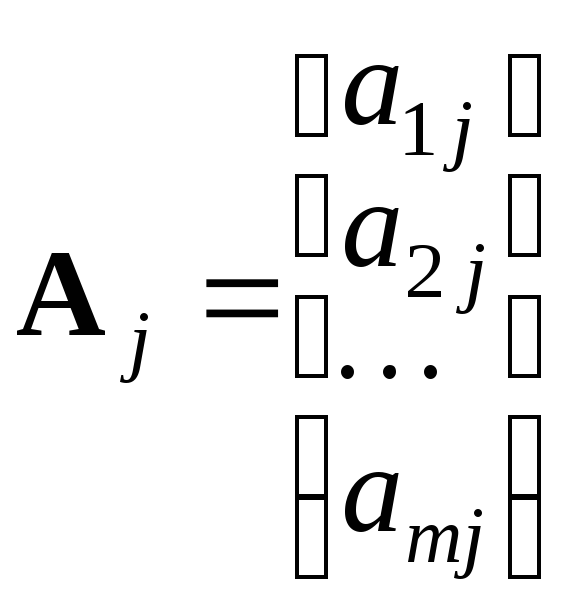 ,
… ,
,
… ,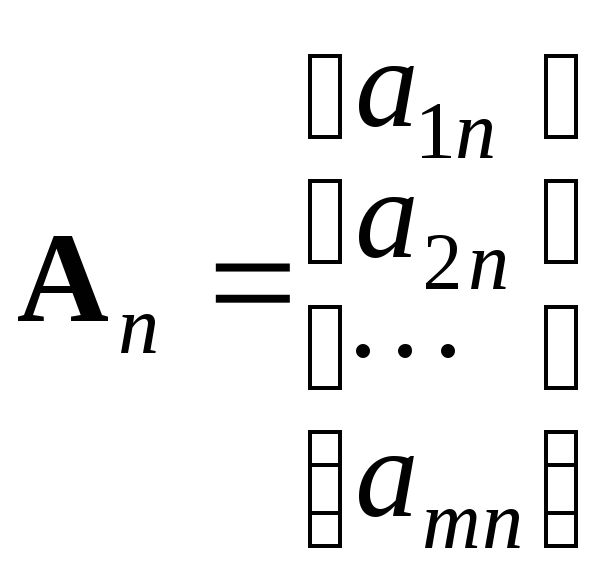 ,
,
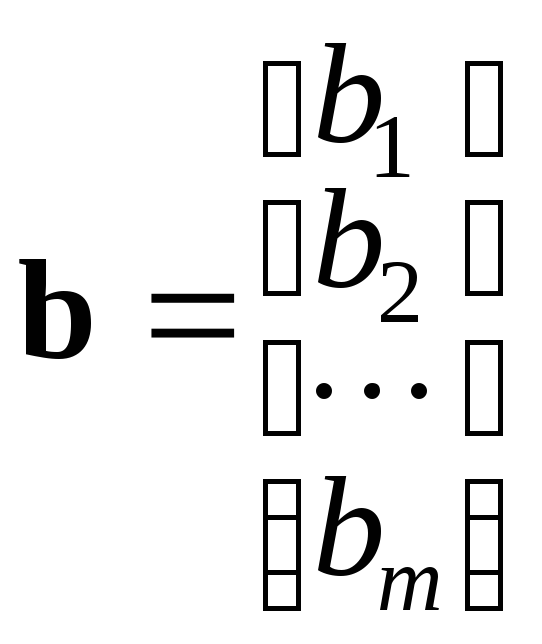 ,
,
то получим:
![]()
![]()
2.3. Приведение задачи линейного программирования к канонической форме
Каноническая форма введена для обоснования метода поиска оптимального решения, но экономические задачи первоначально записываются в общей или симметричной форме. Покажем, что путем эквивалентных преобразований всегда можно перейти к канонической форме.
Преобразование целевой функции. Задачу поиска минимума легко заменить задачей поиска максимума. Если x* – точка минимума функции
![]() ,
то для функции
,
то для функции
![]() она будет точкой максимума.
она будет точкой максимума.
Очевидно, что поиск максимума можно заменить поиском минимума и что эти утверждения справедливы и для функции n переменных:
![]() .
.
x
![]() 0
0
Рис. 2.1
Замена неравенства
типа «меньше или равно» на равенство.
Для каждого ограничения типа
![]() введем свою дополнительную неотрицательную
переменную
введем свою дополнительную неотрицательную
переменную
![]() .
Если вектор x
.
Если вектор x![]() удовлетворяет исходному ограничению,
то всегда можно подобрать ее значение
так, чтобы выполнялось равенство
удовлетворяет исходному ограничению,
то всегда можно подобрать ее значение
так, чтобы выполнялось равенство
![]()
Если это равенство
выполняется при некотором неотрицательном
![]() ,
то будет выполняться и рассматриваемое
ограничение.
,
то будет выполняться и рассматриваемое
ограничение.
Ограничения типа «меньше или равно» были использованы при построении модели оптимального планирования производства. Заменяя их равенствами, получим:
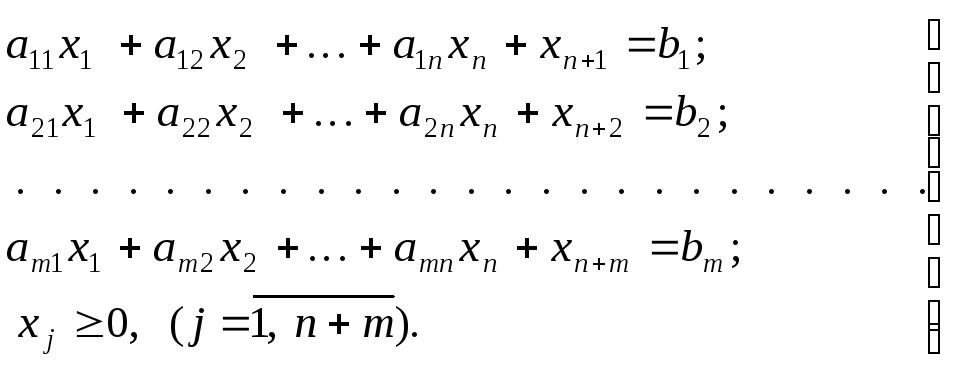
Эти условия часто
называют «ограничения-равенства», так
как равенствами они являются только по
форме, а по содержанию – ресурсными
ограничениями. Каждое из них содержит
свою дополнительную переменную
![]() ,
где (
,
где (![]() ).
Иногда такие переменные называют
остаточными, поскольку их значения
показывают величины неиспользованных
ресурсов. Если продажа (сдача в аренду)
свободных ресурсов не предполагается,
то в целевую функцию модели дополнительные
переменные войдут с нулевыми коэффициентами,
иначе говоря, функционал не изменится.
).
Иногда такие переменные называют
остаточными, поскольку их значения
показывают величины неиспользованных
ресурсов. Если продажа (сдача в аренду)
свободных ресурсов не предполагается,
то в целевую функцию модели дополнительные
переменные войдут с нулевыми коэффициентами,
иначе говоря, функционал не изменится.
Замена неравенства
типа «больше или равно» на равенство
выполняется аналогично. От левой
части каждого ограничения типа
![]() отнимем дополнительную неотрицательную
переменную
отнимем дополнительную неотрицательную
переменную
![]() ,
чтобы обеспечить выполнение равенства
,
чтобы обеспечить выполнение равенства
![]() Если это равенство выполняется при
некотором неотрицательном
Если это равенство выполняется при
некотором неотрицательном
![]() ,
то выполняется и исходное ограничение.
Такие ограничения были использованы
для построения модели формирования
минимальной продовольственной корзины.
После замены неравенства «больше или
равно» равенством получим:
,
то выполняется и исходное ограничение.
Такие ограничения были использованы
для построения модели формирования
минимальной продовольственной корзины.
После замены неравенства «больше или
равно» равенством получим:

В этой модели содержательный смысл дополнительных переменных в том, что они показывают превышение содержания отдельных веществ в рационе сверх заданных минимальных величин. Поэтому их иногда называют избыточными. Очевидно, что в целевую функцию модели они войдут с нулевыми коэффициентами. При расчете подобной модели обеспечение норм по белкам и витаминам приведет, вероятно, к избыточной насыщенности.
Замена переменных
любого знака на неотрицательные
выполняется путем замещения их
разностью неотрицательных переменных.
Действительно, такую переменную
![]() можно представить как
можно представить как
![]() ,
где
,
где
![]() и
и
![]() неотрицательные переменные.
неотрицательные переменные.
Итак, доказано,
что от любой формы записи линейной
модели можно перейти к канонической
форме. Справедливо и обратное, равенство
эквивалентно двум неравенствам с
противоположными знаками:
![]() равносильно
равносильно
![]() и
и
![]() .
.
