
5. Задача нелинейного программирования
5.1. Постановка задачи и основные понятия
Для учета взаимосвязей между переменными и исходными данными задачи далеко не всегда можно ограничиться одними линейными зависимостями. Если функция непрерывна и дифференцируема (а для реальных зависимостей в экономических задачах это, как правило, справедливо), то в малой окрестности рассматриваемой точки приращение функции можно с достаточной точностью заменить дифференциалом, т. е. линейной частью приращения. Линейные модели рассчитывать проще, но не всегда можно предполагать, что область изменения переменных достаточно мала, чтобы только линейные зависимости позволили обеспечить адекватность модели.
Например, при увеличении производственной
программы возможно увеличение процента
брака, увеличение затрат на оплату
сверхурочных работ, на хранение продукции
и т. п., следовательно, нормы расхода
ресурсов на единицу выпускаемой продукции
и прибыль необходимо рассматривать как
функции от объемов выпуска продукции.
Если эти функции даже предполагать
линейными, и обозначить
![]() – объем производства j-й продукции,
то нормы расхода ресурсов на единицу
этой продукции и прибыль будут определяться
выражениями
– объем производства j-й продукции,
то нормы расхода ресурсов на единицу
этой продукции и прибыль будут определяться
выражениями
![]() и
и
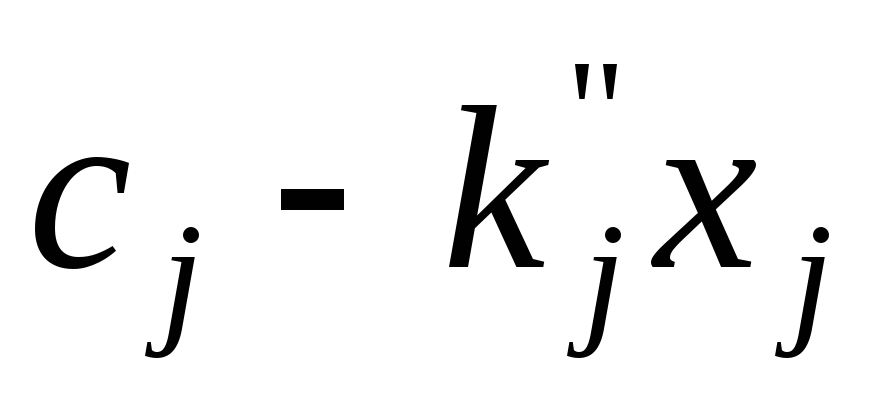 .
При подстановке этих выражений в
ограничения и целевую функцию исходной
линейной модели получим слагаемые вида
.
При подстановке этих выражений в
ограничения и целевую функцию исходной
линейной модели получим слагаемые вида
![]() и
и
 соответственно. Теперь и ограничения,
и функционал задачи стали нелинейными,
так как содержат неизвестные во второй
степени.
соответственно. Теперь и ограничения,
и функционал задачи стали нелинейными,
так как содержат неизвестные во второй
степени.
В общем случае задача нелинейного
программирования состоит в определении
точки
![]() ,
обеспечивающей экстремум (максимум,
либо минимум) функции
,
обеспечивающей экстремум (максимум,
либо минимум) функции
![]() и удовлетворяющей заданным ограничениям
вида
и удовлетворяющей заданным ограничениям
вида
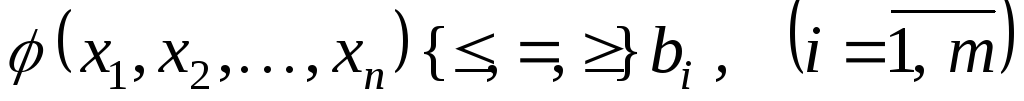 .
Нелинейность любой из этих функций
влечет существенные отличия от задачи
линейного программирования. Для случая
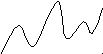
одной переменной ясно (см.
рис.
5.1), что экстремум может достигаться не
только на границе области, как это было
в задаче линейного программирования,
но и внутри области допустимых решений.
Так функция f1
(x)
наименьшее значение принимает в точке
a на границе области (a, b), но
ее максимум достигается во внутренней
точке области x*. Более того,
экстремальных точек может быть несколько,
поэтому говорят о локальных и глобальных
экстремумах. Так, функция f2
(x) кроме
глобального максимума в точке x*имеет
локальные максимумы в точках x′ и
x″.
.
Нелинейность любой из этих функций
влечет существенные отличия от задачи
линейного программирования. Для случая
одной переменной ясно (см.
рис.
5.1), что экстремум может достигаться не
только на границе области, как это было
в задаче линейного программирования,
но и внутри области допустимых решений.
Так функция f1
(x)
наименьшее значение принимает в точке
a на границе области (a, b), но
ее максимум достигается во внутренней
точке области x*. Более того,
экстремальных точек может быть несколько,
поэтому говорят о локальных и глобальных
экстремумах. Так, функция f2
(x) кроме
глобального максимума в точке x*имеет
локальные максимумы в точках x′ и
x″.
f1
(x)
f2
(x)

x x a b a b x′ x″
x*
x*

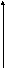









Рис. 5.1
При нелинейных ограничениях область допустимых решений может быть любой и даже состоять из несвязанных между собой частей (рис. 5.2).

Рис. 5.2
Поэтому не существует общего метода для решения задач нелинейного программирования, подобного симплексному методу для решения задач линейной оптимизации. Однако отдельные типы задач достаточно хорошо изучены. Следует выделить классические задачи оптимизации, когда все ограничения заданы как равенства, число ограничений меньше числа переменных, отсутствуют условия неотрицательности или дискретности переменных, целевая функция и функции ограничений непрерывны и имеют частные производные первого и второго порядка. Для таких задач используется метод множителей Лагранжа, являющийся теоретической основой почти всех задач нелинейной оптимизации.
Важный класс задач математического программирования (его условия выполняются для большинства экономических приложений) – это задачи выпуклого программирования, для которых область допустимых решений является выпуклой и целевая функция также выпукла (вогнута). Такие задачи эффективно решаются градиентными методами, однако сначала надо дать определение понятию выпуклой функции.
Функция
![]() ,
определенная на выпуклом множестве
,
определенная на выпуклом множестве
![]() ,
называется выпуклой, если для любых
двух точек x′ и
x″ из этого
множества справедливо неравенство
,
называется выпуклой, если для любых
двух точек x′ и
x″ из этого
множества справедливо неравенство
![]() ,
где
,
где
![]() .
.
Геометрически это означает, что все точки отрезка, соединяющего две любые точки поверхности, которую задает выпуклая функция, лежат на этой поверхности или выше ее (рис. 5.3).
Если неравенство является строгим, т. е.
![]() при
при
![]() ,
,
то говорят, что
![]() строго выпуклая функция. Для вогнутой
функции знак неравенства меняется на
обратный. Линейная функция одновременно
является выпуклой и вогнутой.
строго выпуклая функция. Для вогнутой
функции знак неравенства меняется на
обратный. Линейная функция одновременно
является выпуклой и вогнутой.
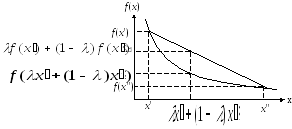
Рис. 5.3
В качестве основной задачи в теории
выпуклого программирования обычно
рассматривается задача минимизации
выпуклой функции n
переменных
![]() при ограничениях
при ограничениях
![]() ,
,
![]()
![]() ,
где функции
,
где функции
![]() также выпуклые. Поскольку x
– это вектор
также выпуклые. Поскольку x
– это вектор
![]() ,
то запись
,
то запись
![]() означает условие неотрицательности
его координат. Для этой задачи можно
доказать, что область допустимых планов
выпукла и что локальный минимум совпадает
с глобальным минимумом.
означает условие неотрицательности
его координат. Для этой задачи можно
доказать, что область допустимых планов
выпукла и что локальный минимум совпадает
с глобальным минимумом.
Для проверки функции на выпуклость
используется критерий Сильвестра:
функция![]() будет выпуклой, если ее вторые частные
производные
образуют матрицу, в которой все главные
миноры (миноры, расположенные
в левом верхнем углу) неотрицательны.
будет выпуклой, если ее вторые частные
производные
образуют матрицу, в которой все главные
миноры (миноры, расположенные
в левом верхнем углу) неотрицательны.
Самым простым подходом к решению задачи нелинейного программирования (хотя отнюдь не лучшим) будет перебор возможных значений переменных, удовлетворяющих заданным ограничениям с расчетом значений функционала и запоминанием лучших вариантов. Для организации такого перебора часто используется случайный поиск. При использовании современной вычислительной техники и умеренной размерности задачи вполне можно приблизиться к оптимальному решению или, по крайней мере, найти начальное приближение для использования других методов.
