4. Целочисленное программирование

4.1. Основные понятия целочисленного программирования

При решении реальных экономических задач часто оказывается, что все или некоторые из искомых переменных могут принимать только вполне определенные значения. Например, если при ограниченных средствах для инвестиций приходится выбирать отдельные проекты из целого ряда возможных, то по отношению к каждому проекту решение может быть только типа «да-нет». Для построения модели такой задачи естественно ввести двоичные переменные :

Если при расчете оптимального числа торговых точек получится значение 2,7, то в модель, очевидно, следует ввести требование целочисленности соответствующей переменной. Однако если расчет оптимальной численности поголовья скота даст величину 801,5, то этот результат можно просто округлить.

Иногда приходится выбирать одно значение из некоторого набора дискретных величин, которые не обязательно являются целыми. Пусть надо выбрать автомобиль подходящей грузоподъемности или рациональный объем морозильной камеры. Ряд авторов считает более правильным использовать в таких случаях термин дискретное программирование.

Чтобы пояснить возникающие при решении таких задач проблемы рассмотрим случай, когда нужно найти оптимальные значения двух целых положительных переменных по критерию , если область допустимых решений определяется следующими двумя ограничениями ресурсного типа. Граница первого ограничения (см. рис. 4.1) это прямая PA, второго – прямая AQ, где координаты точек следующие:

P(0; 5,1), A(3,2; 4,825), Q(4,1; 0).

Если перемещать прямую перпендикулярную вектору градиента с учетом требования, что она должна проходить через одну из допустимых точек с целочисленными координатами, то видно, что искомый максимум достигается в точке В(1; 5).

Однако при большем числе переменных необходимо использовать аналитические методы решения. Представляется логичным взять за основу оптимальное решение, которое можно получить симплексным методом, если не учитывать требование целочисленности. Тогда для рассматриваемого примера получим в точке A(3,2; 4,825).

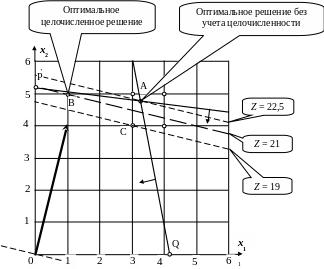
Рис. 4.1

При разных вариантах округления координат точки A до целых значений только точка C(3; 4) удовлетворяет ограничениям. Но значение функционала в этой точке , что меньше полученного в точке B.

На основе проведенного анализа можно сделать следующие выводы:

1. Округление в любую сторону решения, полученного без учета требования целочисленности, может привести к выходу за пределы области допустимых решений.

2. Оптимальным решением целочисленной задачи может оказаться такое решение, в котором значения переменных значительно отличаются от значений, полученных при решении непрерывной задачи.

4.2. Методы решения задач целочисленного программирования

Объективная сложность рассматриваемой задачи повлекла развитие различных методов ее решения, среди которых можно выделить две основные группы: точные и приближенные. Точные алгоритмы, как правило, предусматривают:

1. Расширение области допустимых решений путем отбрасывания требования целочисленности. При этом для непрерывных переменных, заменяющих двоичные переменные, вводится ограничение

2. Решение задачи линейного программирования.

3. Если полученный оптимальный план удовлетворяет всем ограничениям исходной целочисленной задачи, то она решена и расчет завершен, иначе, переходим к следующему этапу.

4. Добавление специального ограничения (или ограничений) так, чтобы уменьшить область допустимых решений, но не исключить при этом искомое оптимальное целочисленное решение. Далее повторяются три последних этапа.

Для построения специальных ограничений известны два общих метода:

1. Метод ветвей и границ.

2. Метод отсечения.

Следует отметить, что ни один из них не гарантирует решения конкретной задачи, а реальные границы применимости того или иного метода определяются как алгоритмом его реализации, так и возможностями используемой вычислительной техники. Поэтому при появлении проблем с выполнением расчетов разумно переходить к использованию новых версий специализированных пакетов прикладных программ, так как их разработчики сразу могли ориентироваться на более мощные компьютеры и реализовывать более эффективные алгоритмы.

Поскольку технические проблемы решения определяются прежде всего числом целочисленных переменных, то желательно по возможности заменять их непрерывными, а если их необходимо использовать, то ограничивать диапазоны их изменения.

Так как оптимизация целочисленных задач требует выполнения значительного объема вычислений, то ограничимся рассмотрением сути этих методов.

Метод ветвей и границ.

Этот метод считается наиболее эффективным. Он относится к группе комбинаторных методов и основан на разбиении множества всех допустимых планов исходной задачи на конечное число непересекающихся подмножеств и определении для них оценок максимально-возможного значения функционала (предполагается, что исходная задача решается на максимум). Если процесс такого ветвления продолжать разумным образом и для очередного шага ветвления выбирать подмножество с максимальной оценкой, как наиболее перспективное, то после получения решения, удовлетворяющего требованиям целочисленности, ветвление нужно будет продолжать только для тех подмножеств оценки, для которых превышают уже достигнутый результат.

Для разбиения на подмножества выберем одну из переменных, которая должна быть целочисленной, но после решения без учета требования целочисленности таковой не является. Для задачи, решенной выше графическим способом, выберем, например, и разобьем пространство допустимых решений исходной задачи без учета требования целочисленности на три подмножества:

1. Пространство допустимых решений исходной задачи с дополнительным условием .

2. Пространство допустимых решений исходной задачи с дополнительным условием .

3. Пространство допустимых решений исходной задачи с дополнительным условием

Последнюю задачу из дальнейшего рассмотрения можно исключить, как не содержащую целочисленных решений переменной , а при решении двух первых симплексным методом без учета требования целочисленности получим (графически это очевидно):

1. , , Z = 21.

2. , , Z = 19,354.

Первая подзадача имеет целочисленное решение, лучшего она содержать не может, поэтому про такую задачу говорят, что она прозондирована. Любое возможное целочисленное решение второй подзадачи не может быть лучше уже полученного, следовательно, ее можно считать прозондированной и отбросить.

В реальных задачах процесс ветвления может потребовать значительного количества шагов. Даже в приведенном простом примере, если за переменную ветвления взять не , а , то целочисленного решения сразу не получится. Строгой теории для выбора переменной ветвления не существует, хотя этот выбор, а также порядок выбора подзадач определяют объем необходимых вычислений.

Метод отсечения.

Этот метод по имени автора часто называют алгоритмом Гомори. Основной вариант алгоритма предполагает, что требование целочисленности относится ко всем переменным модели. Как и в методе ветвей и границ сначала исходная задача решается без учета этого требования. Если полученное решение не является целочисленным, то вводится дополнительное ограничение (отсекающая плоскость), которое:

1. Отсекает часть области допустимых решений, содержащую найденное оптимальное (но не целочисленное) решение.

2. Не содержит ни одного допустимого целочисленного решения поставленной задачи.

3. Проходит хотя бы через одну целочисленную точку (допустимую или недопустимую).

Повторно применяется симплексная процедура к задаче с расширенной системой ограничений и если решение не окажется целочисленным, то процесс повторяется. После некоторого числа отсечений искомая целочисленная точка окажется сначала на границе, а в дальнейшем станет оптимальным решением, если хоть одно допустимое решение исходной задачи существует.