5.2. Графоаналитический метод

Если область допустимых значений переменных изобразить в виде некоторого множества на плоскости и нанести линии, соответствующие фиксированным значениям функционала, то можно графически найти искомое оптимальное решение. Найдем максимум функции (см. рис. 5.4)

→ max

при ограничениях

Если построить несколько линий, соответствующих фиксированным значениям функционала, то можно подобрать такое значение Z, что построенная кривая будет касаться выделенного многоугольника в некоторой точке x^*. Очевидно, что в этой точке и достигается искомый максимум.

x₂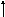

x₁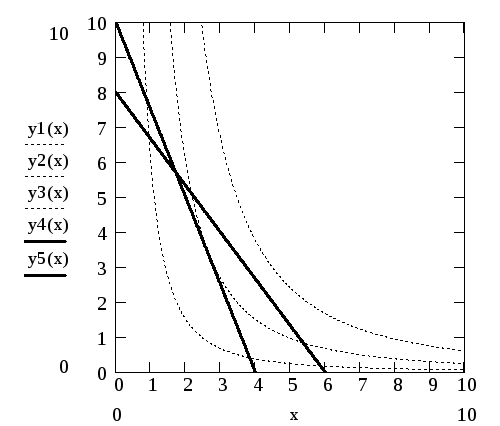

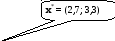
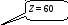
Рис. 5.4

Точное построение необходимых линий (особенно кривых) весьма трудоемко, но довольно просто выяснить, какое из заданных ограничений определит искомую точку экстремума. В рассматриваемом примере нужно найти максимум функции при условии . Следовательно, и после подстановки в функционал получим . Приравнивая нулю первую производную имеем . Первый корень этого квадратного уравнения обеспечивает функционалу минимум. Сокращая, получим , откуда , и после подстановки . Итак, аналитический расчет обеспечивает уточнение результата, а наглядность, присущая графическому методу, делает его незаменимым для иллюстрации сущности рассматриваемых задач.

5.3. Метод множителей Лагранжа

Рассмотрим классическую задачу оптимизации

.

В этом случае все ограничения являются равенствами, m < n, а рассматриваемые функции предполагаются непрерывными и имеющими частные производные, по крайней мере, второго порядка. Тогда искомые точки экстремума можно найти известным из математического анализа методом множителей Лагранжа. Эти неопределенные множители вводятся для каждого ограничения-равенства. Обозначим их как вектор . Порядок решения задачи методом неопределенных множителей Лагранжа следующий:

1. Составить функцию Лагранжа

.

2. Найти и приравнять нулю частные производные функции Лагранжа

3. Решить полученную систему n+m уравнений, чтобы найти все стационарные точки функции Лагранжа.

4. Выбрать из этих точек, взятых без координат , те, в которых достигается условный экстремум функции . Вычислить соответствующие значения функции, чтобы определить искомый экстремум. Для конкретной задачи такой выбор, как правило, является очевидным.

Если необходимо теоретически обосновать, что стационарная точка действительно является точкой экстремума, то надо исследовать знак второго дифференциала функции Лагранжа в окрестности этой точки. Если , то имеет место условный минимум (любое малое перемещение от стационарной точки приводит к увеличению, как функции , так и функции , поскольку заданные ограничения удовлетворяются). При будет условный максимум.

Рассмотрим как пример задачу об определении оптимального размера партии товара в теории управления запасами. Будем предполагать, что некоторый однородный товар расходуется с постоянной скоростью и годовая потребность в нем составляет S единиц. Пусть затраты на хранение единицы товара в течение всего года составляют , а затраты, связанные с оформлением и доставкой партии товара,– и не зависят от размера партии. Если предполагать, что дефицит не допускается и пополнение запаса происходит мгновенно, то очередная поставка должна производиться в момент полного использования запаса (рис. 5.5).

Рис. 5.5

Обозначим x – размер партии товара, y – число заказываемых партий в течение года. Тогда средняя величина запаса товара равна , суммарные расходы на хранение – , расходы, связанные с оформлением и доставкой заказов, – . Математическая модель задачи имеет вид:

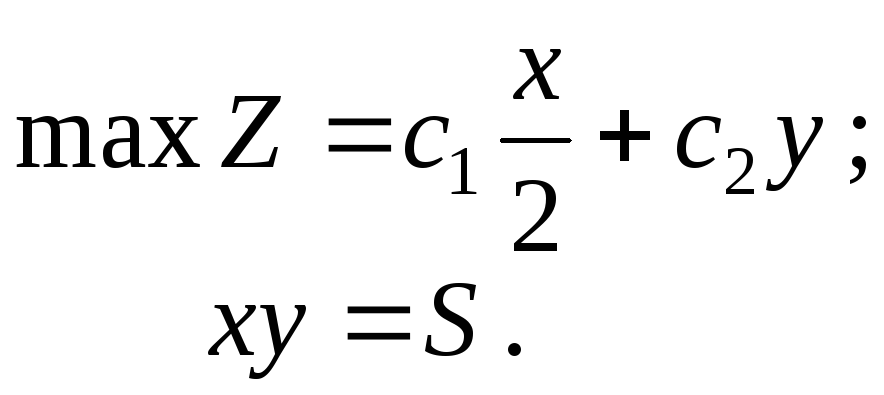
Составляем функцию Лагранжа:

.

Находим и приравниваем к нулю ее частные производные:

Выражая из первых двух уравнений, получим: и ,

следовательно, и .

Подставляя в третье уравнение системы, имеем: , что позволяет определить оптимальный размер партии товара, .

Следует отметить, что цена товара непосредственно не влияет на размер заказываемой партии. Вообще в задачах управления производством элементы суммарных затрат, которые определяются только внешними факторами, не влияют на искомое решение.

Пусть, например, (рис. 5.6) годовая потребность составляет

S = 1000 ед., затраты на хранение  = 2, затраты на оформление и доставку партии товара  = 10. В данном случае оптимальный размер партии будет 100 единиц.

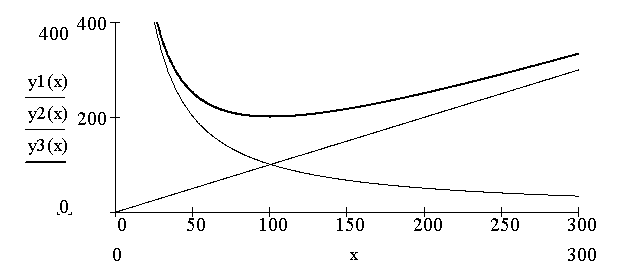
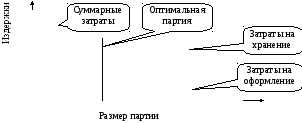
Рис. 5.6