5.6. Теорема Куна-Таккера

В нелинейной оптимизации особую роль играет теорема Куна-Так-кера, которая позволяет распространить метод множителей Лагранжа на задачи, содержащие ограничения-неравенства, и сформулировать для таких задач необходимые условия существования стационарных точек. В частности, для задачи выпуклого программирования: минимизировать выпуклую функцию n переменных при ограничениях , , где функции также выпуклые. Эта теорема устанавливает связь между ее оптимальным решением и седловой точкой функции Лагранжа:

.

Теорема Куна-Таккера. Вектор тогда и только тогда является решением задачи выпуклого программирования, когда существует вектор такой, что при и для любых и выполняется неравенство

и

.

Неравенство означает, что точка является седловой точкой функции Лагранжа, обеспечивая последней минимум по x при фиксированном и максимум по λ при фиксированном (рис. 5.10).

Рис. 5.10

Ограничимся доказательством достаточности приведенных условий. Если подставить в приведенное в качестве условия теоремы неравенство выражение для функции Лагранжа, получим:

.

Левое неравенство можно переписать в виде

, учитывая, что .

Оно будет выполняться при любом неотрицательном , если точке выполняются ограничения , .

Правое неравенство можно переписать как ,

следовательно, для любой точки из области допустимых решений , и точка является точкой глобального минимума.

Если функции и , дифференцируемы, то условия теоремы эквивалентны локальным условиям теоремы Куна-Таккера:

Действительно, если эти условия выполняются, то при фиксированном функция Лагранжа будет выпуклой по x, следовательно, ее приращение будет не меньше произведения ее градиента на приращение аргумента (см. рис. 5.11) –

.

Рис. 5.11

Учитывая второе из локальных условий теоремы Куна-Таккера, получим

.

Поскольку все слагаемые в правой части неотрицательны, то

и правое из неравенств, определяющих седловую точку, доказано. Выполнение левого неравенства можно обосновать аналогично.

5.7. Задача квадратичного программирования

Задачу квадратичного программирования обычно ставят как

при условиях

, .

При этом предполагается, что матрица квадратичной формы

симметрическая и положительно определенная.

Поскольку при записи матрицы квадратичной формы принимается, что , то при транспонировании эта матрица не изменится и поэтому является симметричной. Матрица будет положительно определенной (критерий Сильвестра) если все ее главные миноры положительны. В этом случае соответствующая ей квадратичная форма строго положительна для всех .

Например, квадратичной форме

соответствует матрица

,

главные миноры которой

, ,

положительны. В простых задачах свойства квадратичной формы можно выяснить, исключая парные произведения переменных путем дополнения до полных квадратов. Так, для приведенного примера имеем выражение

,

которое всегда положительно, если хоть один аргумент не равен нулю.

Предположения, относящиеся к квадратичной форме, обеспечивают выпуклость функционала, а поскольку все ограничения линейны, то область допустимых решений также выпукла. Следовательно, задача квадратичного программирования является частным случаем задачи выпуклого программирования и для ее решения можно использовать локальные условия теоремы Куна-Таккера.

Если необходимо найти максимум целевой функции, то достаточно изменить знак функционала на обратный для перехода к поиску минимума и убедиться, что квадратичная форма положительно определена. Если есть ограничения типа , то, умножая их на –1, получим ограничения типа .

Для задачи квадратичного программирования функция Лагранжа это

.

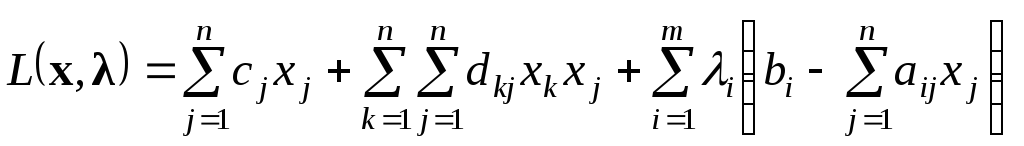Тогда условия теоремы Куна-Таккера примут вид:

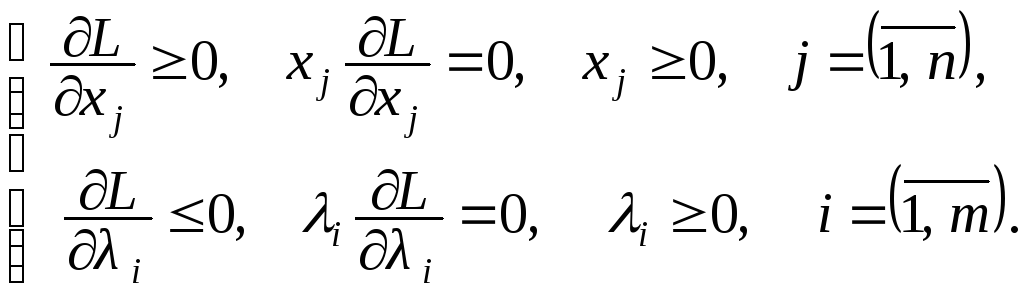
Используемые в локальных условиях теоремы Куна-Таккера частные производные, которые являются линейными функциями, обозначим соответственно

и

,

чтобы свести задачу к решению системы линейных уравнений

Число переменных этой системы в два раза больше числа уравнений, но в соответствии с локальными условиями теоремы Куна-Таккера для того, чтобы решение было оптимальным необходимо и достаточно, чтобы остальные переменные удовлетворяли условиям:

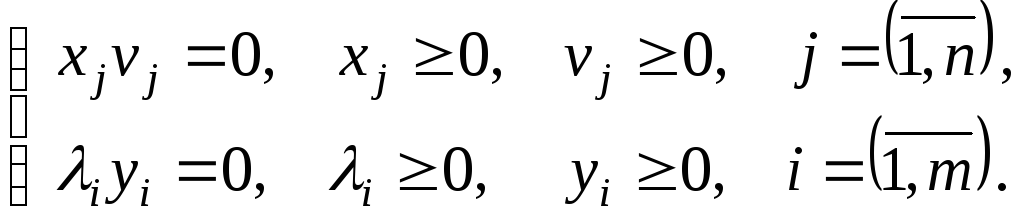
Эти условия можно выполнить только в случае, если, по крайней мере, переменных будут иметь нулевые значения. Но решения линейной системы уравнений, обладающие таким свойством, это ее базисные решения, для перебора которых можно использовать симплексный метод. Если при этом все искусственные переменные будут выведены из базиса, то такое решение и будет оптимальным. Рассмотренная теория позволяет реализовать соответствующее программное обеспечение для эффективного решения задачи квадратичного программирования.

72