2.5. Графическое нахождение оптимального решения

Предположим, что область допустимых решений – непустое множество, содержащее более одной точки. Если множество состоит из одной очки, то оптимизация не требуется, достаточно эту точку найти. В общем же случае необходимо определить в области допустимых решений точку (или точки), в которой функционал приобретает наибольшее или наименьшее значение. Возьмем произвольное фиксированное значение Z=Z₁. Эти значения функционал будет принимать во всех точках некоторой прямой. Если изменить это значение, например, принять Z=Z₂, то прямая, соответствующая новому значению функционала, будет параллельна уже построенной (см. рис. 2.7).

Теперь из семейства параллельных прямых, соответствующих фиксированным значениям функционала, следует выделить те две прямые, при которых достигаются его минимальное и максимальное значения. Эти прямые будут соприкасаться с областью допустимых решений, но не могут ее пересекать. При построении за область допустимых решений принят многоугольник, а линии фиксированных значений функционала изображены пунктиром; принято также, что .

При возрастании значения функционала, прямая, в точках которой эти значения достигаются, будет удаляться от начала координат. Первое соприкосновение с областью допустимых решений произойдет в точке x*_min , последнее в точке x*_max .

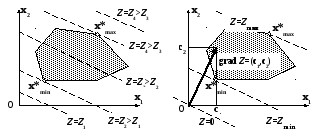
Рис 2.7

Направление наискорейшего возрастания любой дифференцируемой функции определяется вектором градиента, координаты которого есть ее частные производные по всем переменным. Если , то . Для рассматриваемой линейной модели функционал имеет вид и, следовательно, во всех точках плоскости. Отложим вектор градиента из начала координат, тогда, поскольку любая прямая (для которой значения функционала постоянны) перпендикулярна вектору градиента, можно найти координаты искомых экстремумов. При реализации этого способа удобно сначала проводить прямую, перпендикулярную вектору градиента, через начало координат, чтобы не ошибиться в построении прямых, проходящих через точки экстремумов.

Рис. 2.8

Для случая двух переменных очевидно, что одна из угловых точек всегда обеспечит искомый экстремум, если только он существует. Например, когда область допустимых планов неограниченная, можно найти только минимальное значение функционала (см. рис. 2.8). Но экстремум может одновременно достигаться в двух угловых точках (x₁*_max и x₂*_max), тогда во всех точках отрезка, соединяющего эти угловые точки, функционал будет иметь то же самое значение. В этом случае существует бесконечное множество решений.

Очевидно, что решение нельзя найти в случае пустого множества допустимых планов. Нет оснований для оптимизационного подхода и тогда, когда это множество состоит из одной единственной точки. В подобных ситуациях, а они часто возникают на нижних уровнях управления при директивном планировании, необходим пересмотр постановки задачи.

2.6. Графический анализ чувствительности

В действительности исходные данные для модели не только определяются с некоторой погрешностью, но и изменяются по различным причинам. Конечно, всегда можно, изменяя отдельные параметры, рассчитать серию вариантов, чтобы оценить их влияние на оптимальное решение. Такой прием, как правило, полезен на заключительном этапе анализа задачи, но простой перебор вариантов не лучший способ анализа ситуации.

Рассмотрим, основываясь на графическом решении, основные идеи анализа чувствительности. Определим, как влияют изменения величин коэффициентов целевой функции и правых частей ограничений на оптимальное решение. Пусть задана линейная модель следующего вида:

.

При построении удобно нумеровать все заданные ограничения. Тогда легко проверять правильность построения как линий, так и области допустимых решений (см. рис. 2.9).

x₂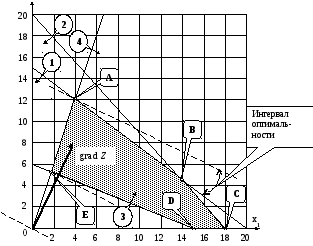

Рис. 2.9

После построения вектора , перемещая перпендикулярную к нему линию фиксированных значений функционала, найдем, что искомые экстремумы достигаются в точках:

A(4; 12), Z_max = 120 и E(1,8; 5,3), Z_min = 49,4.

Очевидно, что эти точки останутся экстремальными и в некотором диапазоне изменения вектора градиента. Изменение модуля этого вектора влечет только пропорциональное изменение величин функционала и не влияет на координаты точек экстремума. Поэтому задача определения чувствительности решения по отношению к коэффициентам целевой функции сводится к определению интервала изменения отношения , для которого остается неизменной рассматриваемая точка экстремума.

Пусть , тогда любое увеличение (уменьшение ) приведет только к повороту вектора градиента против часовой стрелки, что не повлияет на положение точки максимума. Однако как только этот вектор станет перпендикулярен прямой DE (третье ограничение), а это произойдет, если , все точки этого отрезка будут обеспечивать минимальные значения функционалу. Дальнейшее увеличение повлечет перемещение точки минимума в точку D.

Граничное значение отношения легко находится, если вспомнить, что вектор – это перпендикуляр к прямой . Уравнение прямой DE – это , а – это вектор ее нормали. На рисунке показан интервал оптимальности и для точки максимума при возрастании коэффициента . Максимум переместится в точку B как только , а при дальнейшем увеличении этого отношения даже в точку C.

Аналогичный подход можно применить и по отношению ко всем остальным коэффициентам модели. Изменение правых частей ограничений приведет параллельному перемещению соответствующих прямых, изменение коэффициентов при переменных – к изменению углов их наклона. Если прямая определяет точку экстремума, то можно определить зависимость приращения координат этой точки от таких изменений. Например, при уменьшении правой части первого ограничения, эта точка будет плавно перемещаться по отрезку AE.

Такой анализ устойчивости решения важен в реальных экономических задачах, когда необходимо учитывать и погрешности в исходных данных и возможные изменения ситуации. Поэтому современные компьютерные программы предусматривают получение отчетов по устойчивости решения, если только это возможно. Проведенный выше анализ иллюстрирует идею такого подхода.