3.2. Несимметричные двойственные задачи

Реальные задачи записываются в симметричной форме только в простейших случаях, но к канонической форме

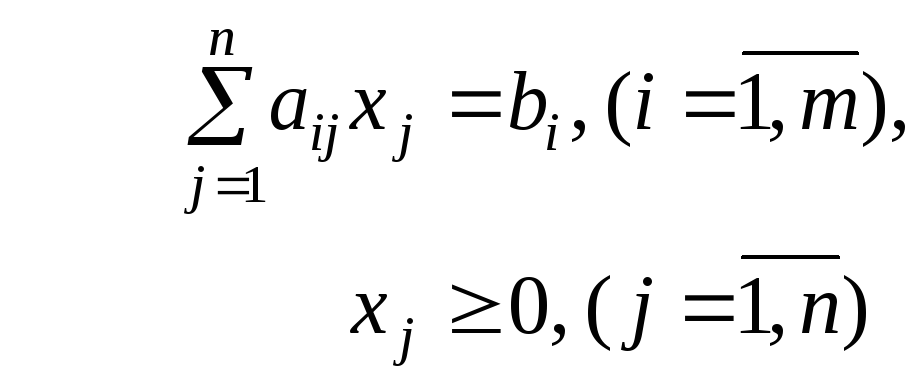
можно преобразовать любую задачу. Равенство эквивалентно двум неравенствам с противоположными знаками:

и .

Умножая последнее неравенство на –1, получим задачу в симметричной форме:

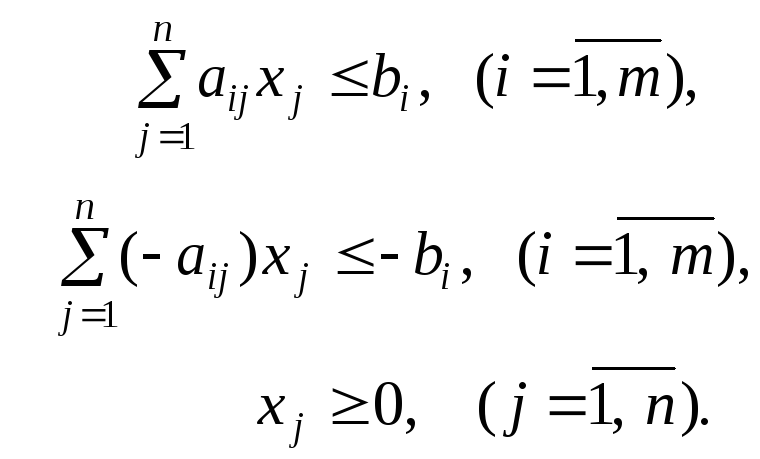
Если обозначить двойственные переменные для каждой из двух записанных групп ограничений как и 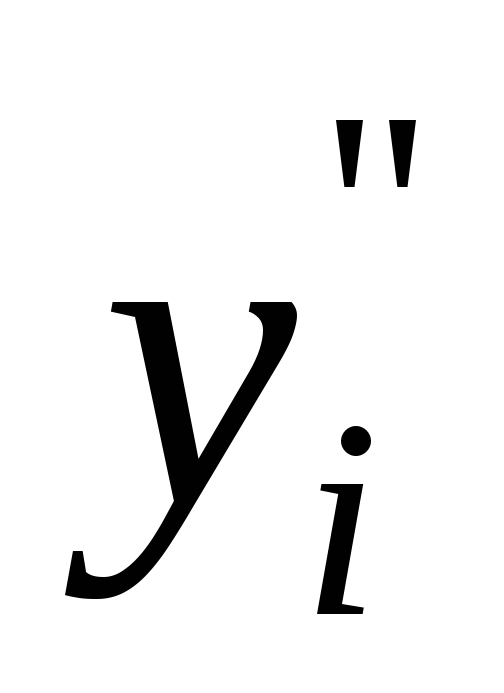, то двойственной задачей будет:

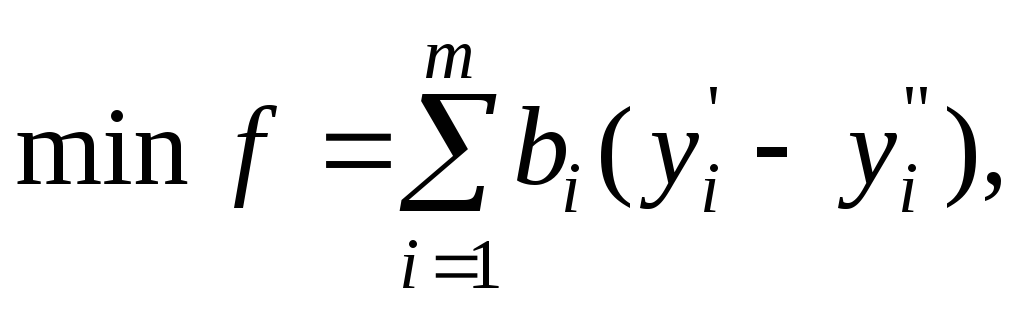
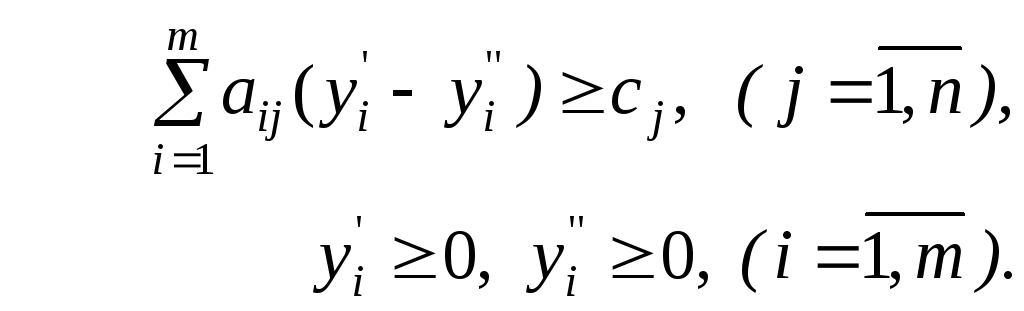
Разность двух неотрицательных переменных эквивалентна одной переменной произвольного знака, т. е. 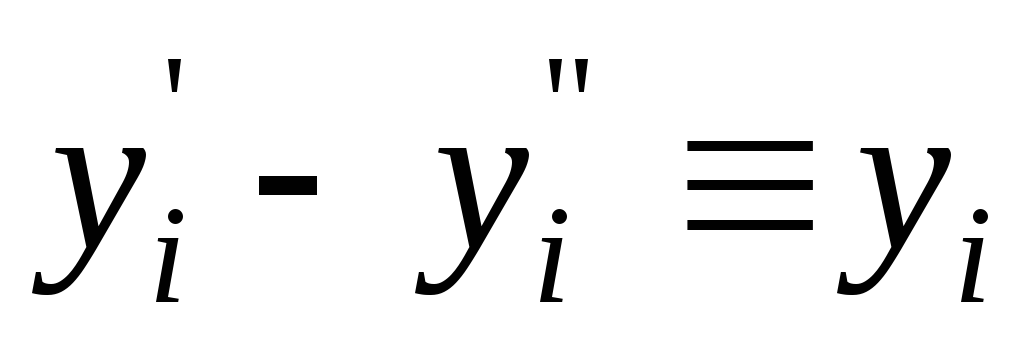. Следовательно, переменную произвольного знака можно рассматривать как соответствующую i-му ограничению-равенству прямой задачи в канонической форме. Двойственная задача будет иметь вид:

Следовательно, если в прямой задаче есть ограничение в виде равенства, то соответствующая переменная двойственной задачи обязательно будет произвольного знака. Подобным образом можно обосновать правила построения двойственных задач для случая, когда прямая задача представлена в общей форме (табл. 3.2).

Таблица 3.2

Задача максимизации		Задача минимизации
Ограничения		Переменные
		Любого знака
Переменные		Ограничения
Любого знака

3.3. Соотношения между решениями прямой и двойственной задач

Тесная взаимосвязь прямой и двойственной задач позволяет сформулировать ряд общих закономерностей.

Основное неравенство теории двойственности.

Для любых допустимых планов и прямой и двойственной задач справедливо неравенство , т. е.

.

Пусть задачи уже представлены в симметричной форме. Тогда

и

последовательно выполняя подстановки, получаем

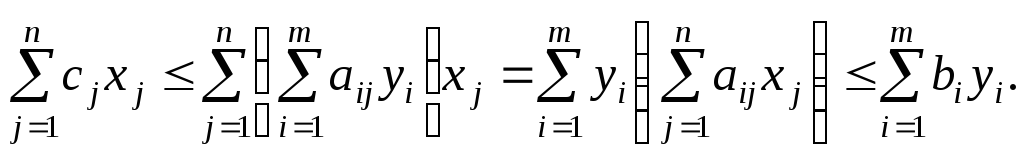
Это неравенство позволяет привести интересную экономическую интерпретацию: общая созданная стоимость не превосходит суммарной оценки ресурсов.

Критерий оптимальности Канторовича.

Если для некоторых допустимых планов и у^* пары двойственных задач выполняется равенство , то и у^* являются оптимальными планами соответствующих задач.

Иначе говоря, если вновь созданная стоимость равна суммарной оценке ресурсов, то решения каждой из задач оптимальны.

Доказательство основывается на предыдущем неравенстве, согласно которому всегда . Для допустимого плана двойственной задачи оно также справедливо . Но по условию , следовательно, и доказано, что план является оптимальным для прямой задачи. Оптимальность вектора для двойственной задачи доказывается аналогично.

Малая теорема двойственности.

Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.

Если оптимальные планы для этих задач существуют, то они же являются и допустимыми, следовательно, необходимость доказана. Для доказательства достаточности предположим, что допустимые планы и существуют. Но тогда , значит функционал прямой задачи для любого допустимого плана не может превысить указанное значение. Следовательно, существует оптимальный план , для которого . Существование оптимального плана доказывается аналогично.