2. Методологія оцінювання параметрів (коефіцієнтів) економетричних моделей

2.1 Вимоги до вихідних даних при побудові багатофакторної економетричних моделі

Основною вимогою, якій повинен задовольняти досліджуваний процес, це адитивність його детермінованої складової з випадковою складовою , тобто

(2.1)

Наступною за важливістю вимогою є лінійність f(x₁, x₂, ..., x_n) від невідомих коефіцієнтів моделі, тобто

, (2.2)

де: а_i - невідомі коефіцієнти.

Фактори х_i можуть бути як безпосередніми характеристиками процесу, так і деякими функціями від них (наприклад, , , і подібне до того). Будемо вважати, що ця вимога виконується і для моделей типу (1.9), в які невідомі коефіцієнти входять нелінійно, але котрі шляхом деяких перетворень, наприклад, логарифмування, зводяться до моделей лінійних відносно деяких функцій від цих коефіцієнтів. Так (1.9), шляхом логарифмування зводиться до

(2.3)

З (2.3) випливає, що невідомі коефіцієнти ln a, b, c та r входять лінійно до рівняння, при цьому ; ; .

Результати дослідження процесу можна подати в матричній формі:

, (2.4)

де - вектор з m виміряних значень залежної (ендогенної) перемінної;

- матриця розмірності m×(n+1) (n- число незалежних (ендогенних) перемінних, причому для i ≠ 0 стовпець складається з m вимірних значень , якщо і=0, то стовпець містить m одиниць.

- вектор-стовпець оцінюваних параметрів (коефіцієнтів) моделі розмірності m + 1,

- вектор похибок розмірності m, тобто

.

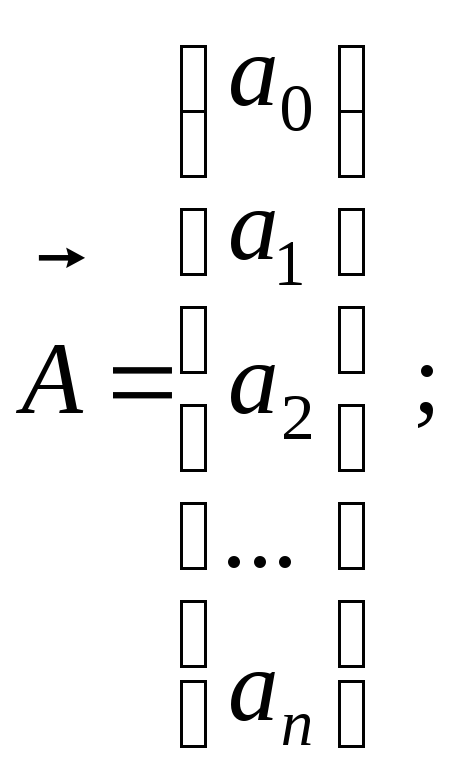
2.2 Метод найменших квадратів (мнк)

Метод найменших квадратів полягає в тому, що оцінки невідомих параметрів , у моделі (2.2) визначаються за умови min , тобто сума квадратів відхилень фактичних значень змінної у від розрахункових значень показника, отриманих за моделлю з параметрами , повинна бути мінімальною.

Для пошуку невідомих параметрів моделі методами найменших квадратів повинні виконуватись такі вимоги [1]:

1. , де М – математичне сподівання;

б) , тобто значення похибок незалежні й мають сталу дисперсію;

в) ; тобто незалежні змінні не пов’язані з похибками.

г) |x^Tx| 0, отже, незалежні змінні утворюють лінійно незалежну систему векторів або, іншими словами, незалежні змінні не повинні бути мультиколінеарними.

Для пошуку шукаємо частинні похідні за параметрами , і=1, 2, . . . , n і отримуємо систему нормальних рівнянь [2]

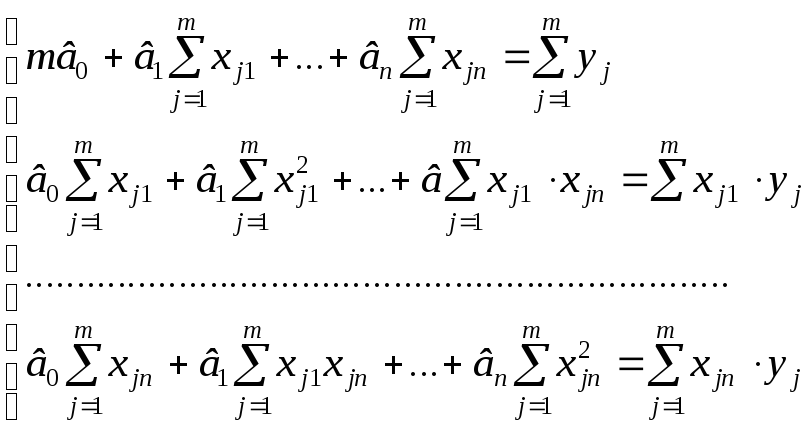(2.5)

Це система з (n+1) рівнянь з n+1 - невідомим. При виконанні умови (г) матриця системи х^Тх невироджена (|x^Tx| 0), і тому для неї існує єдине вирішення, набір параметрів . Пошук оцінок невідомих параметрів моделі можна виконати також і у матричній формі. Якщо = x + , тоді = - X і

= (2.6)

Для визначення , що мінімізує суму квадратів відхилень , продиференціюємо (2.6) по

(2.7 )

Прирівнявши (2.7) до нуля, одержимо нормальну систему рівнянь (2.5) у матричній формі, яка матиме вигляд

(2.8 )

При виконанні умови (г) (|x^Tx| 0) одержимо розв'язання цієї системи, оцінювання параметрів ,

= (2.9)

Матрицю |x^Tx| називають матрицею моментів; числа, що розташовані на її головній діагоналі, , характеризують величину дисперсій незалежних перемінних х_i, інші елементи цієї матриці відповідають взаємним коваріаціям факторів х_i, х_k. Таким чином, структура матриці моментів |x^Tx| відображає зв'язок між незалежними перемінними. Чим більші коваріації між незалежними параметрами у порівняно з діагональними елементами |x^Tx|, тим гірші, отже, оцінювання .

Знайдемо математичне сподівання і дисперсію оцінок , отриманих М.Н.К.

(2.10 )

Тоді М( ) =

Але внаслідок умови (а) М() = 0. Тоді М() = ,

отже, оцінка параметрів є незміщеною.

Для пошуку дисперсій оцінок розглянемо матрицю . Це матриця, на головній діагоналі якої розташовані дисперсії оцінок : , а інші елементи дорівнюють коваріаціям оцінок і : .

Тоді, з урахуванням (2.10), матимемо:

.

Враховуючи, що матриця симетрична, отже а також, за умовою (б), , отримаємо:

. (2.11 )

Тоді можна довести [3], що дисперсії для оцінок _i, отриманих за МНК, є мінімальними у класі всіх лінійних незміщених оцінок. Отже, отримані оцінки _i є ефективними.

Можна показати [3], що ці оцінки є обгрунтованими. Можна показати також [3], що ці оцінки є обгрунтованими. Для ілюстрації МНК розглянемо випадок одного фактора х та показника y, тобто оцінимо коефіцієнти у моделі y = a₀ + a₁x₁ (n=1)

Матриця Х у цьому випадку має вигляд х =

Тоді з (1.8)

звідси

;

де

,

Пошук оцінок параметрів лінійної спрощується, якщо використовується стандартизовану форму рівняння регресії (2.2). Для цього використовується нормалізація ендогенних та екзогенних змінних за формулами.

(2.12 )

де

. (2.13 *)

Рівняння регресії (2.2) після використання цих підстановок набуває стандартизованої форми з відсутнім вільним членом, тобто

(2.14 )

Коефіцієнти при нормалізованих факторах t_k називаються -коефіцієнтами. Вони характеризують силу впливу кожного фактора на показник у. Підставляючи з (2.12) до (2.14) і порівнюючи з (2.12), маємо ^, (2.15 )

При використанні стандартизованої форми пошук оцінок параметрів моделі спрощується. Дійсно, в цьому випадку матриця системи нормалізованих факторів Т має на один стовпець менше, dim Т = (m; n), а матриця моментів Т^ТТ обертається на кореляційну:

T^TT = R = (2.16)

де - вибірковий коефіцієнт кореляції між факторами х₁ і х_k. Тоді за аналогією (2.9) можна одержати, що

(2.17)

З огляду на те, що (2.18)

де - вектор, складений із вибіркових коефіцієнтів кореляції між показником в і факторами х_k,

, одержимо (2.19)

Таким чином, для визначення оцінок параметрів у рівнянні (2.2) необхідно:

1) знайти за вищенаведеними формулами вибіркові коефіцієнти кореляції між факторами і скласти з них кореляційну матрицю R;

2) якщо , то обчислити обернену матрицю R^-1;

3) обчислити вибіркові коефіцієнти кореляції між показником у і факторами ;

4) відшукати за формулами (2.19);

5) відшукати за формулою (2.15) знайти , , k = 1, 2, ..., n.