2.Структурні схема оптимального когерентного демодулятора сигналов с ам, чм и офм.

При заваді з рівномірним спектром в сигналах , , заданих на кінечному інтервалі , умова оптимального прийому за В.А. Котельниковим може бути представлена у вигляді:

Цей вираз визначає умови правильного прийому сигналу .

У випадку, коли апріорні ймовірності сигналів однакові критерій Котельникова приймає більш простий вигляд:

(4.3)

Звідси випливає, що при рівноймовірних сигналах оптимальний приймач відтворює повідомлення, яке відповідає тому переданому сигналу, який має найменше середньоквадратичне відхилення від прийнятого сигналу.

Записану вище нерівність (4.3) можна записати в іншому вигляді:

Для сигналів, енергії яких однакові, ця нерівність для всіх приймає більш просту форму:

(4.4)

В цьому випадку умова оптимального прийому (4.4) можна сформувати наступним чином. Якщо всі можливі сигнали рівно ймовірні і мають однакову енергію, оптимальний приймач відтворить повідомлення, відповідне тому переданому сигналу, взаємна кореляція якого з прийнятим сигналом максимальна.

Для двійкової системи отриманим результатам можна дати наглядне геометричне трактування (рис. 4.6).

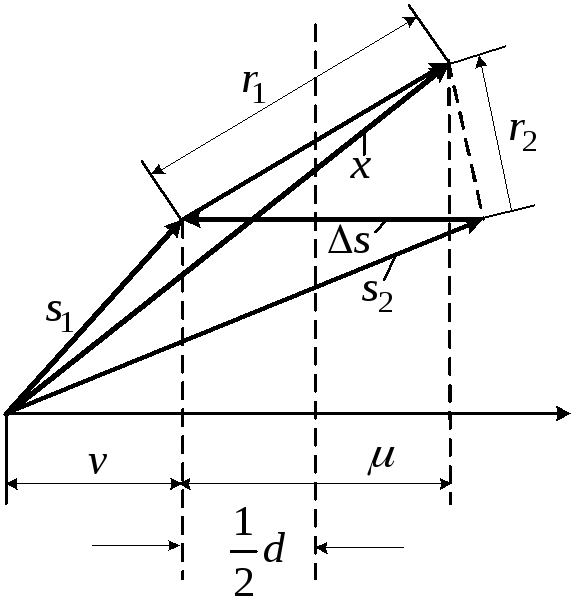
Рис4.6.

Нехай передаються два рівноймовірних повідомлення і за допомогою сигналів і . Простір можливих значень сигналу можна розбити на дві області, так, щоб при попаданні кінця вектора в першу область відтворювався сигнал (область ), а при попаданні в другу область – відтворився сигнал (область сигналу ). Ймовірність помилки, очевидно, залежить від конфігурації областей сигналу. В оптимальному приймачі Котельникова простір сигналів розбивається на область сигналу і так, щоб повна ймовірність помилки була мінімальною.

У випадку рівноймовірності сигналів і завади з рівномірним розподілом оптимальне розбиття простору буде таким, при якому люба точка відноситься до області того сигналу , кінець вектора якого найближчий до точки . В двовимірній моделі для двійкової системи границя областей сигналів і є геометричне місце точок, рівновіддалених від і , тобто гіперплощина, перпендикулярна до вектора різниця і яка поділяє його навпіл (рис. 4.6).

Якщо, наприклад, передавався сигнал , то помилка відбудеться в тому випадку, коли виконується нерівність:

чи

,

де , і - проекція на вектор, колінеарний до , тобто:

.

Очевидно, що можна записати:

або в евклідовій метриці:

Ця умова повністю співпадає з записаною раніше умовою (3) для рівноймовірних сигналів.

0. Структурна схема оптимального приймача в.А. Котельникова для рівноймовірних сигналів

Структурна схема оптимального приймача зображена АН рис. 4. 7. Умова прийому для двох сигналів визначиться виразом:

(4.5)

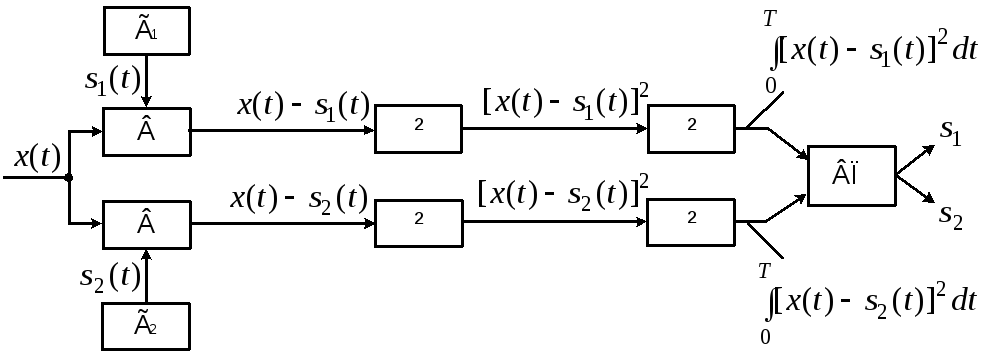
Рис.4.7.

Генератори опорних сигналів Г₁ і Г₂ – формують точні копії переданих сигналів і . В – вираховуючий пристрій, КВ – квадратуючий пристрій. І – інтегратор, ВП – вирішуючий пристрій.

Нерівність (4.5) можна записати в іншому вигляді:

або

Ця нерівність еквівалентна нерівності (4.5), але веде до іншої схемної реалізації приймача (рис. 4.8).

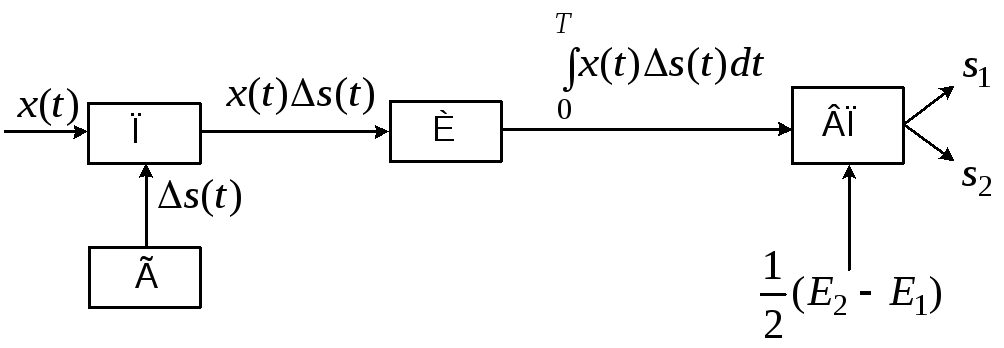
Рис.4.8.

В схемній реалізації після операції перемноження (П), інтегрування (І) проводиться порівняння отриманого результату з постійним порогом, рівним різниці енергій та сигналів . Ця схема простіша від запропонованої раніше, однак вона володіє тим недоліком, що при зміні рівня сигналу поріг потрібно автоматично регулювати. Цей недолік усувається для сигналів рівних енергій ; тоді поріг дорівнює нулю, і вирішуючи схема визначає тільки знак сигналу на виході.