Определение случайной ошибки

Если исходить из предположения, что все систематические ошибки учтены, то в качестве результата измерения можно рассматривать наиболее вероятное значение соответствующей случайной величины. Чтобы найти это наиболее вероятное значение или хотя бы оценить его точность нужно знать распределение случайной величины.

Анализ различных случайных величин, как изучаемых теоретически, так и вычисляемых на основании опытов, показывает существование одного наиболее часто встречающегося распределения, называемого нормальным или распределением Гаусса.

Распределение Гаусса получено на основе следующих двух допущений:

1) окончательная ошибка любого измерения представляет собой результат большого числа очень малых величин, распределенных случайным образом;

2) положительные и отрицательные отклонения относительно истинного значения равновероятны; и имеет вид рис. 1 (где f(x) плотность вероятности, 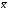- наиболее вероятное значение).

рис. 1

Кривая, изображенная на рис.1. непрерывна, т.е. описывает совокупность, содержащую бесконечное множество измерений, Это так называемая генеральная совокупность, из которой для исследования берутся некоторые конечные выборки.

Погрешность прямых, многократных, равноточных измерений одной и той же физической величины

Рассмотрим выборку из n отсчетов, содержащую значения x₁, x₂, x₃, …, x_n полученные при повторных измерениях одной и той же величины. Допустим, что эти отсчеты составляют некоторую часть бесконечной нормально распределенной совокупности с неизвестным истинным значением.

Из свойства нормального распределения случайных величин следует, что наиболее вероятное значение равно среднему арифметическому значению полученных n отсчетов

(1)

Таким образом, в качестве результата измерений величины x нужно брать не числа x₁, x₂, x₃, …, x_n, а число .

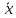Погрешность этого результата будет значительно меньше, но не следует думать, что будет в точности равно истинному значению, так как 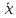играет роль центра рассеяния.

Из эксперимента мы можем найти только отклонения отсчетов х_i, от среднего 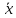. Эти отклонения мы обозначим через Δx_i:

(2)

Выборочной дисперсией 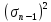(или s²) измерения называют величину

(3)

Квадратный корень из выборочной дисперсии, т.е. величину 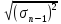, называют среднеквадратичной погрешностью одного измерения:

Среднеквадратичная погрешность характеризует степень разброса единичных измерений относительно x: в интервал 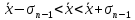попадает примерно половина всех отсчетов х_i.

Среднеквадратичное отклонение среднего значения 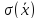можно вычислить по формуле

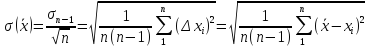(5)

Так как обычно число измерений n существенно меньше, чем требуется, то истинное значение x лежит в доверительном интервале 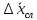, определяемом условием (6), с определенной доверительной вероятностью α.

(6)

где – коэффициент Стьюдента; n - объем выборки.

Значение коэффициента Стьюдента берется из таблицы 1. При выполнении лабораторных работ доверительная вероятность обычно выбирается равной 0,95 (95%)

Условие (6) представляет собой абсолютную случайную ошибку измерений.

Тогда результат измерения величины x будет находиться в интервале значений

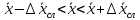(7)

Относительная погрешность измерений равна

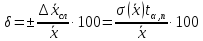(8)

Таблица 1. Коэффициенты Стьюдента (часть таблицы, полный вариант см. приложение)

	n	1		2		3		4		5		6		7		8		9		10			20
α
0.9			6.31		2.92		2.35		2.13		2.02		1.94		1.89		1.86		1.83		1.81	1.72
0.95			12.7		4.3		3.18		2.78		2.57		2.45		2.36		2.31		2.26		2.23	2.09
0.99			63.66		9.92		5.84		4.6		4.03		3.71		3.5		3.36		3.25		3.17	2.85
0.999			636.6		31.6		12.94		8.61		6.86		5.96		5.41		5.04		4.78		4.59	3.85