механика

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Томский государственный архитектурно-строительный университет»

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ

Методические указания к самостоятельному изучению темы

Составители В.Г. Симоненко, О.Н. Лысак

Томск 2012

Теоретическая механика. Связи и реакции связей: методические указания к самостоятельному изучению темы / Сост. В.Г. Симоненко, О.Н. Лысак. – Томск: Изд-во Том. гос. архит.-

строит. ун-та, 2012. – 33 с.

Рецензент ст. препод. М.В. Геттингер Редактор Е.Ю. Глотова

Методические указания предназначены для самостоятельного изучения темы «Связи и реакции связей» и соответствуют государственному образовательному стандарту подготовки бакалавров и специалистов по дисциплине «Теоретическая механика» всех направлений всех форм обучения.

Печатаются по решению методического семинара кафедры теоретической механики, протокол № 3 от 3 октября 2011 г.

Утверждены и введены в действие проректором по учебной работе В.В. Дзюбо

с 01.11.2012 по 01.11.2017

Оригинал-макет подготовлен авторами

Подписано в печать 30.11.12. Формат 60×84. Бумага офсет. Гарнитура Таймс.

Уч.-изд. л. 1,7. Тираж 140 экз. Заказ № 555.

Изд-во ТГАСУ, 634003, г. Томск, пл. Соляная, 2. Отпечатано с оригинал-макета в ООП ТГАСУ.

634003, г. Томск, ул. Партизанская, 15.

2

3

Образование – это то, что остаётся, когда мы уже забыли всё, чему нас учили.

Д. Галифакс (XVIII в.)

ВВЕДЕНИЕ

Большинство законов классической механики выведены для свободных материальных объектов, в число которых входят материальные точки, механические системы и твёрдые тела. Как правило, все эти объекты на практике являются несвободными. В связи с этим возникает проблема выявления связей, ограничивающих движение объектов и правильного освобождения от них.

Представленные методические указания дают возможность дополнительно проработать данную тему и получить знания, позволяющие приобрести необходимые умения и навыки для успешного решения поставленных задач.

В результате изучения темы «Связи и реакции связей» сту-

дент должен обладать стремлением к саморазвитию, повышением своей квалификации и мастерства (ОК-6), для этого необходимо:

1)творчески подойти к изучению представленного теоретического материала, дополняя в случае необходимости проработку рекомендуемой литературы для дальнейшего успешного решения задач как теоретической механики, так и задач сопротивления материалов. Для этого требуется качественно разобрать понятие связей, научиться правильно их классифицировать;

2)уметь правильно освобождаться от выявленных связей, заменяя их реакциями, приложенными к данному телу (механизму);

3)владеть полученными знаниями при решении практических задач, получая при этом необходимые навыки.

4

1. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ

Свободным материальным объектом называется такой объект, который не скреплён с другими материальными объектами и которому из данного положения можно сообщить любое перемещение в пространстве под действием приложенной к нему системы сил или, другими словами, объект, не имеющий никаких закреплений, препятствующих его движению.

Под материальными объектами будем понимать материальную точку, механическую систему и её частный случай – абсолютно твёрдое тело (твёрдое тело).

При решении большинства задач механики приходится иметь дело с теламинесвободными, т. е. стакими, которые соприкасаются или скреплены с другими телами, благодаря чему становятся невозможными те или иные перемещения данного тела. Если тело несвободно,то говорят, чтонанего наложены связи.

Любое тело, ограничивающее свободу перемещения данного объекта, называется связью, наложенной на этот объект. Иначе это понятие можно выразить так: связью называется любая конструкция, уменьшающая количество степеней свободы данного материального объекта.

Количеством степеней свободы материального объекта называется число независимых параметров, с помощью которых можно определить (задать) его положение на плоскости или в пространстве. Каждая связь имеет свою кинематическую характеристику, которая показывает, каким движениям материального объекта она препятствует и сколько степеней свободы она уничтожает (отнимает).

Так, пространственное свободное твёрдое тело, изображённое на рис. 1, а, может совершать независимые поступательные движения вдоль трёх осей декартовой системы координат и три вращательные движения вокруг тех же осей. Следовательно,

5

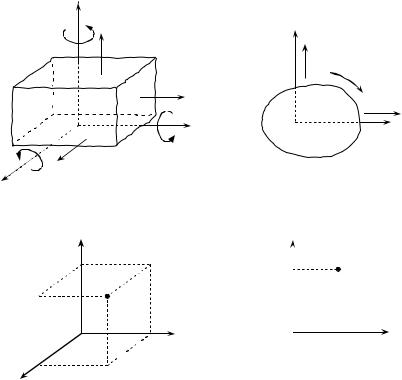
пространственное свободное твёрдое тело имеет шесть степеней свободы. Плоское твёрдое тело, показанное на рис. 1, б, может совершать на плоскости два независимых поступательных перемещения (вдоль осей x и y) и одно вращательное движение вокруг какого-либо центра вращения (точки), называемого полюсом. Отсюда, плоское свободное твёрдое тело на плоскости имеет три степени свободы.

y

6

Положение любой свободной точки М в пространстве (рис. 1, в) может быть определено тремя координатами xM , yM , zM , т. е. она имеет три степени свободы, а на плоскости

(рис. 1, г) – двумя координатами xM , yM и соответственно имеет две степени свободы.

Для дальнейшего понимания излагаемого материала вспомним аксиому сил действия и противодействия. Рассмотрим важный случай взаимодействия двух материальных объектов (точек, тел) А и В. Пусть, например, точка А действует на точку В с силой FA . Назовём эту силу силой действия. Точка В будет

обязательно противодействовать на точку А с силой FB . Эту силу назовём силой противодействия.

FB FA

АВ

Аксиома утверждает: всякой силе действия есть равная по модулю, но противоположно направленная вдоль прямой, соединяющей эти точки, сила противодействия.

Современная трактовка аксиомы такова:

силы, с которыми действуют друг на друга две точки (тела), всегда равны по модулю и противоположно направлены вдоль прямой, соединяющей эти точки, т. е.

FВ FА .

Согласно этой аксиоме между данным телом и связью (опорой) существует механическое взаимодействие. Воздействие тела на связь называется силой действия, которая всегда приложена к связи. Воздействие же связи на тело – силой противодействия.

Сила противодействия связи, приложенная к рассматри-

ваемому телу, называется реакцией связи.

7

Силы действия и противодействия не образуют уравновешенную систему сил, так как они приложены к разным телам: силы действия приложены к связи, силы противодействия – к данному телу (объекту).

Основные законы классической механики записаны для свободных материальных объектов. Условия равновесия для различных конструкций также получены исходя из того, что они должны быть свободными, т. е. освобождёнными от связей.

В связи с этим возникла необходимость сформулировать принцип (аксиому) освобождения от связей:

любое несвободное тело можно условно представить свободным, если мысленно освободить его от связей, заменив действие этих связей соответствующими реакциями, приложенными к рассматриваемому телу.

Пользуясь этим принципом, к несвободному телу можно применять условия равновесия, выведенные в статике для свободного тела. Нужно только в число сил, действующих на тело, обязательно включать и силы реакций связей.

Большинство задач статики как раз и заключается в определении сил реакций связей. При знании их будут известны и силы давления на связи, т. е. будут известны данные, необходимые для расчёта на прочность самихконструкций.

В механических системах, образованных путём сочленения нескольких твёрдых тел, наряду с внешними связями (опорами) имеются внутренние связи междувзаимодействующими телами.

Внутренней связью называется такая связь, которая не препятствует перемещению всей системы в целом, а налагает ограничения только наотносительное расположение точек (тел) системы.

Опорными называются связи, осуществляющие прикрепление конструкции к некоторомуоснованию (например, к земле).

Так как прикрепление может быть осуществлено различными способами, необходимо научиться правильно классифи-

8

цировать наложенные на материальный объект связи и правильно от них освобождаться.

Значение реакции связи зависит от других действующих сил, и наперёд неизвестно (если никакие другие силы на тело не действуют, реакции равны нулю); для её определения надо решить соответствующую задачу механики. В общем случае реакция связи направлена в сторону, противоположную той, куда связь не даёт перемещаться телу. Когда связь может препятствовать перемещениям тела по нескольким направлениям, направление реакции такой связи тоже наперёд неизвестно и должно определяться в результате решения задачи.

Правильное определение направлений реакций связей при решении задач механики играет очень важную роль.

Рассмотрим, как классифицируются различные типы связей и как правильно освободиться от них.

1.1.СВЯЗИ, ИСПОЛЬЗУЕМЫЕ

ВПЛОСКИХ КОНСТРУКЦИЯХ ЗАДАЧ СТАТИКИ

1.1.1.Гладкая опорная поверхность, опорное ребро

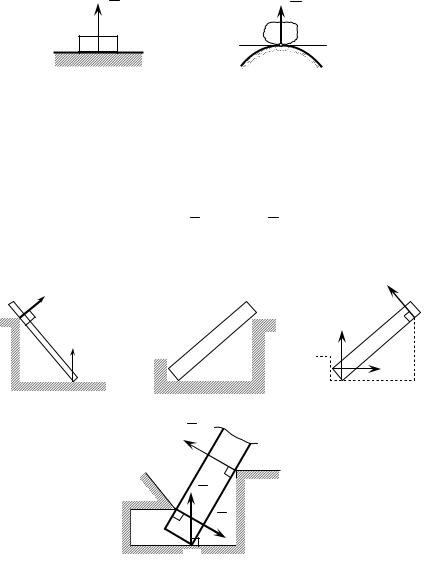
Гладкой называется поверхность, трением тела о которую можно пренебречь (связи без трения относятся к так называемым идеальным связям, рассмотрением таких связей мы пока и ограничимся).

Так как гладкая опорная поверхность не препятствует

скольжению по ней поверхности тела, то реакция N гладкой по-

верхности (рис. 2) направлена всегда по нормали к поверхности тела и поверхности связи в их точке касания. Нормалью к по-

верхности называется перпендикуляр к касательной плоскости, проведённый через точку касания.

9

N N

Рис. 2

Если одна из соприкасающихся поверхностей имеет заострение (уступ, угол) (рис. 3), то реакция должна быть направлена по нормали к другой гладкой поверхности (такой вид связи иногда называют опорное ребро). Например, к гладкому брусу АВ (рис. 3, а), опирающемуся в точке А на пол и в точке В на ребро

стены, приложены реакции RA пола и RB ребра, направленные так, как изображено на рисунке.

г RC

С

Рис. 3

10