1.4. Обернена задача кiнематики

Обернена задача кiнематики полягає в знаходженнi рiвняння руху за вiдомими характеристиками руху.

Розглянемо, як за вiдомими i можна знайти рiвняння руху в траєкторному виглядi . Запишемо з виразу (1.12) елементарний шлях, пройдений за час :

(1.32)

Щоб знайти весь шлях, пройдений за певний промiжок часу , слід проiнтегрувати цей вираз:

(1.33)

Графiчно цей iнтеграл зображений на рис. 1.10, з якого видно, що шлях чисельно дорiвнює площi фiгури (криволiнiйної трапеції), що обмежена кривою .

Аналогiчно за вiдомим прискоренням можна знайти швидкiсть у довiльний момент часу :

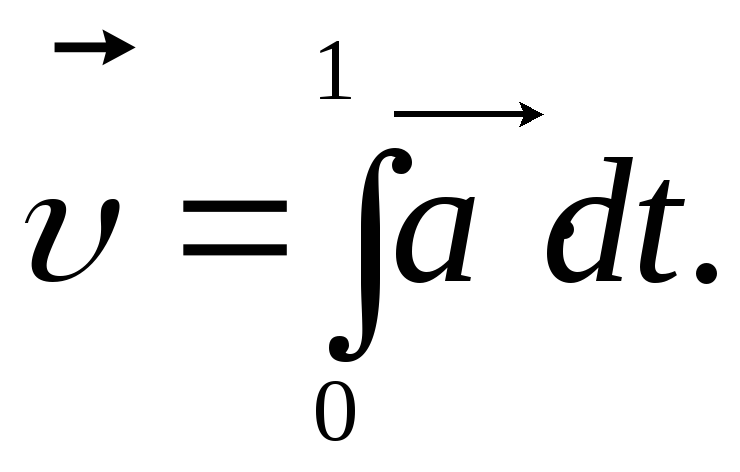(1.34)

Якщо в початковий момент часу , тiло мало початкову швидкiсть , то

(1.35)

Застосуємо наведенi вирази для рiвнозмiнного прямолiнiйного руху при . Тодi рiвняння (1.35) перепишеться:

(1.36)

З виразу (1.33) можна одержати:

Остаточно:

(1.37)

Знайшовши з виразу (1.36) i пiдставивши його у вираз (1.37), можна одержати рiвняння, яке часто зручно використовувати в задачах:

(1.38)

1.5. Рух матерiальної точки по колу

Пiд час розглядання руху матерiальної точки по колу крім характеристик , якi в даному разi називаються лiнiйними, зручно користуватися так званими кутовими характеристиками руху: кутом повороту, кутовою швидкiстю, кутовим прискоренням.

1.5.1 . Кут повороту

Положення матерiальної точки пiд час руху по колу можна визначити кутом повороту . Як видно з рис. 1.11,а, кут повороту з центральним кутом, який вiдповiдає дузi , описанiй матерiальною точкою за час . Вимiрюється кут повороту в радiанах (рад) i є скалярною величиною. Один оберт точки по колу дорiвнює 2, а при N обертах:

(1.39)

Із геометрiї вiдомий зв’язок мiж довжиною дуги та кутом повороту:

(1.40)

де R— радiус кола. Для малих промiжкiв часу цей вираз матиме вигляд:

(1.41)

де - елементарний кут повороту. Для того, щоб показати i напрямок руху точки по колу, домовились елементарний кут повороту показувати як вектор , що вiдкладається вздовж осi обертання. Напрямок вектора визначається за правилом правого гвинта: вектор елементарного кута повороту збiгається за напрямком з поступальним рухом гвинта, ручка якого обертається в напрямку руху точки по колу (рис. 1.11,а). Такi „штучні” вектори називаються псевдовекторами.

1.5.2. Кутова швидкiсть

Аналогiчно до означень, наведених в п. 1.3.2, розрiзняють середню і миттєву кутові швидкостi. Середня кутова швидкiсть () визначається вiдношенням кута повороту до вiдповiдного промiжку часу :

(1.42)

Для миттєвої кутової швидкостi (або просто кутової швидкості ) можна записати:

(1.43)

тобто чисельно вона дорiвнює похiднiй кута повороту за часом. Вимiрюється кутова швидкiсть у радiанах за секунду (рад/с). Вона теж є псевдовектором, що напрямлений вздовж осi обертання, вiдповiдно до правила гвинта (рис. 1.11). Тому можна записати у векторному виглядi:

(1.44)

Якщо з часом кутова швидкiсть не змiнюється, тобто , рух по колу називається рiвномiрним, для нього

(1. 45)

У цьому разі називають циклічною частотою обертання. Час, за який матерiальна точка проходить один оберт по колу, називається перiодом обертання Т, який вимiрюється в секундах. Вираз (1.45) дає:

(1.46)

звідки

Величина, обернена до перiоду, називається частотою обертання :

(1.47)

Вона показує, скiльки обертiв по колу робить точка за одиницю часу i вимiрюється в секунду мінус першій ступені ( с^-1 ) або в герцах (Гц). Зв’язок мiж частотою i кутовою частотою має такий вигляд:

(1.48)