1.3. Кiнематичнi характеристики поступального руху матерiальної точки

До кiнематичних характеристик поступального руху вiдносяться: перемiщення, швидкiсть та прискорення.

1.3.1. Перемiщення

Нехай у момент часу t матерiальна точка пребувала в положеннi 1, а за деякий промiжок часу ∆t — в положеннi 2 (рис. 1.6,а).

Проведемо радiус-вектори і в точки 1 i 2. Тодi вектор перемiщення визначиться як

(1.8)

тобто вектор перемiщення являє собою змiну (прирiст) радіуса-вектора за часом. З урахуванням (1.3) вектор ∆r можна записати через прирiст координат матерiальної точки (∆х, ∆у, ∆z ) за час ∆t:

(1.9)

а його модуль як

(1.10)

Як видно з рис. (1.6,б) вектор перемiщення збiгається з хордою, що стягує вiдповiдну дiлянку траєкторії. Тому завжди, крiм прямолiнiйного руху, модуль вектора перемiщення менший, нiж шлях, пройдений за той же промiжок часу:

(1.11)

Тепер будемо зменшувати промiжок часу ∆t до достатньо малого значення, яке назвемо елементарним i позначимо dt. При цьому вiдбудеться також мале перемiщення, яке називатиметься відповiдно елементарним перемiщенням d i матерiальна точка пройде досить малий, тобто елементарний шлях dS. Ясно, що iз зменшенням ∆t значення ∆r буде все бiльше наближатися до ∆S. Тобто при () можна вважати, що

dr = dS (1.12)

За напрямком d буде спрямовано по дотичній до траєкторiї в бiк руху матерiальної точки. Позначимо орт дотичної , тодi у векторному виглядi можна записати (при ):

1.3.2. Швидкість

Розрiзняють швидкiсть середню i миттєву. Середньою швидкiстю перемiщення () за промiжок часу ∆t називається векторна величина, що дорiвнює вiдношенню вектора перемiщення до цього промiжку часу:

(1.13)

Вектор спрямований так, як i вектор (рис. 1 .7,а).

Будемо нескiнченно зменшувати промiжок часу, направляючи його до нуля (). Показано, що при цьому, починаючи з деяких значень ∆t, вiдношення перестає змiнюватися. Тобто iснує певна границя, до якої прямує вiдношення при .

Ця границя i визначає швидкiсть руху в даному мiсцi траєкторiї в даний момент часу, тобто миттєву швидкiсть (при цьому точки 1 i 2 на рис. 1.7,а будуть нескiнченно наближатися одна до одної).

(1.14)

Враховуючи (1.12) одержимо:

(1.15)

Швидкість, це фізична величина , що показує, як змінюється переміщення матеріальної точки за одиницю часу.

1.3.3. Прискорення

Прискоренням називається фiзична величина, що характеризує змiну швидкостi з часом. Розрiзняють прискорення середнє i миттєве.

Середнє прискорення ()— це векторна величина, що визначається вiдношенням змiни швидкостi до промiжку часу , за який ця змiна вiдбулася:

(1.16)

Напрямок вектора збігається з напрямком .

Миттєве прискорення (або просто прискорення) , тобто прискорення в певний момент часу це границя, до якої прямує середнє прискорення при

(1.17)

Використовуючи рівність (1.16) маємо,

(1.18)

Прискорення є векторна величина, що дорівнює похiднiй вектора швидкості за часом. З урахуванням формули (1.16) прискорення можна записати як другу похiдну радіус-вектора за часом:

(1.19)

Як буде показано далi, в загалом вектор спрямований пiд кутом до вектора в бiк угнутостi траєкторiї. На рис. 1.8. вектор вiдповідає прискореному руху, вектор —сповiльненому руху. Оскiльки змiна швидкостi вiдбувається i за модулем i за на напрямком, розрiзняють двi складовi прискорення:

- прискорення (дотичне), яке характеризує змiну швидкості за модулем i спрямоване по дотичнiй до траєкторії;

- нормальне прискорення (доцентрове), яке характеризує змiну швидкості за напрямком i спрямоване по нормалi до траєкторії.

Повне прискорення дорівнює їх векторнiй сумi

(1.20)

Для знаходження цих складових прискорення, пiдставимо вираз для швидкостi в означення (1.18) i зробимо вiдповiдне диференцiювання:

Враховуючи, що , а можна подати у виглядi:

Матимемо вираз:

(1.21)

Можна показати, що

, (1.22)

де - орт нормалі, R – радіус кривизни траєкторії в даній точці.

Остаточно вираз (1.21) набуде вигляду:

(1.23)

Порiвнюючи цей вираз з рiвнянням (1.20) бачимо, що перший член виразу визначає тангенцiальне прискорення

(1.24)

що спрямоване по дотичнiй до траєкторiї в данiй точцi i за модулем дорівнює

. (1.25)

Другий член визначає нормальне прискорення

, (1.26)

що спрямоване по нормалi до траєкторії в данiй точцi (тобто до центру кривизни траєкторiї) i за модулем дорівнює

(1.27)

Як видно з рис.1.9, модуль повного прискорення

(1.28)

Аналогiчно до того, як записувався вектор швидкостi, вектор прискорення теж можна подати через проекцiї на координатнi осi:

(1.29)

(1.30)

Цi проекцiї знаходяться як похiднi за часом:

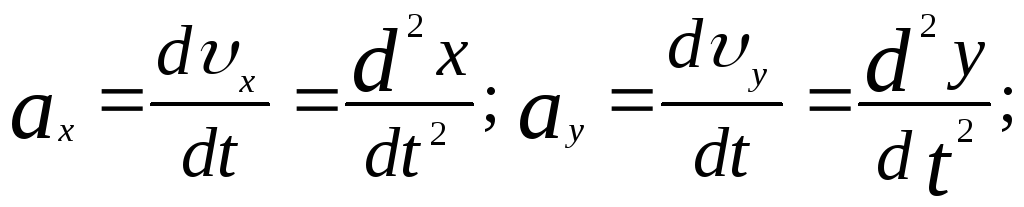
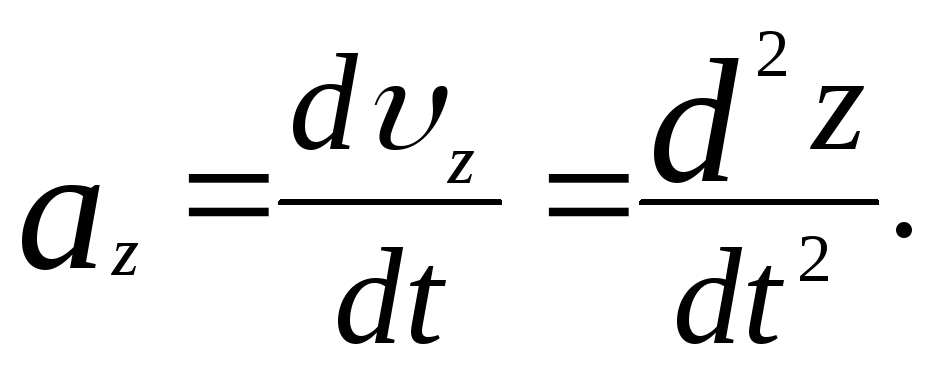(1.31)