2.8. Потенцiальна енергiї

Потенцiальною енергiєю називається енергiя взаємодії тiл (або їх частин), що залежить вiд їх взаємного розташування.

Загалом взаємодiя мiж тiлами вiдбувається або при безпосередньому контактi, або на вiдстанi, за рахунок сил поля. Сили за їх властивостями можна подiлити на два класи. Для сил одного класу робота при перемiщеннi тiла мiж двома точками не залежить вiд траєкторiї руху, а для сил другого класу — залежить вiд траєкторiї руху тiла.

Сили, робота яких не залежить вiд форми траєкторiї руху тiла i визначається тільки початковою i кiнцевою точками траєкторiї, називаються консервативними (наприклад гравiтацiйна сила, електростатична сила). Саме цi сили можна описати за допомогою потенцiальної енергii.

Сили, робота яких залежить вiд траєкторiї руху тiла, називаються неконсервативними (наприклад, сили тертя). Для цих сил не iснує поняття потенцiальної енергiї.

Область простору, в якiй дiють сили, називається полем сил (або просто полем). Поля, в яких дiють консервативнi сили, називаються потенцiальними полями. Тiло, що перебуває в потенцiальному полi, має потенцiальну енергiю .

За означенням, потенцiальна енергiя тiла в даному його положеннi чисельно дорiвнює роботi, яку виконують дiючi на тiло консервативнi сили при перемiщеннi його з цього положення в те, де потенцiальна енергiя умовно приймається рiвною нулю. З цього означення можна зробити два висновки.

По-перше, робота консервативних сил, що дiють на тiло в потенцiальному полi, дорiвнює зменшенню потенцiальної енергiї тiла. Дiйсно, оскільки пiд дiєю консервативних сил тiло перемiщується з точки з бiльшою потенцiальною енергiєю в точку з меншою потенцiальною енергiєю- (поки воно не перемiститься в точку, де = 0), то

(2.69)

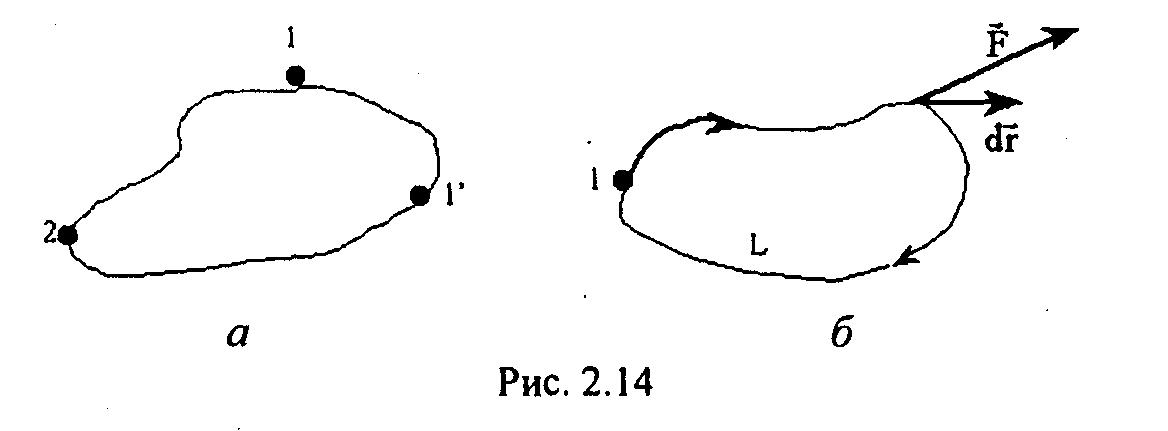
По-друге, значення потенцiальна енергiя залежить вiд того, яке положення тiла умовно взяте за нуль (вибiр нульового рiвня потенцiальної енергiї називається нормуванням потенцiальної енергії). Причому в разi замiни одного нульового рiвня на iнший потенцiальна енергiя змiнюється на сталу величину. Наприклад, вiзьмемо за нульове положення тiла в точцi l (рис.2.14,а). Тодi в положенні 2 потенцiальна енергiя тiла дорiвнюватиме . Якщо ж узяти за нульове положення тiла в точцi l, то його потенцiальна енергiя в точцi 2 буде . Оскiльки сили консервативні, то робота вздовж траєкторiї 2-l дорiвнює роботi вздовж траєкторiї 2 — 1 — l, тобто , або

Роботу А, можна позначити як довiльну константу С i записати в загальному виглядi

(2.70)

Таким чином, потенціальна енергiя визначається не однозначно, а з точнiстю до довiльної сталої. Довiльнiсть вибору сталої не впливає на фiзичнi висновки, оскiльки вони характеризуються не абсолютним значенням потенцiальної енергiї, а й змiною, а саме . Зрозумiло, що для зручностi найчастiше покладають С = 0.

Потенцiальна енергiя залежить вiд характеру взаємодiї тiл, тому єдиної формули для неї, як для кiнетичної енергiї, немає. Крiм того, оскiльки початок вiдлiку вибирається довiльно, потенцiальна енергiя може мати вiд’ємнi значення (кiнетична енергiя завжди додатня). Наприклад, якщо за нуль прийняти потенцiальну енергiю тiла, що пребуває на поверхнi Землi, то потенцiальна енергiя тiла, пiднятого на висоту h₁ буде , а тiло, що перебуває на днi шахти глибиною h₂, буде .

Запишемо тепер математичний критерiй (тобто ознаку) потенцiальностi поля консервативних сил. Нехай тiло рухалося замкненою траєкторією 1—1 (рис.2.14,б). Оскiльки на нього дiяли консервативнi сили, їх робота в цьому замкненому контуру (позначимо його L) дорiвнює нулю. Математично це записується, з урахуванням рiвняння (2.46), так:

.

У математиці інтеграл вигляду називається циркуляцiєю вектора вздовж замкненого контура L. Отже для поля консервативних сил маємо такий математичний критерiй його потенцiальностi:

, (2.71)

тобто циркуляцiя вектора сили по довiльному замкненому контуру L дорiвнює нулю.