Моменты инерции сечений

Моменты инерции подразделяются на осевые, полярные и центробежные.

Осевым моментом инерции сечения относительно некоторой оси называется сумма произведений площадей бесконечно малых площадок на квадраты расстояний до этой оси:

(8)

Полярным моментом инерции сечения относительно некоторой точки (полюса) называется сумма произведений площадей бесконечно малых площадок на квадраты их расстояний до этой точки.

(9)

Центробежным моментом инерции относительно некоторых двух взаимно перпендикулярных осей называется величина:

(10)

Суммирование в формулах (8)-(10) производится по площади сечения А. Размерность моментов инерции есть длина в четвертой степени, т.е. см⁴, м⁴ и т.д.

Как видно из определения (8)-(10) моменты инерции зависят от размера и формы плоской фигуры, а также от выбора системы координат. Согласно данному определению величины осевых и полярных моментов инерции всегда положительны!!! Это следует из исходного определения (8) и (9).

Если полюс берется в начале координат системы z o y (что в дальнейшем всегда предполагается), то

и

.

Таким образом . (11)

Из формулы (10) определяющей центробежный момент инерции следует, что центробежные моменты инерции могут быть положительными, отрицательными или равными нулю. Центробежный момент сечения относительно осей, из которых хотя бы одна является осью симметрии, равен нулю.

После первоначального знакомства с новыми объектами следует подробнее изучить их свойства. Только так можно понять, как их можно использовать в дальнейшем.

Прежде всего, как и статические моменты, моменты инерции обладают свойством аддитивности – моменты инерции всей фигуры равны сумме или разности моментов инерции составных частей.

(12)

Примеры вычисления моментов инерции для простых сечений

1.Прямоугольное сечение:

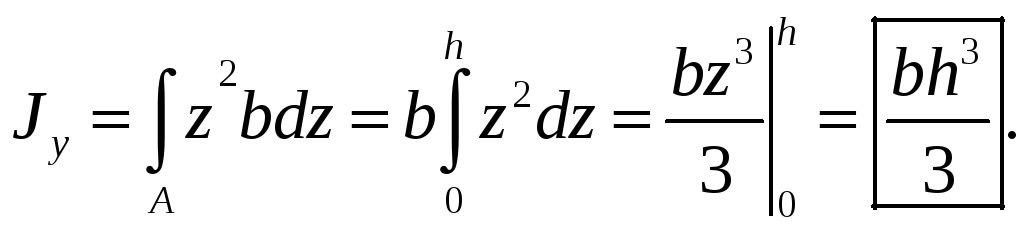
Аналогично:

.

Центробежный момент инерции: .

2.Треугольное сечение:

;

3.Круглое сечение:

.

Переходим к полярной системе координат:

;

;

Тогда

Относительно любой оси, проходящей через центр круга, осевой момент инерции будет одинаков Полярный момент инерции круга

.

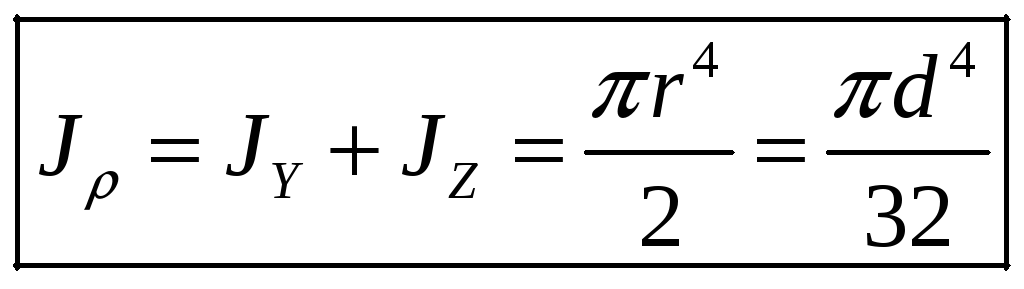Лекция №11 Геометрические характеристики плоских сечений (продолжение)

Изменение моментов при параллельном переносе осей

При решении практических задач приходится определять моменты инерции сечений относительно различных осей. В связи с этим не обязательно определять моменты инерции в новых осях путем интегрирования. Можно использовать значения моментов инерции в других осях. Поэтому очень важно установить зависимости между моментами инерции одной и той же фигуры относительно осей «старой» и «новой» системы прямоугольных координат. Переход от любой старой к любой новой системе координат может рассматриваться как два вида последовательных преобразований старой системы координат.

1) Путем параллельного переноса ее в новое положение.

2) Путем поворота ее относительно нового начала координат.

Выясним, как изменяются моменты инерции при параллельном переносе осей. Пусть моменты инерции в старой системе координат известны. Возьмем новую систему координат , оси которой параллельны прежним осям.

Выразим координаты элемента площади в новой системе через координаты в старой системе.

Тогда согласно исходному определению моментов инерции (8) и (10) имеем:

,

,

но .

Тогда получаем: . (12)

Если старые оси и проходят через центр тяжести сечения (центральные оси), то , и тогда

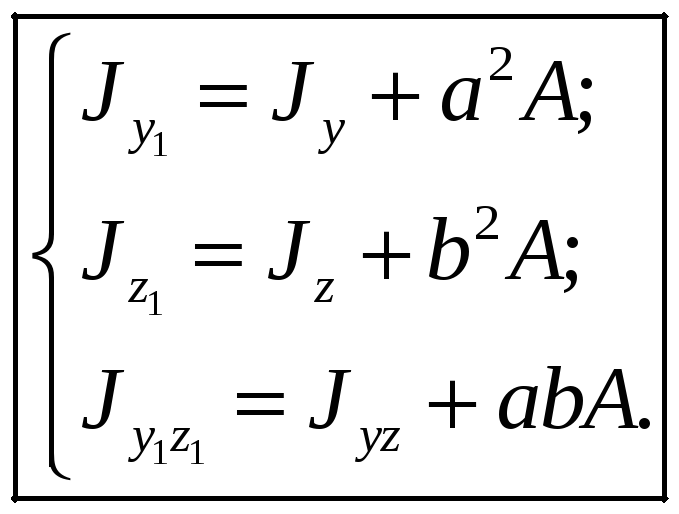(13)

На основании (13) делаем следующий вывод. Из всех параллельных друг другу осей осевой момент инерции имеет наименьшее значение относительно оси, проходящей через центр тяжести сечения. То есть чем дальше ось от центра тяжести, тем больше осевой момент инерции. Таким образом, центральные оси обладают свойством оптимальности в смысле минимальности осевых моментов. Именно поэтому в поперечных сечениях брусьев вводятся центральные оси.

Если одна из старых осей координат совпадает еще и с осью симметрии сечения, то и тогда

. (14)

Рассмотрим примеры применения параллельного перехода.

Моменты инерции прямоугольника относительно осей вычислены путем непосредственного интегрирования (8), (10). Определим моменты инерции относительно осей симметрии . Для этого воспользуемся алгоритмом (13).

откуда выражаем:

Интегрированием ранее получен результат: .

Выразим на основании (13)

.

Также получим:

.

Если треугольник будет равнобедренным, то и ось становится центральной. В таком случае .

Изменение моментов инерции при повороте осей

Предполагаем известными моменты инерции данного сечения в системе координат . Далее возьмем другую систему координат , повернутую на угол относительно прежней. Запишем формулы преобразования координат при повороте осей:

(16)

Далее выражаем:

(17)

Учитывая, что , то можно записать:

(18)

Оказывается, что при повороте осей координат осевые моменты изменяются, но их сумма остается постоянной.

(19)