Лекция №6
РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
Прямолинейные брусья, нагруженные силами, которые приводятся к продольной оси, называются стержнями.
В силу характера нагружения в поперечных
сечениях стержней из шести возможных
внутренних силовых факторов нулевой
один – внутренняя продольная сила
.
Представление о характере деформирования
стержней можно получить из опытов. В
достаточном удалении от нагруженных
концов стержня плоские сечения до
деформации остаются плоскими и в
результате нагружения. Депланация
(искривление) сечений наблюдается в
непосредственной близости от места
приложения нагрузок. Но стоит отойти
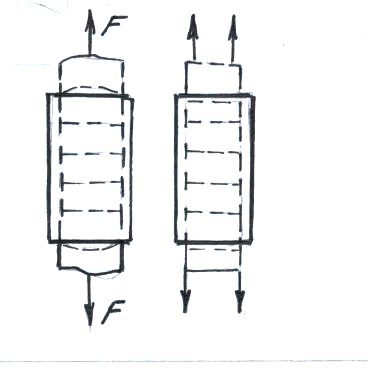
от точек приложения на расстояния сравнимые с поперечными размерами стерня как депланация практически исчезает. В этом заключается суть гипотезы Бернулли. Таким образом, можно считать, что в большей части достаточно длинных стержней напряженно-деформированное состояние однородным (равномерным) в пределах поперечных сечений.
Это значит, что расстояние между
точками соседних сечений поперечных
сечений изменяются одинаково. Поэтому
и продольная деформация по всему сечению
будет одинакова. Т.к. напряжение
зависит от деформации, то и оно по сечению
не изменяется.
Т.к.
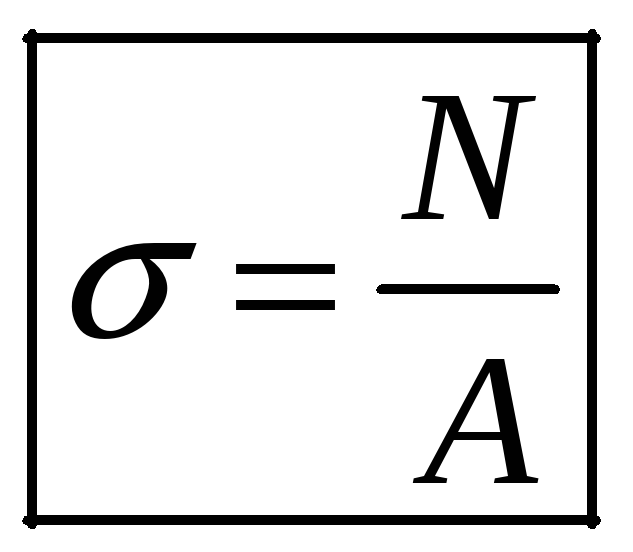формула для определения нормальных
напряжений в поперечных сечениях
стержней.
ПРОДОЛЬНАЯ И ПОПЕРЕЧНАЯ ДЕФОРМАЦИИ
-
абсолютная продольная деформация
-
абсолютная поперечная деформация
-
относительная продольная деформация
- относительная поперечная деформация
Связь между продольной и поперечной деформациями:
-
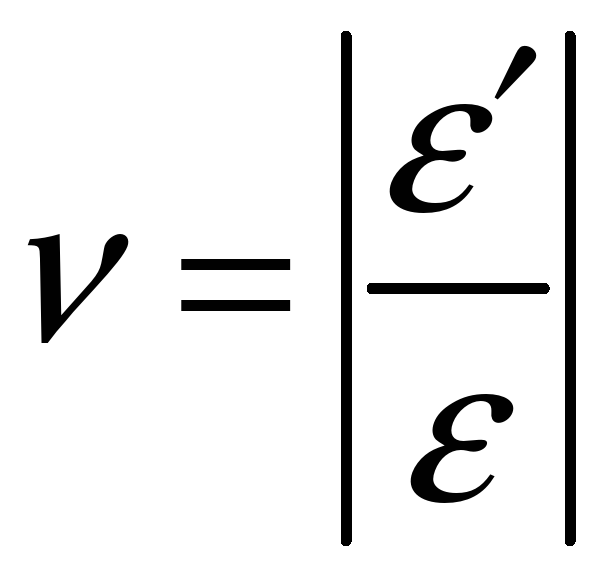коэффициент Пуассона
НАПРЯЖЕНИЯ В НАКЛОННЫХ СЕЧЕНИЯХ СТЕРЖНЯ
Напряжения в поперечных сечениях стержня
с помощью гипотезы плоских сечений
удалось установить достаточно просто.
Это формула нормального напряжения
,
а касательное напряжение
.
Теперь возникает вопрос. А что происходит
во всевозможных наклонных сечениях,
проходящих через одну точку с поперечным
сечением? То есть, какие напряжения
действуют в наклонных сечениях стержня?
Для этого рассмотрим стержень
постоянного сечения, нагруженный
внешними силами в концевых сечениях. В
таком случае напряженное состояние в
стержне будет однородным. А именно, в
сечениях одинаковой ориентации, но
проходящих через разные точки на
продольной оси, распределение напряжений
(характер действия) будет одинаковым.
Сказанное позволяет, например, считать,
что сечения
и
проходят
через одну точку.
Поперечное
и наклонное
сечения выделяют из стержня элемент
.
Действие «отброшенных» частей в
поперечном сечении заменяется
напряжением
,
а в наклонном сечении нормальным
напряжением
и касательным
.
Причем
и
,
так же как и
предполагаются равномерно распределенными
по сечению.
Далее пусть площадь поперечного
сечения
равна
.
Тогда площадь наклонного сечения
.
Запишем условия равновесия выделенного
элемента
.
Так как имеем плоскую систему сходящихся
в одной точке сил, то:
После подстановки
и сокращения на
получаем систему двух уравнений
относительно
и
:
или
Решением является
(1)
(2)
Полученные формулы (1) и (2) следует
понимать так: если известны напряжения
(собственно только
)
в поперечном сечении стержня, то
напряжения (это
и
)
в любом наклонном сечении, проходящего
через ту же точку на продольной оси,
можно вычислить. Вот почему из множества
сечений бруса можно рассматривать (в
плане определения напряжений) только
одно – а именно поперечное сечение.
Теперь следует проанализировать
изменение напряжений
и
при переходе от сечения к сечению (т. е.
с изменением угла
).
Из
(т. к.
при
),
то есть нормальные напряжения достигают
максимума в поперечных сечениях. Так
как
,
при
.
Касательное напряжение в поперечных
сечениях отсутствует.
При
В продольных сечениях стержня при его
растяжении или сжатии напряжения не
возникают.
Определим
и сечение где оно действует. Решаем
задачу экстремума для функции (2):
.
Главные значения
На площадках под углом
к оси стержня действуют максимальные
касательные напряжения.
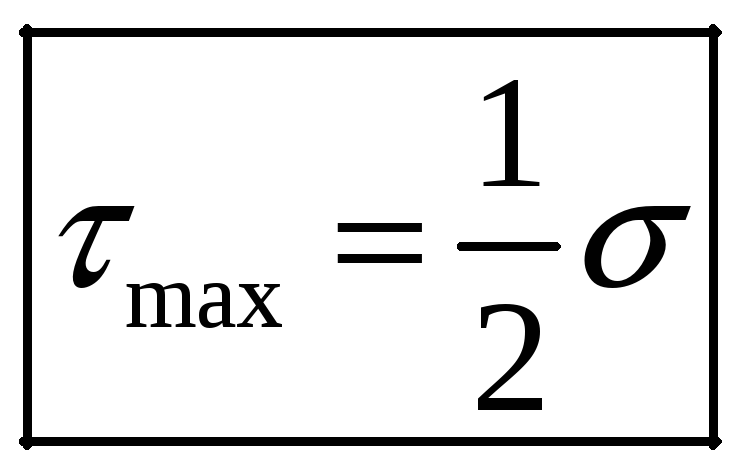
ПЕРЕМЕЩЕНИЯ ПОПЕРЕЧНЫХ СЕЧЕНИЙ
В результате деформации стержня под действием приложенных к нему внешних сил происходит смещение поперечных сечений друг относительно друга.
В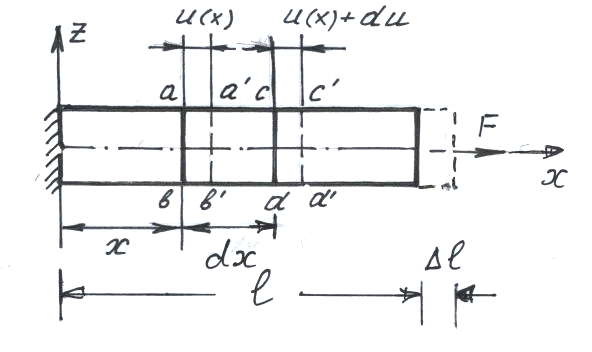
стержне до нагружения возьмем два
бесконечно близкие поперечные сечения
и
.
Их исходные координаты
и
.
Согласно гипотезе плоских сечений
поперечные сечения в процессе нагружения
стержня остаются плоскими и параллельными
друг другу. Они лишь перемешаются
относительно исходного положения в
направлении продольной оси (оси
).
Такое перемещение принято обозначать
символом
(таким образом
(
)
- продольное перемещение сечения с
координатой
).
Перемещение бесконечно близкого сечения
равно
.
Если
(
)
перемещение сечения
является следствием деформации фрагмента
стержня длиною
,
то перемещение сечения
результат деформации фрагмента длиною
.
Определим деформацию элемента
стерня
.
Его исходная длина до приложения внешних
сил
.
После приложения внешних сил
.
Или
.
Тогда абсолютная деформация этого
элемента
.
Относительная деформация элемента
.
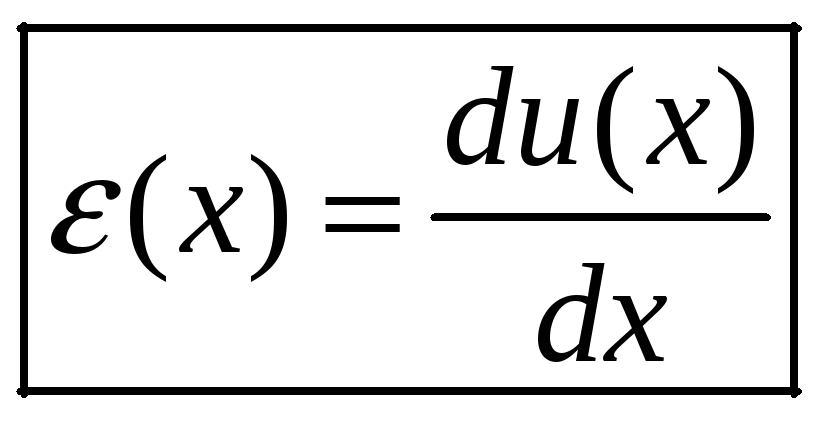То есть относительная продольная
деформация стержня в сечении с координатой
равна скорости изменения (производной)
функции продольного перемещения сечения.
Откуда
,
и тогда
.
Для новичка последняя формула может
показаться страшной, но в ней заключен
простой смысл: продольное перемещение
произвольного поперечного сечения
стержня определяется деформацией
участка стержня справа от сечения.
Константа
учитывает возможное перемещения стержня
как жесткого тела и определяется из
условия, что
.
Если в сечении
стержень закреплен, то
.
Поскольку
(вспомним диаграмму
),
то
.
Если материал подчиняется линейному
закону Гука (т. е. стержень нагружается
до напряжения предела пропорциональности
),
то
и
.
Если на участке стержня
,
то
.
Относительное смещение
концов стержня
и
равно
.
А учитывая что
,
получаем 
.
Это самая общая формула вычисления
абсолютной продольной деформации
стержня. Если по длине стержня
и
,
то есть стержень постоянного сечения
нагружен внешними силами только в
концевых сечениях, то
.
-
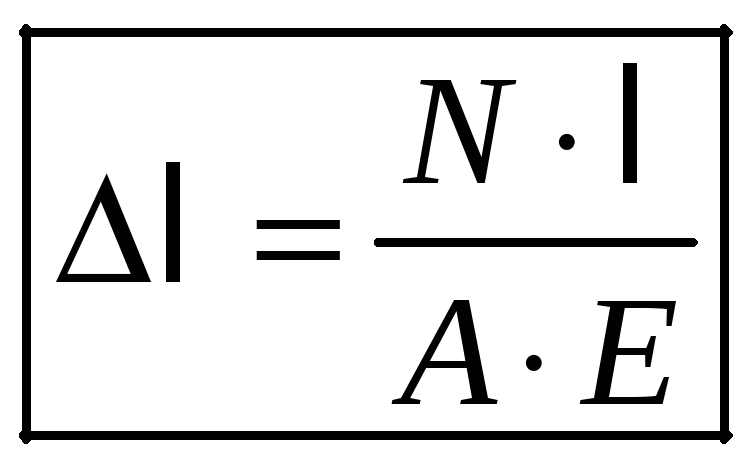жесткость сечения стержня на растяжение
или сжатие.
Две последние формулы представляют развернутую запись закона Гука для стержня.
ЭНЕРГИЯ ДЕФОРМАЦИИ СТЕРЖЯ
Пусть материал стержня подчиняется
линейному закону Гука. Во всяком случае,
будем считать, что нагружение производится
до той стадии, когда еще не нарушается
линейная зависимость
.
При нагружении стержня, в результате его упругой деформации происходит накопление потенциальной энергии. Это та энергия, которая при разгрузке высвобождается и может совершить работу (подобно растянутой или сжатой пружине).
Если не брать в учет рассеяние энергии
в виде выделения тепла и электромагнитного
излучения, то энергия деформации
будет
численно равна работе внешних
сил
согласно закону сохранения энергии.
Вычислим работу внешней силы
,
которая приложена к стержню длиной
и поперечного сечения
.
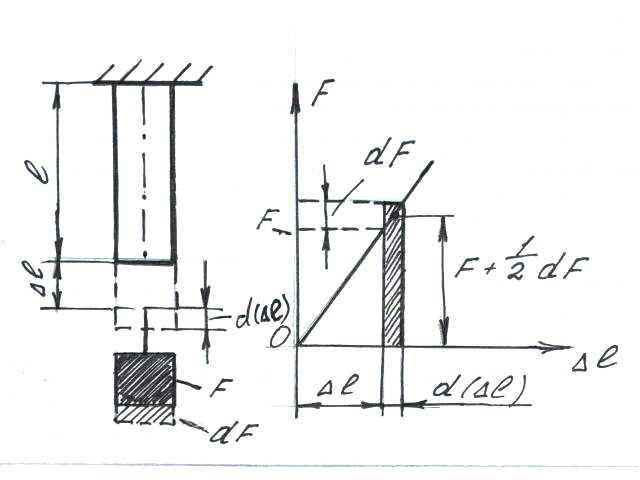Если к стержню приложить центральную
силу, постепенно возрастающую от нуля
до некоторого значения
,
то стержень получит деформацию (удлинение
или укорочение)
.
Добавляя к силе
бесконечно малое значение
,
деформация также получит приращение
.
Следовательно, сила
,
получает перемещение
,
и на этом перемещении она совершает
работу
.
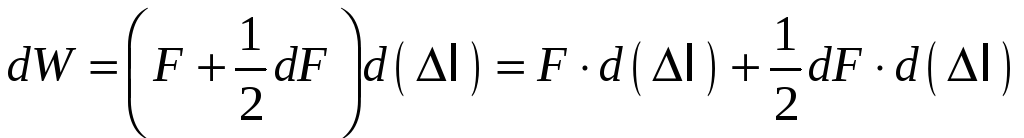Пренебрегаем величиной 2-го порядка малости, по сравнению с величиной 1-го порядка малости. Тогда
Согласно закону Гука
,
и, вычисляя дифференциал, получаем
.
При изменении силы от нуля до некоторого
значения
она
совершает работу
.
Или при учете закона Гука
,
т. е. если сила сама создает упругое
перемещение точки приложения, то ее
работа на этом перемещении вычисляется
с коэффициентом 1/2.
Тогда согласно закону сохранения энергии
.
Пусть стержень нагружен различными
центральными силами по его длине. Таким
образом, внутренняя сила
может изменяться от сечения к сечению,
т.е.
.
Вычислим деформацию энергию деформации
такого стержня. Выделим в пределах
стержня элемент бесконечно малой длины
.
Взамен «отброшенных» левой и правой
частей введем в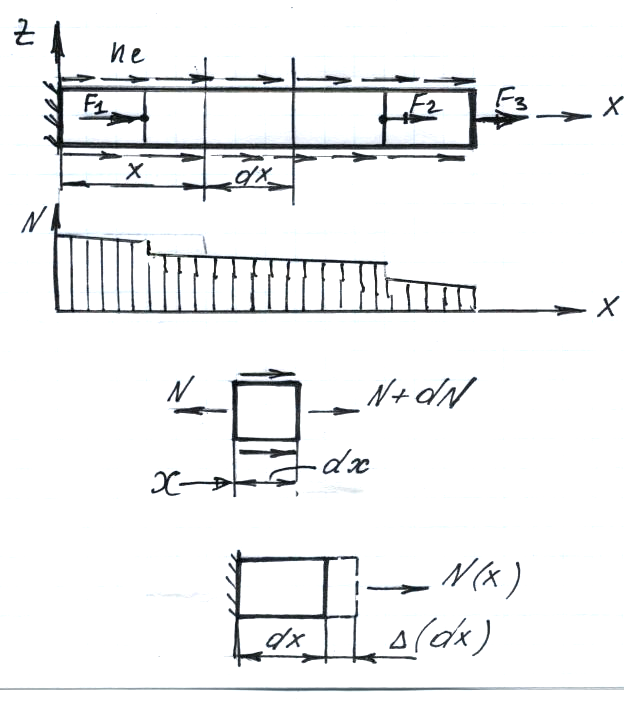
сечении с координатой
силу
,
а в сечении с координатой
силу
(т. к. сечения бесконечно близкие, то и
внутренняя сила в них отличается на
бесконечно малую величину). В силу
малости
можно пренебречь влиянием внешней
распределенной нагрузки
на внутреннюю силу
в пределах рассматриваемого элемента.
Тогда если закрепить левое сечение
элемента, а на правом сечении приложить
внешнюю силу
,
то выходим на случай рассмотренный
только что. То есть имеется стержень
длины
постоянного сечения
и нагруженный на конце сосредоточенной
силой
.
Вычислить накопленную потенциальную
энергию при деформации элемента можно
по формуле, полученной ранее:
.
Тогда потенциальная энергия, накопленная при деформации (нагружении) всего стержня вычисляется суммированием вкладов всех бесконечно малых элементов в пределах длины стержня, то есть интегрированием
.
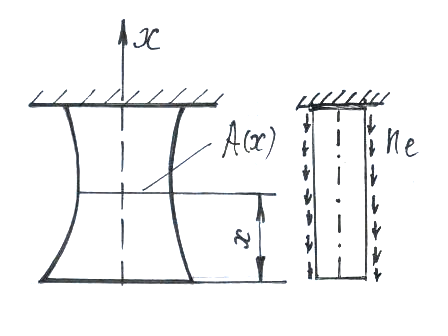
Учет собственного веса стержня
Собственный вес вызывает растяжение или сжатие стержня, когда его ось расположена вертикально. Собственный вес вертикального бруса (например, вытяжной трубы ТЭЦ или вес каната подъемника в шахте) можно рассматривать как продольную внешнюю нагрузку, распределенную вдоль оси.
Интенсивность распределенной нагрузки
по оси бруса в любом сечении
определяется
как
,
где
-
плотность (удельный вес) материала
стержня. Тогда для определения величины
продольной силы
,
действующей в поперечном сечении бруса
,
находим равнодействующую распределенной
нагрузки:
.
Нормальные напряжения в поперечных сечениях бруса определяются так:
.
Для стержня постоянного поперечного
сечения
интенсивность распределенной нагрузки
постоянна по длине бруса
.
Тогда
.
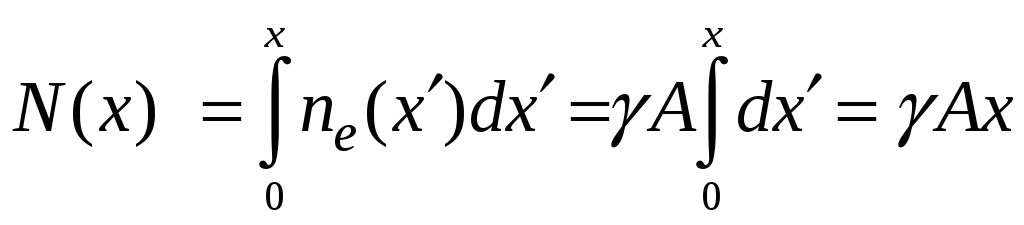И
.
Наибольшая продольная сила и напряжение
возникают в сечении при
.
Если на стержень действуют и другие внешние силы, то они учитываются обычным способом.
РАСЧЕТ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ СТЕРЖНЯ
Основная задача сопротивления материалов - это дать ответ на вопрос о степени надежности деталей машин, различных конструкций и т.д. Под надежностью понимается способность элемента конструкции или всей конструкции функционировать в заданных условиях. В сопротивлении материалов основными параметрами, которые определяют функционирование различных изделий, являются напряжения и деформации. Нормальная работа изделий возможна в определенных границах изменение этих параметров. Когда обеспечивается достаточная прочность и жесткость этих объектов.
Элемент конструкции считается прочным, если под действием внешних воздействий он не разрушается. Прочность элемента, при условии что напряжения, возникающие под действием внешних сил, не превысят определенной величины, т.е. должно выполняться неравенство:
Это неравенство называется условием прочности.
Для обеспечения достаточной жесткости элемента нужно следить за тем, чтобы изменение его геометрических размеров и формы вследствие деформации не превышало заданных значений. При этом записывают неравенство, называемое условием жесткости стержня:
,
либо
.
В первом случае ограничивается деформация стержня в целом, во втором локально.
Величины, стоящие в левых частях записанных неравенств определяются расчетным путем. Справа стоят величины допускаемых напряжений и деформаций.
Допускаемые напряжения
устанавливают
из экспериментов. Простейшие из опытов
это растяжение и сжатие цилиндрических
образцов из различных материалов. Так
подвергая, растяжению образец из
малоуглеродистой стали (сталь3) можно
построить диаграмму (график зависимости)
,
характеризующую прочность и пластические
свойства материала.
-
предел пропорциональности (proportionality)
-
предел упругости (elasticity)
-
предел текучести (yield)
-
временное сопротивление растяжению
(ultimate)
предел прочности при растяжении
-
упругая деформация (elastic)
-
остаточная деформация (residual)
Аналогичные опыты проводят и с другими материалами и при других видах нагружения (сжатие, например)
Таким образом, устанавливаются опасные
напряжения
.
Если, например, деталь в процессе
эксплуатации не должна в деформированном
состоянии выходить за режим пластической
деформации, то
Если же пластические деформации не
представляют опасности, то нужно
обеспечить целостность элемента. В этом
случае
.
Для хрупких материалов пределы прочности при растяжении и сжатии различны. И тогда
,
.
Опасные напряжения это еще не
.
Связь между ними
,
где
-
коэффициент запаса прочности. Этот
коэффициент выбирается с расчетом,
чтобы был обеспечен достаточный запас
прочности на тот случай, когда могут
проявить себя различные неучтенные
факторы, как временный всплеск нагрузок,
влияние внешних условий эксплуатации.
Этот коэффициент призван учитывать
приближенный характер вычисляемых
напряжений и разброс в определении
.
В связи с этим, в качестве
принимаются
уменьшение в
раз.
На практике величина колеблется в
пределах от 1,7-1,8 до 8 – 10 и зависит
от условий работы конструкции. Другими
словами
.
-
при наступлении текучести пластичного
материала, как при растяжении, так и при
сжатии;
-
предел прочности при растяжении хрупких
или пластичных материалов;
-
предел прочности при сжатии упругих
материалов.
Допускаемая деформация
и
- выбираются исходя из функционального
назначения того или иного элемента.
Из удовлетворения условиям прочности и жесткости могут быть подобраны соответствующие для данного случая нагрузки, геометрические размеры или материал.
Например, известен материал, из которого
изготовлен стержень
и
нагрузки. Требуется установить оптимальный
размер площади сечения
.
Решается, например, только задача
прочности:
;
;
.
Значение
берется с эпюры
,
которая предварительно строится.