Лекция 7

РАСТЯЖЕНИЕ, СЖАТИЕ СТЕРЖНЕЙ. РАСЧЕТ НА ПРОЧНОСТЬ.

Брус с прямолинейной осью, подверженный действию внешних сил вдоль оси (и равнодействующая которых действует вдоль оси бруса и приложены в центре тяжести сечения) называется стержнем. Такой вид нагружения называется центральным растяжением или сжатием.

Рис.

В стержнях под действием продольных внешних сил в каждом из поперечных сечений возникает только один силовой фактор – внутренняя продольная сила. Как нам уже известно, эта внутренняя продольная сила определяется с помощью метода сечений. Эпюры продольных усилий мы умеем строить.

Продольные и поперечные деформации при растяжении (сжатии).

Рассмотрим прямой брус длиной , заделанный одним торцом и нагруженный на другом торце растягивающей силой F. Под действием силы F брус удлиняется на некоторую величину . Эта величина называется полным или абсолютным удлинением (абсолютная продольная деформация). Она имеет размерность длины. Отношение абсолютной деформации к первоначальной длине бруса называется относительной деформацией.

( 1 )

Рис.

Относительная деформация величина безразмерная. Деформация положительная, если стержень удлиняется. Отрицательная, если стержень сжимается.

Интуитивно понятно, что чем больше величина приложенной силы, тем больше деформация стержня; и чем больше площадь напряженного сечения бруса, тем деформация меньше. Стержни из различных материалов деформируются по- разному. Из опыта установлена следующая зависимость для деформации стержня:

( 2 )

где N- внутренняя продольная сила; F - площадь поперечного сечения; E - коэффициент, зависящий от физических свойств материала. Так как

( 3 )

получаем ( 4 )

или

( 5 )

Формула (5) представляет математическую запись закона Гука. Впервые этот закон был сформулирован в 1660г. Р.Туком. E - модуль упругости материала. Он представляет коэффициент пропорциональности между напряжением и деформацией. Это физическая постоянная материала, характеризующая его способность сопротивляться упругому деформированию, или короче, характеризующая жесткость материала.

Величина EF называется жесткостью сечения при растяжении и сжатии.

Абсолютное удлинение можно записать:

( 6 )

это развернутая запись закона Гука.

При действии на стержень продольной силы появляется не только продольная деформация (деформация вдоль линии действия силы), также наблюдается и поперечная деформация, т.е. деформация в направлении перпендикулярном линии действия силы. При растяжении стержня поперечный размер уменьшается, при сжатии увеличивается.

Рис.

- абсолютная поперечная деформация;

( 7 )

- относительная поперечная деформация.

Как явствует из опыта относительная поперечная деформация прямо пропорциональна продольной деформации, но с обратным знаком

( 8 )

коэффициент зависит от материала: он называется коэффициентом поперечной деформации или коэффициентом Пуассона

( 9 )

Коэффициент Пуассона и модуль упругости E характеризуют упругие свойства материала:

Напряжения в сечениях стержня

В стержне нагруженном осевой продольной силой, в поперечных сечениях напряжение определяется по формуле .

Рис.

В сечениях расположенных под некоторым углом к оси стержня, напряжения будут отличные от .

Рис.

Как мы выяснили ранее в сечении с нормалью действует полное напряжение , которое можно представить в виде суммы нормального и касательного .

Рассмотрим элемент малой длины l. Он находится в равновесии под действием напряжений , и .

Если F площадь сечения mn, то площадь наклонного сечения pq

( 10 )

Запишем условие равновесия элемента mп pq.

( 11 )

Учитывая (10) и (11) получим

( 12 )

Разрешая эту систему получим:

( 13 )

Из (13) видно, что нормальные и касательные напряжения зависят не только от , но и от ориентации площадки. Из (13) также видно. Что убывает при увеличении угла от 0 до ; тогда как обращается в ноль при и . Своего максимального значения касательные напряжения достигают на площадках :

Перемещение поперечных сечений

Приложенные к стержню продольные силы вызывают в нем деформации. Кроме того, при деформировании поперечные сечения перемещаются друг относительно друга.

Рис.

Пусть OX направлен по оси стержня. Сечение ab до деформации имеет координату X, а сечение cd координату . После приложения нагрузки сечение ab перейдет в положение , получив перемещение , а сечение cd – в положение , получив перемещение , т.е. .

Длина вырезанного элемента до деформации: после деформации стала . Удлинение его равно Относительная деформация представляет: . Привлекая закон Гука:

получим . Интегрируя это соотношение получим:

,

E- и - .

Учет собственного веса стержня

Собственный вес вызывает растяжение или сжатие стержня, когда его ось расположена вертикально. Собственный вес вертикального бруса можно рассматривать как продольную внешнюю нагрузку, распределенную вдоль оси.

Рис.

Интенсивность распределенной нагрузки по оси бруса в любом сечении X определяется как , где - плотность материала. Тогда для определения величины продольной силы , действующей в поперечном сечении бруса X находим равнодействующую распределенной нагрузки:

Нормальные напряжения в поперечных сечениях бруса определяются так:

Для стержня постоянного поперечного сечения интенсивность распределенной нагрузки постоянная по длине бруса

Тогда

И

Наибольшая продольная сила и напряжение возникают в сечении при

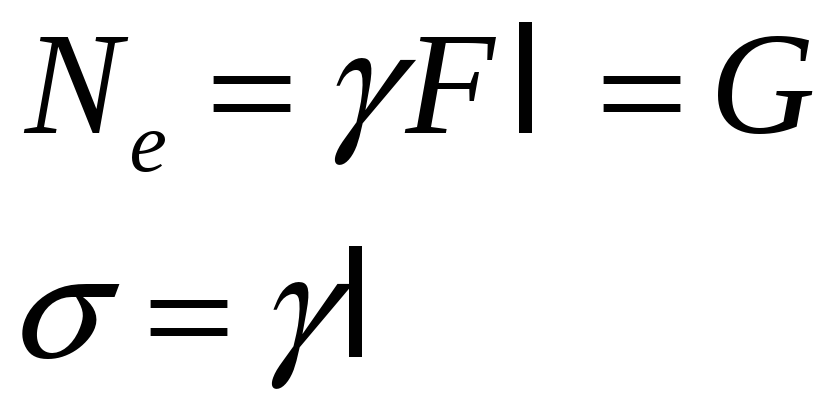
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ СТЕРЖНЯ

Рассмотрим нагружение стержня силой . Предполагаем, что сила статическая, т.е. она нарастает постоянно. Сила вызывает продольную деформацию стержня. Сечение где она приложена смещается на величину

Перемещаясь вместе с сечением сила совершает работу.

На перемещении сила совершает работу

На диаграмме . Полную работу при изменении силы от до определяем:

Если напряжение в брусе при нагружении силой не превосходит то есть площадь треугольника с высотой и основанием , которое по закону Гука равно

В этом случае:

При нагружениях не превышающих предела упругости, можно пренебречь потерями энергии в виде тепла и электромагнитного излучения и поскольку нагрузка статическая можно не учитывать кинетическую энергию стержня. Вследствие этого вся работа внешних сил, на основании закона, на основании закона сохранения энергии переходит в потенциальную энергию деформации бруса.

; ;

РАСЧЕТ НА ПРОЧНОСТЬ. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ.

Наибольшие напряжения, возникающие в элементах сооружения при его эксплуатации, должны быть меньше некоторых продольных (опасных значений напряжений, зависящих от свойств материалов. При достижении рабочими напряжениями предельных значений прочность элемента сооружения будет нарушена. Под нарушением прочности понимается не только разрушение, но и возникновение пластических деформаций. Под расчетом на прочность понимается следующее. Каждый элемент сооружения будет нормально выполнять свою функцию только при выполнении условия прочности. Так подбираются размеры элемента при известных нагрузках или подбираются нагрузки по данной геометрии. В любом случае этот подбор ведется из удовлетворения условию прочности.

Относительно допускаемого напряжения следует сказать, что:

1. Он зависит от применяемого материала.

2. Он зависит от требований, которые предъявляются к сооружению.

Вопрос о выборе допускаемого напряжения очень важен. При правильном его выборе возможно либо преждевременное разрушение сооружения, либо перерасход материала.

Для пластичных материалов

Для хрупких материалов ,

Где и - коэффициент запаса прочности.

Величины коэффициента запаса прочности устанавливаются при разработке норм с учетом целого ряда обстоятельств.

Лекция 8

Статически неопределимые задачи

До настоящего момента мы имели дело с задачами, в которых все внутренние усилия от заданной внешней нагрузки могли быть определены при помощи только уравнений равновесия (уравнений статики). Такие задачи (или системы) называются статически определимыми. Приведем некоторые простейшие примеры.

Пример 1.

В данном случае задача решается при помощи только уравнений равновесия, т.е. усилия в любом сечении стержня мы определяем, составляя уравнения равновесия любой части от сечения

.

Напряжения определяются соответственно

.

В статически определимых задачах при расчете на прочность нам не нужна информация о деформации стержня, т.к. напряжения мы находим, зная только усилие.

Пример 2.

Абсолютно жесткая балка АВ подвешена на двух упругих стержнях (1 и 2). Полагаем, что стержни соединены с опорой и балкой АВ шарнирно. Это означает, что в стержнях будут возникать только продольные усилия. Наша задача определить эти усилия ( и ). Для их определения запишем уравнения равновесия:

.

Задача, таким образом, решена. Наряду со статически определимыми системами в инженерной практике часто встречаются системы усилия и напряжения, в которых не могут быть определены при помощи одних лишь уравнений равновесия. Такие системы (или задачи) называются статически неопределимыми. Само название говорит за себя. При расчете на прочность статически неопределимых систем к уравнениям равновесия требуется составлять дополнительные уравнения. Смысл этих дополнительных уравнений состоит в том, что рассматриваются перемещения системы, которые получаются как результат деформации отдельных элементов системы. Поскольку при действии нагрузок на каждый элемент системы будут передаваться усилия, в результате появляется деформация этих элементов. Но все элементы соединены в единую систему. Значит должна существовать вполне определенная связь между деформациями отдельных элементов. Так вот, уравнения связывающие деформации отдельных элементов и будут дополнительными уравнениями. Они так и называются – уравнения совместности деформаций (уравнения неразрывности или уравнения перемещений).

Число дополнительных уравнений, необходимых для решения статически неопределимой задачи, характеризует степень её статической неопределимости. Всегда можно составить необходимое количество дополнительных уравнений. Итак, степень статической неопределимости определяется как разность числа неизвестных реакций или усилий, и числа уравнений равновесия, которые можно составить.

Пример 3.

Рассматриваемый стержень закреплен с двух сторон, т.е. на каждом из торцов будет действовать неизвестная реакция: и . С другой стороны для определения этих реакций мы имеем только одно уравнение равновесия: .

Для решения этой задачи (т.е., чтобы определить усилие в любом сечении стержня) требуется составить одно дополнительное уравнение. Следовательно, задача является один раз статически неопределимой. Дополнительное уравнение в данном случае можно составить из следующих соображений. Отбросим нижнюю заделку, и действие её заменим реакцией . Тогда:

По закону Гука: .

Деформация участков:

Но деформация стержня складывается из деформаций участков составляющих его: . Получим уравнение совместности деформаций. Или

. Отсюда: .

Знак «минус» говорит о том, что направление реакции противоположное.

.

Теперь можно построить эпюру N.

Пример 4.

Введение дополнительного стержня 3 сделало нашу предыдущую систему (пример 2) один раз статически неопределимой. Составим уравнения равновесия:

В два уравнения входит 3 неизвестных. Значит, задача однажды статически неопределима. Как записать дополнительное уравнение? Балка АВ абсолютно жесткая, поэтому при действии силы F она изменит свое положение за счет деформации стержней. При этом деформация каждого стержня будет зависеть от деформации других стержней. Другими словами между деформациями стержней должна существовать определенная зависимость.

Задается любая кинематически возможная деформация системы. То есть такая деформация, при которой не нарушаются внешние связи и все стержневые элементы сохраняют целостность. И еще один важный момент – деформация конструкции считается настолько малой, что можно не учитывать некоторые эффекты. В нашем примере в деформированном состоянии конструкции стержни 1,2,3 остаются параллельными.

В нагруженном состоянии стержень АВ занимает новое положение . Стержни получают деформацию:

Уравнения совместности деформаций составим из геометрических соображений. Т.к. , то . И так как , то

но и тогда

Последнее уравнение это и есть уравнение совместности деформаций в рассматриваемой конструкции. Поскольку конструкция один раз статически неопределима, то стержни не могут получать произвольные деформации независимо друг от друга. Деформации стержневых элементов должны быть согласованы между собой.

Используя физическое соотношение (закон Гука) получим:

Еще один важный момент. По ходу решения задачи приходится дважды делать предположения по поводу знаков усилий в стержнях и знаков деформаций. Первый раз когда вводятся реакции внешних связей. Проще вводить реакции, которые соответствуют растяжению стержней (направление от стержня соответствует растяжению). И эти направления входят в уравнения равновесия.

Второй случай это выбор кинематически возможной деформации конструкции, при которой стержни могут, как растягиваться, так и сжиматься. При записи закона Гука для каждого стержня необходимо согласовывать знаки усилия и деформации .

В нашем случае длины стержней одинаковы . Стержни изготовлены из одного и того же материала (сокращаем Е). Далее полагаем, что площади стержней также одинаковы

Получили замкнутую систему уравнений относительно неизвестных усилий

Из (1) выражаем и подставляем в (2): .

И в (3): .

;

Разрешая систему двух последних уравнений, получаем:

Из приведенных примеров можно сделать такой вывод: В статически неопределимых стержневых системах распределение усилий между стержнями зависит от жесткостей стержней. Введем понятие жесткости стержня. Если обозначить , тогда закон Гука для стержня можно записать как . Чем больше жесткость стержня, тем меньшую деформацию он получает при одном и то м же усилии . То есть при повышении жесткости какого-то стержня (увеличение площади, уменьшение длины, увеличение модуля упругости) приводит к увеличению усилия в этом стержне и уменьшению усилий в остальных. В статически же определимых системах распределение усилий в конструкции не зависит от жесткости её элементов.

Eще одна особенность: в статически неопределимых задачах для определения усилий в стержнях необходимо предварительно задаваться размерами их поперечных сечений или их отношениями. Этого не требовалось в статически определимых задачах.

Учет неточности изготовления элементов системы.

Статически неопределимыесистемы имеют ещё очень важную особенность, которую необходимо учитывать на практике. При изготовлении всякого рода сооружений нельзя обеспечить абсолютно точного соблюдения размеров их частей. Поэтому надо считаться с возможностью тех или иных неточностей изготовления. В статически определимых задачах неточности изготовления не вызовут дополнительных напряжений.

Пример 5. Если стержень АВ будет сделан немного длиннее запроектированного (речь идет о долях процента проектной длины), то это поведет за собой лишь небольшое искажение треугольника АВС. При отсутствии силы F в стержнях АВ и АС усилия равны нулю независимо от того, с какой точностью они изготовлены.

В статически неопределимых задачах дело обстоит иначе. Пусть стержень 3 изготовлен на величину короче. Чтобы соединить точку и А необходимо растянуть стержень 3 и сжать стержень 1 и стержень 2. Таким образом, после сборки статически неопределимой системы в ее элементах уже появятся усилия. Такие усилия и напряжения принято называть монтажными. Определим усилия от неточности изготовления.

Схема решения этой задачи не отличается от рассмотренной нами выше. В предположении, что конструкция уже смонтирована, освобождаем ее от внешних связей (т. е. вводим реакции опор). Внутренняя продольная сила в стержне равна реакции опоры, поэтому реакции обозначаем , , . Верхний индекс указывает на то что усилия в стержнях только монтажные. Направления усилий соответствуют растяжению стержней. Прежде всего, записываем уравнения равновесия. Для плоской системы сходящихся сил можно записать только два уравнения статики:

Задача 1 раз статически неопределима. Составим уравнение совместности деформаций. Пусть точки и А нам удалось совместить в точке . Таким образом наши стержни получают упругие деформации:

Чтобы записать уравнение совместности деформаций рассмотрим, например: он в силу малости деформаций прямоугольный (если в процессе деформации конструкции стержень меняет ориентацию, то его абсолютная деформация определяется проецирование короткого состояния на более длинное):

Тогда:

В силу симметрии деформация первого стержня связана с деформаций третьего точно так же. Далее используем закон Гука и выразим уравнение совместности деформации через усилия:

Из уравнения равновесия получаем: .

Пусть

Третий стержень находится в растянутом состоянии, а первый и второй в сжатом. Вычислим напряжения в поперечных сечениях стержней:

А это значительно больше допускаемого напряжения для материала (сталь3 ). В данном случае еще на стадии монтажа конструкции (т. е. до приложения полезной нагрузки) произойдет разрушение стержневых элементов. Величина отклонение от проектного размера третьего стержня является недопустимо большой.

Мы, таким образом, убедились, что неточности изготовления влекут за собой усилия в стержнях даже при отсутствии внешних нагрузок.

ЛЕКЦИЯ 9

Статически неопределимые стержневые системы (продолжение).

Еще пример.

На рисунке (слева) приведена статически определимая стержневая система. Если, например, стержень 1 будет сделан немного длиннее запроектированного, то это вызовет лишь небольшое искажение прямоугольника ABCD. При отсутствии внешней нагрузки усилия в стержнях 1 и 2 равны нулю независимо от того, с какой точностью они изготовлены.

В статически неопределимых задачах дело обстоит иначе. Пусть стержень 3 на величину короче. Чтобы соединить точки и C необходимо сообщить деформацию всем трем стержням. Таким образом, после сборки нашей статически неопределимой системы в элементах этой системы уже появятся усилия. Определим усилия от неточности изготовления 3-го стержня. Схема решения поставленной задачи не отличается от рассмотренной нами выше.

Прежде всего, выясним число неизвестных. Их будет три . Знак «» указывает на то, что это усилия от неточности изготовления.

Запишем уравнения равновесия:

(1)

Т.е. для трёх неизвестных мы имеем только 2 уравнения равновесия. Отсюда видно, что наша задача является один раз статически неопределимой. Составим одно уравнение совместности деформации. Пусть точки и C нам удалось совместить в некоторой точке . Вследствие чего стержни получат упругие деформации:

(2)

(3)

Из геометрических соображений следует

. (4)

Т.к. то можно записать

; (5)

Тогда на основании (5): . (6)

Преобразуем уравнение совместности деформаций (6)

;

;

. (7)

В (7) подставим (3)

;

.

Поскольку мы считаем, что стержни изготовлены из одного материала

, пусть также

. (8)

Уравнения (1) и (8) составляют замкнутую систему уравнений.

(9)

Со знаками усилий дело обстоит следующим образом. На схеме мы предполагаем усилия положительными. В результате мы получим действительные знаки усилий. Причём, величина берется по абсолютной величине.

Пусть, как и раньше

Тогда монтажные усилия примут значения:

(10)

Мы видим, что монтажные усилия в стержнях зависят от площади поперечного сечения, т.е. фактически от жесткости.

Учет изменения температуры в статически неопределимых системах.

Как уже отмечалось, статически неопределимые системы характерны ещё и тем, что в них помимо монтажных усилий возникают усилия от изменения температуры. Из элементарного курса физики известно, что при изменении температуры изменяются размеры твердых тел – температурная деформация. В статически определимых системах температурная деформация не вызывает упругой деформации стержня. В статически неопределимых системах температурная деформация сопровождается упругими деформациями стержней. Таким образом, в статически неопределимых системах возникают ещё и температурные усилия. Способ определения их в общем-то не отличается от рассмотренных ранее случаев.

Рассмотрим пример определения температурных усилий.

Пусть на нашу статически неопределимую систему не действует никаких внешних нагрузок. Кроме того, представим, что никаких неточностей изготовления нет. После монтажа системы изменилась температура на величину (повысилась) в третьем стержне. Стремясь увеличить свою длину, стержень 3 будет сообщать остальным стержням упругую деформацию, а они в свою очередь будут действовать на стержень 3. Составим уравнение равновесия

(11)

Далее рассмотрим деформацию системы. Пусть в шарнире С стержень 3 не связан с балкой. Тогда стержень получит температурную деформацию, где коэффициент температурного расширения. Но реально два других стержня не позволяют стержню 3 получить эту деформацию полностью. В результате абсолютно жесткая балка займет положение .

. (12)

.

.

Таким образом

. (13)

Преобразуем полученное соотношение совместности деформаций (13):

(14)

Учтем физические соотношения:

;

. (15)

Решаем совместно уравнения (11) и (15):

Пусть

Как видно третий стержень находится в сжатом состоянии, а первый и второй в растянутом.

Учет всех факторов при расчете статически неопределимых конструкций.

В элементах статически неопределимых конструкций возникают усилия и напряжения от внешних сил, от возможных неточностей изготовления стержней (имеется в виду только отклонение по длине) и возможного диапазона изменения температуры. Можно поступать двояко. Во-первых, учесть все факторы сразу, но при составлении уравнений совместности деформаций сложно предугадать знак суммарной упругой деформации. И нужен определенный опыт и навык.

Проще воспользоваться принципом суперпозиции. Мы всегда исходим из того что, появляющаяся деформация в стержнях является только упругой. А она величина аддитивная. В каждом стержне общая деформация равна сумме деформаций от каждого фактора в отдельности (от внешних сил, монтажная и температурная). А поскольку упругая деформация пропорциональна действующей внутренней продольной силе, то внутренняя продольная также представляет сумму сил от каждого фактора в отдельности.

для каждого i-го стержня.

Каждая составляющая суммы определяется отдельно. То есть определяются усилия в стержнях только от внешних сил (), полагая что все элементы изготовлены по проекту и температура не изменяется. Затем определяются монтажные усилия () в предположении отсутствия внешних сил и постоянства температуры. Точно так же определяются температурные усилия (). В рассмотренных выше примерах мы так и поступили.

Рассмотрим пример определения необходимой площади сечений элементов конструкции. По частям эта задача уже была решена выше. Принимаем следующие исходные данные: материал сталь3 (; ; ) ; ; ; ; для стержня 3 .

Решение можно начать с записи условий прочности стержневых элементов конструкции:

Неравенства модульные, так как изначально не ясен знак напряжения. Усилия в стержнях от действия всех факторов уже определены:

Распишем модульные неравенства как двойные и подставим в них усилия:

Каждое двойное неравенство дает два решения для площади положительное и отрицательное значение. Выпишем те, которые дают положительные значения площади

Разрешая неравенства, получаем

Решением системы является .