Главные моменты инерции. Главные оси инерции.

Формулы (18) показывают зависимость моментов инерции от угла поворота осей координат. Если, например, ось совершит полный оборот, то получим бесконечное множество осей, проходящих через одну точку. Следовательно, можно говорить о бесконечном множестве осевых моментов инерции. А в любом множестве имеются экстремальные элементы. То есть при некоторых значениях угла величины осевых моментов инерции будут достигать своих экстремальных значений (максимум и минимум). Экстремальные значения (или максимальные и минимальные) осевых моментов инерции сечения называются главными моментами инерции. Следовательно, оси, относительно которых осевые моменты инерции принимают максимальное и минимальное значения, называются главными осями инерции.

Из формулы (19) следует, что если относительно одной оси осевой момент инерции принимает максимальное значение, то относительно другой перпендикулярной оси, осевой момент инерции минимален.

Если начало координат лежит в центре тяжести сечения, то оси называются центральными осями. Центральных осей можно провести бесконечное множество. Из всего этого множества центральных осей можно выделить оси, относительно которых, осевые моменты принимают экстремальные значения. Такие оси называются главными центральными осями. Осевые моменты инерции относительно главных центральных осей называются главными центральными моментами инерции.

В целях определения главных моментов инерции (т.е.и ), а также положения главных осей инерции решаем задачу экстремума

. (20)

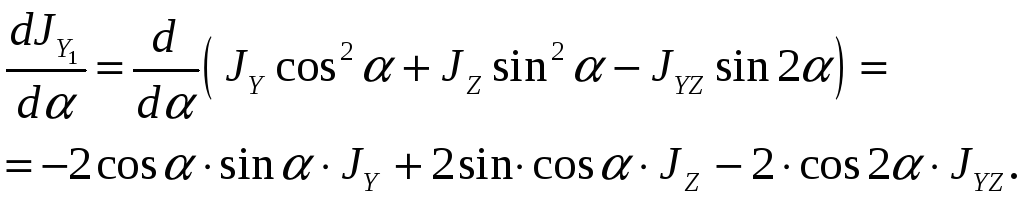
Приравнивая к нулю, получаем

, (21)

где - угол, на который нужно повернуть систему координат, чтобы она стала главной.

Из формулы (21) видно, что

(22)

Таким образом, относительно главных осей инерции центробежный момент инерции равен нулю. Взаимно перпендикулярные оси, из которых хотя бы одна совпадает с осью симметрии сечения, всегда являются главными осями инерции.

Разрешая уравнение (21) относительно угла получим:

. (23)

Угол положительный, когда главная ось повернута относительно исходной оси на угол против часовой стрелки.

Чтобы найти главные центральные моменты инерции нужно в первые две формулы (18) подставить :

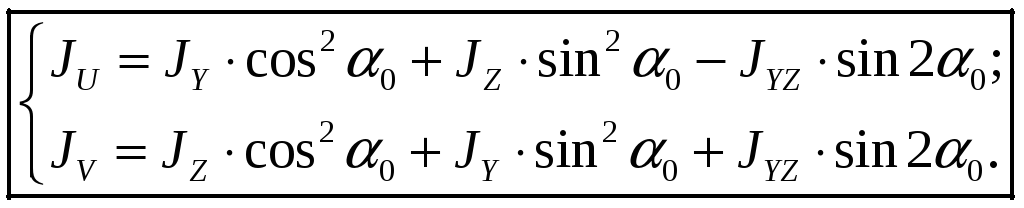(24)

– главные оси инерции.

Можно дать другое выражение для определения экстремальных значений осевых моментов инерции.

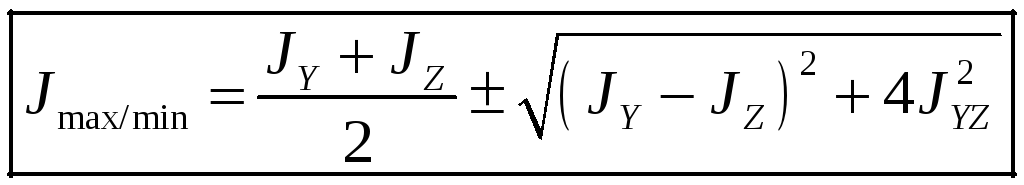(25)

Если известны главные центральные моменты инерции, то моменты инерции относительно осей, повернутых на некоторый угол , выражаются:

(26)

Эллипс инерции

Введем понятие еще об одной геометрической характеристике сечения, связывающей осевой момент инерции с площадью

и (27)

Величины и называются радиусом инерции

; . (28)

Если и главные моменты инерции, то и - главные радиусы инерции.

Эллипс, построенный на главных радиусах инерции, как на полуосях, называется эллипсом инерции. Эллипс инерции имеет уравнение:

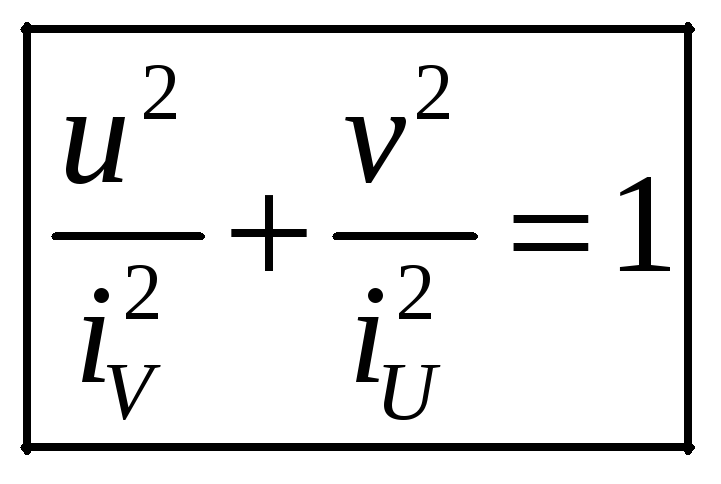. (29)

С помощью эллипса инерции можно графически определить момент инерции относительно любой оси повернутой по отношению к главным осям, например .

Пример определения положения главных центральных осей и главных моментов инерции составного сечения.

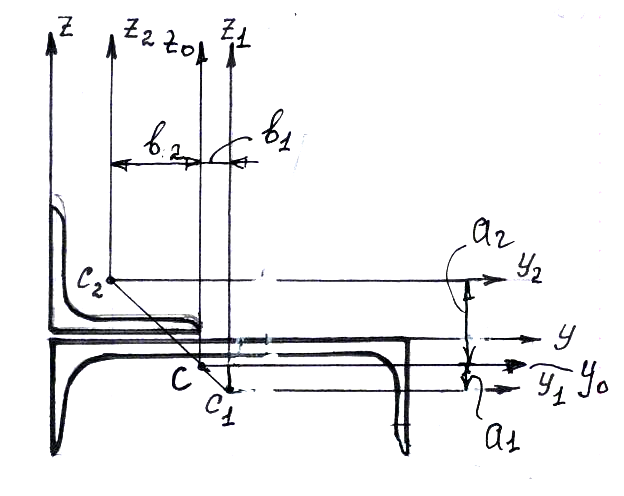
Имеется брус составного сечения: швеллер №20 и уголок . Это стандартные прокатные профили и информацию об их геометрических характеристиках нужно брать из таблицы сортамента согласно тому или иному ГОСТу.

h = 20 cм

b =7.6 cм

A= 23,4cм²

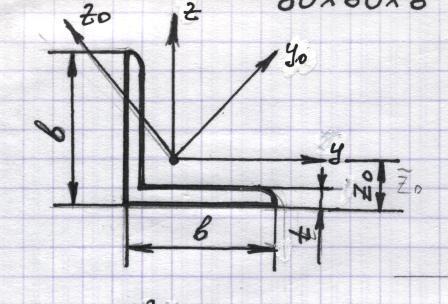
b = 8 cм

t =0.8 cм

A= 12,3cм²

Вначале определяем положение центра тяжести сечения. Для этого вводится система координат , в которой проще всего установить координаты центров тяжести составных частей. При этом используется информация, взятая из таблицы сортамента.

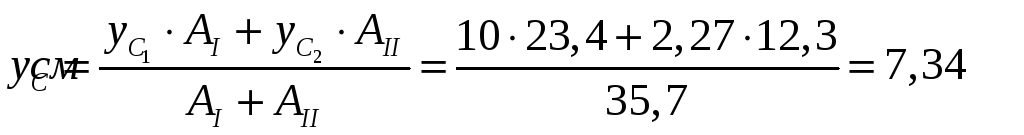
Вводим центральные оси сечения и определяем относительно них моменты инерции сечения. Нужно выбирать исходные центральные оси так, чтобы они были параллельными центральным осям составных частей сечения (в нашем случае швеллер и уголок), относительно которых моменты инерции либо известны (как в данном случае), либо легко определяются. В этом случае используются формулы параллельного перехода (13) и, конечно, свойство аддитивности.

Но вначале определим расстояния между общими центральными осями и центральными осями составных частей. Это производится в системе координат . Причем нужно из координат общего центра тяжести вычитать координаты центров тяжести составных частей либо наоборот. Но нельзя смешивать эти два правила. Иначе может произойти потеря знака у расстояний и это отразится на центробежном моменте и последующих результатах.

Применяя (13) получаем:

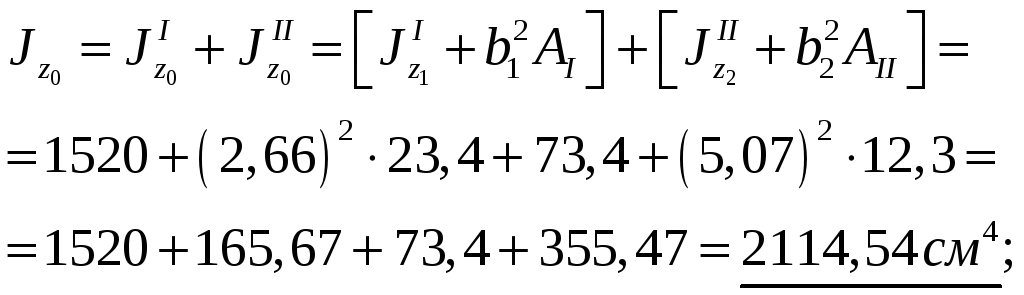
В последнем соотношении вначале нужно было вычислить центробежный момент для уголка, который не задается в таблице сортамента. Нужно воспользоваться третьей формулой (26), полагая (на рисунке для уголка оси являются главными для него)

.

Далее устанавливаем положение главных центральных осей сечения, то есть угол, на который нужно повернуть оси , чтобы они заняли положение главных осей. Используя (23) получаем:

То есть исходные центральные оси нужно повернуть на по часовой стрелке, чтобы они заняли положение главных центральных осей. Для определения главных моментов инерции воспользуемся (25)

Откуда находим

.

Целесообразно произвести проверку:

;

2171,92+280,92 =2453,37;

2114,54+338,83=2452,84.

С учетом ошибок округления при вычислениях это практически совпадение.

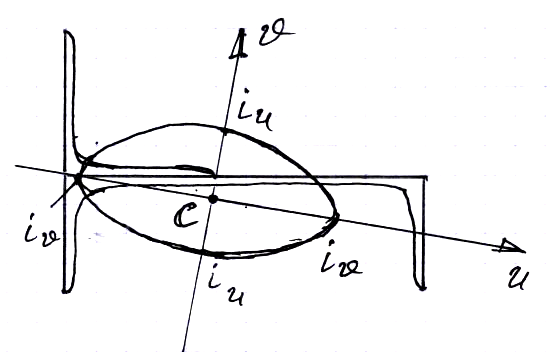Осталось ввести главные центральные оси рассматриваемого сечения, обозначив их, например, . Далее следует установить соответствие между введенными главными осями и вычисленными ранее главными моментами инерции (). Принцип достаточно простой. Поскольку , то главная ось максимального момента инерции будет располагаться около оси , и тогда

;

.

Вычисляем главные радиусы инерции сечения

И на главных осях строим в масштабе сечения эллипс инерции согласно уравнению (29).

В заключении к теме отметим некоторые важные моменты. В дальнейшем под геометрией поперечных сечений должны подразумеваться, во-первых, главные центральные оси и, во-вторых, помимо площади нужно определять моменты инерции относительно этих осей. Главные центральные оси это своего рода аналоги геометрическим осям симметрии сечений, если геометрическая симметрия отсутствует. Симметрия в смысле проявления прочностных и жесткостных свойств бруса при нагружении его внешними поперечными силами (т. е. изгибе).

Если брус имеет постоянное сечение с неизменной ориентацией по всей длине, то вводится понятие главных плоскостей бруса. Главная плоскость содержит продольную ось и одну из главных центральных осей всех поперечных сечений. Таким образом, у бруса постоянного сечения имеются две взаимно перпендикулярные главные плоскости (геометрическая плоскость симметрии автоматически главная).

Главные плоскости (как и плоскости симметрии) имеют важную особенность. При нагружении бруса внешними поперечными силами в главной плоскости происходит изгиб в той же плоскости (плоский изгиб). При изгибе в одной главной плоскости брус (балка) проявляет максимальные прочностные и жесткостные свойства, а при нагружении в другой главной плоскости, наоборот, самые минимальные прочностные и жесткостные свойства. Достаточно взять обычную ученическую линейку, чтобы убедиться в сказанном.

Эллипс инерции (если он построен) как раз указывает не только положение главных плоскостей бруса (как и положение главных центральных осей симметрии сечения), но и на то какая плоскость имеет наивысшую прочность и жесткость, и какая плоскость наиболее слабая у бруса данного поперечного сечения.

Лекция № 12