Лекция 3

ИЗГИБ БАЛОК. ДИФФЕРЕНЦИАНАЛЬНЫЕ ЗАВИСИМОСТИ ПРИ ИЗГИБЕ БАЛОК

I. Понятие о деформации изгиба.

При центральном растяжении или сжатии, а также при кручении прямых брусьев, их оси, первоначально прямые, остаются прямыми и при деформации. В отличие от этих типов деформации изгиб представляет собой такую деформацию, при которой происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев. При изгибе брусьев часть волокон параллельных оси бруса укорачивается, а другая часть волокон удлиняется. Поверхность, разделяющая эти части называется нейтральным слоем и характеризуется тем, что, не изменяя длины, изгибается.

Изгиб связан с возникновением в поперечных сечениях бруса изгибающих моментов. Изгибающий момент является одним из внутренних силовых факторов.

Пусть внешние силы лежат в плоскости, которая содержит продольную ось бруса. Кроме того, силы действуют в направлении перпендикулярном оси бруса. Причем плоскость П проходит через Х и Z. Тогда внешние силы в каждом поперечном сечении вызовут изгибающий момент относительно оси Y , лежащей в поперечном сечении и проходящей через центр тяжести.

Момент относительно оси Y работает в плоскости XOZ, которая является перпендикулярной поперечному сечению. Кроме изгибающего момента в поперечном сечении присутствует и поперечная сила .

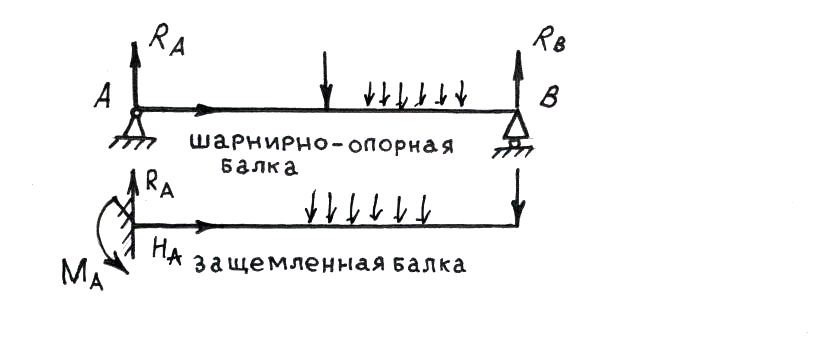
Типы опирания балок

Балки являются часто встречающимися элементами сооружений и машин. Они принимают давление от одних элементов конструкции и передают их тем частям, которые поддерживают балки. Кроме активных внешних сил необходимо знать и реактивные силы (реакции опор). Но прежде чем вычислить реакции опор необходимо представлять устройство опор для балок. Существуют три типа опор:

а) шарнирно-неподвижная опора;

б) шарнирно-подвижная опора;

в) защемление.

Шарнирно-неподвижная опора схематично изображена на рисунке в точке А. Она позволяет опорному сечению балки свободно поворачиваться вокруг шарнира. Однако этот тип опоры не допускает поступательного перемещения опорного сечения балки. Сопротивление поступательному перемещению выражается реакцией, которая передается от опоры через шарнир на балку. Реакция лежит в плоскости действия внешних сил. В случае шарнирно-неподвижной опоры известны только точка приложения реакции, но не известны ни величина реакции, ни её направление. Обычно реакция R раскладывается на составляющие и . Таким образом шарнирно-неподвижная реакция дает две неизвестные по величине реакции.

Шарнирно-подвижная опора помимо поворота вокруг шарнира допускает также свободное поступательное перемещение в одном из направлений. Такая опора препятствует лишь перемещению в направлении перпендикулярном направлению незапрещенного перемещения. Шарнирно - подвижная опора дает лишь одну неизвестную реакцию .

При защемлении (заделке) запрещается всякое перемещение соответствующего торца балки в плоскости действия внешних сил. Заделка может быть получена из шарнирно-неподвижной опоры путем уничтожения шарнира. Значит, помимо неизвестных реакций и в заделке мы должны ввести ещё одну реакцию, препятствующую повороту. Такой реакцией может быть только пара сил (момент относительно точки А). Балки могут опираться на ряд опор рассмотренных типов.

При определении реакций, в первую очередь, используются уравнения статики (равновесия). Уравнения равновесия выражают ту мысль, что балка в целом при действии всех сил и реакций, должна находиться в равновесии. Так как все силы лежат в одной плоскости, то уравнений равновесия для них может быть записано только три. Поэтому, чтобы вычислить реакции из условий равновесия балка должна опираться на опоры, дающие в сумме три неизвестные реакции. Такие балки называются статически определимыми балками. Все остальные относятся к статически неопределимым балкам.

Примеры статически определимых балок

После выбора расчетной схемы и определения опорных реакций завершается первая часть решения задачи – определение внешних сил действующих на балку. Далее переходим к отысканию внутренних силовых факторов.

Внутренние силовые факторы при изгибе

Рассмотрим сечение 1-1. Выясним силовые факторы, действующие в этом сечении. Чтобы удержать в равновесии рассматриваемую часть, действие отброшенной части заменим силой , действующей в плоскости сечения. Величину этой силы можно определить из условия равновесия рассматриваемой части.

.

Отсюда .

Вдоль оси рассматриваемой части никакие внешние силы не действуют, отсюда внутренняя продольная сила равна нулю. Выполнив указанное условие, мы обеспечим равновесие вдоль и .

Введенная сила не может воспрепятствовать повороту рассматриваемой части. Этот поворот может исключить пара сил. Величина момента в сечении 1-1 определяется из условия равновесия рассматриваемой части (записывается сумма моментов относительно оси Y, проходящей через точку ).

Таким образом, при изгибе балки в поперечном сечении возникает поперечная сила и изгибающий момент .

Поперечная сила Q сдвинет рассматриваемое сечение относительно смежного. Она вычисляется как алгебраическая сумма проекций на ось Z сил, действующих на одну сторону от сечения.

Изгибающий момент поворачивает это сечение относительно смежного. Он равен алгебраической сумме моментов всех внешних сил, расположенных по одну сторону от сечения относительно оси Y, проходящей через т..

Правило знаков для Q и M

При определении поперечной силы и изгибающего момента правило знаков можно формулировать следующим образом. Поперечная сила Q положительна, если внешние силы, действующие на рассматриваемую часть, стараются повернуть её против хода часовой стрелки. Момент является положительным, если внешние силы действуют на рассматриваемую часть так, что волокна с положительной координатой Z растягиваются.

Определим Q и M в сечении . Рассмотрим уравнения равновесия левой части:

Если рассматривать правую часть то:

Дифференциальные зависимости между интенсивностью распределенной

нагрузки, поперечной силой и изгибающим моментом

Для равновесия отсеченной части балки в рассматриваемом сечении следует приложить внутренние силы Q и M, заменяющие действие отброшенной части. Если из балки вырезать элемент бесконечно малой длины , то этот элемент должен находиться в равновесии. На элемент действует часть нагрузки , которую на такой малой длине можно считать постоянной и равной в сечении .

Кроме того, на элемент действуют силы и моменты , заменяющие действие отброшенных частей. Вследствие малости расстояния , можно положить, что

и

Выпишем условия равновесия выделенного элемента:

( 1 )

( 2 )

Или:

отсюда или

( 3 )

производная от поперечной силы по абсциссе (координате) сечения равна интенсивности сплошной нагрузки в том же сечении с обратным знаком. Из уравнения моментов, пренебрегая величиной второго порядка малости по сравнению с другими слагаемыми, имеем

или ( 4 )

Производная от момента по абсциссе сечения равна поперечной силе в том же сечении.

Если взять производную от обеих частей (4) получим:

, учитывая (3) получим:

( 5 )

Полученные зависимости (3), (4), (5) могут быть использованы при построении эпюр Q и M. Здесь большую роль играет тот факт, что производная функции геометрически представляет собой тангенс угла наклона касательной к линии графика и оси абсцисс в данной точке.

Так поперечная сила Q может рассматриваться как тангенс угла наклона касательной к эпюре M, в точке соответствующей этому сечению. Из (3) следует, что поперечная сила принимает экстремальные значения в сечениях, где , т.е. (касательная к эпюре параллельна оси ). Из (4) следует, что в сечениях, где изгибающий момент достигает экстремального значения.

Пример 1.

Определение реакций:

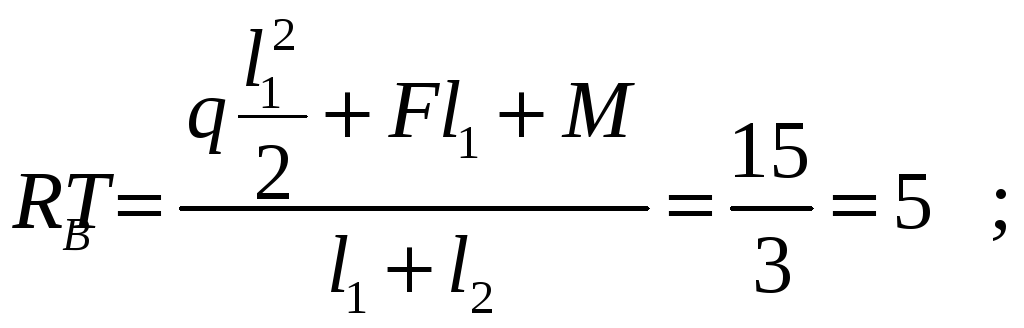
Разбиваем на участки:

Вычислим экстремальное значение момента на I участке. Для этого используется зависимость: Определим сечение, где момент принимает экстремальное значение, т.е.

Поскольку зависимость момента квадратичная нужно определить форму кривой графика функции момента по дифференциальному соотношению .

Вторая производная есть кривизна кривой, если кривизна положительная, то вогнутость вниз.

В нашем случае величина , поскольку направление q не совпадает с направлением Z, тогда на I участке .

II участок:

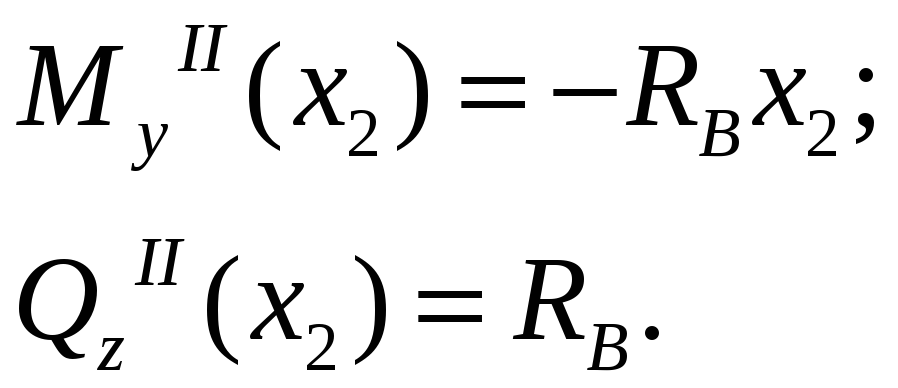
Функции простые, определяем их значения на концах участка: