Лекция 4

ПРИМЕРЫ ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ

СИЛОВЫХ ФАКТОРОВ

Пример 2 (балки)

Дано: q=2 T/м, F=3T, М=5 Т м

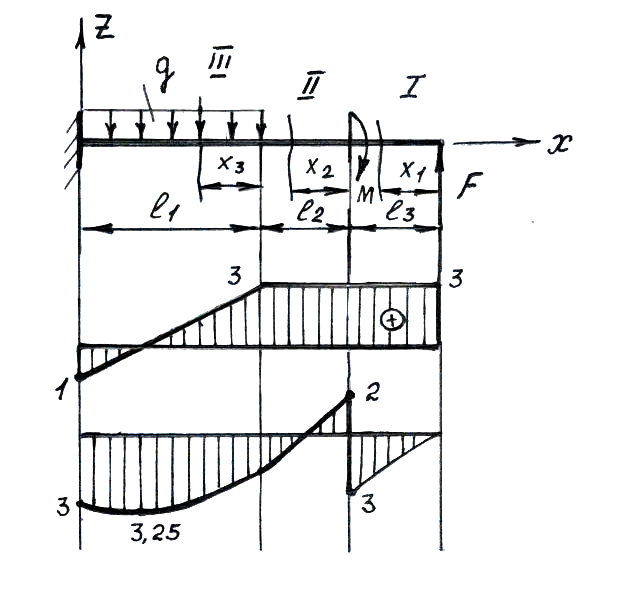
В данном случае реакции опор можно не определять, т.к. с одного торца все силы известны. Разбиваем на участки.

I участок:

;

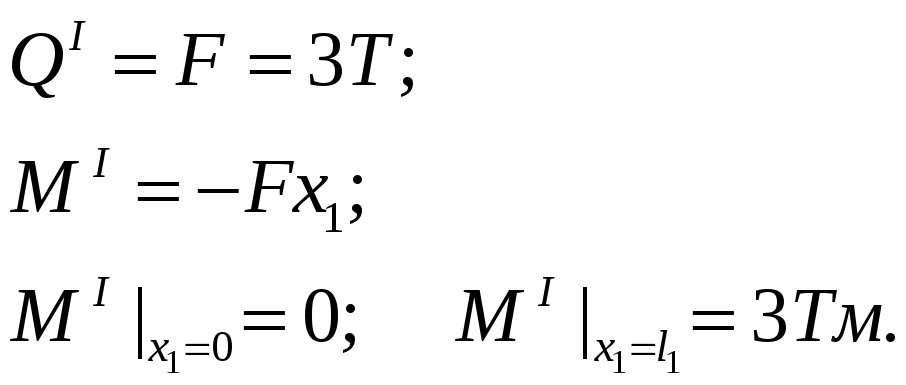
II участок:

;

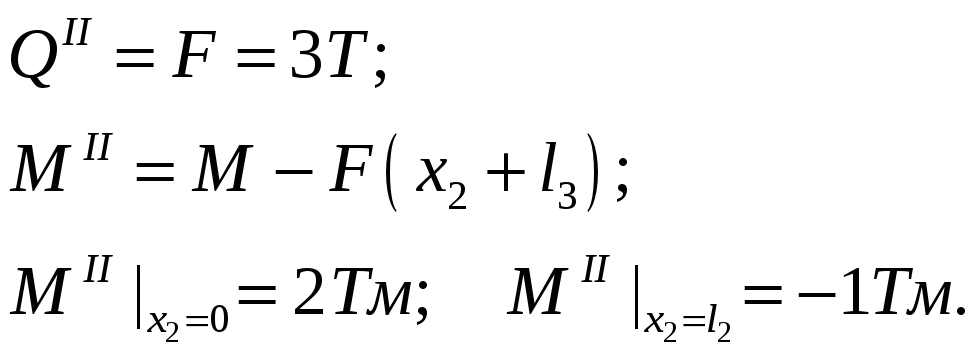
III участок:

;

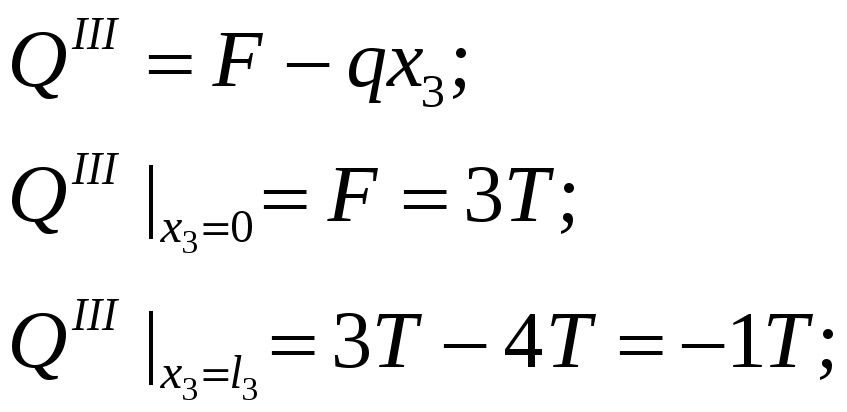
Момент в пределах третьего участка изменяется по квадратичному закону. Чтобы определить экстремальное значение момента на участке, необходимо воспользоваться дифференциальной зависимостью:

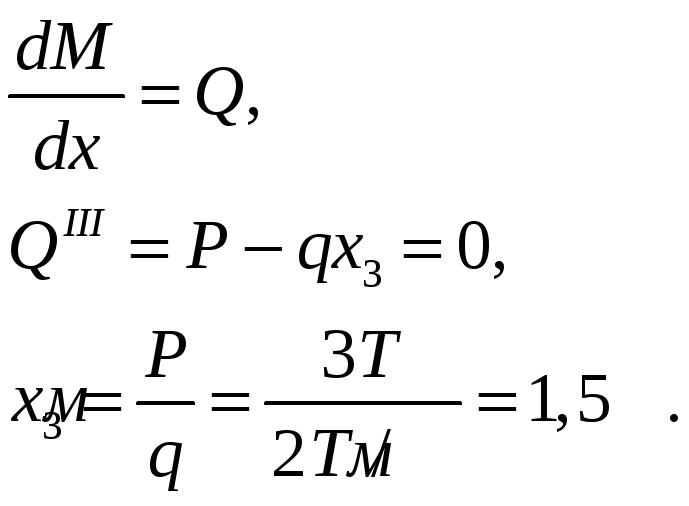
Итак, при момент имеет экстремальное значение.

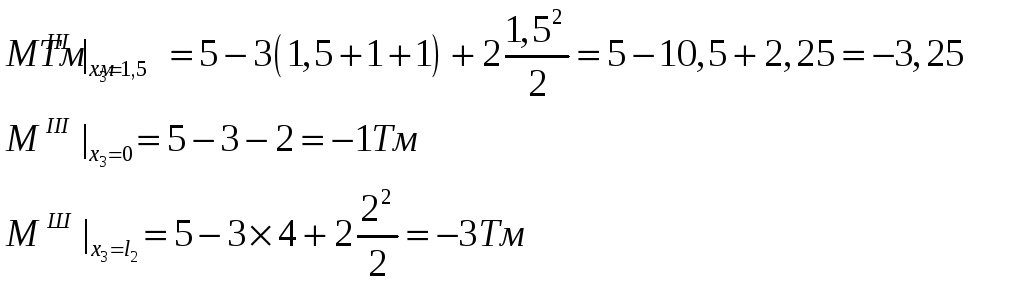
По полученным данным строим эпюры Q и M. Далее проводится анализ правильности построения эпюр, используя дифференциальные зависимости:

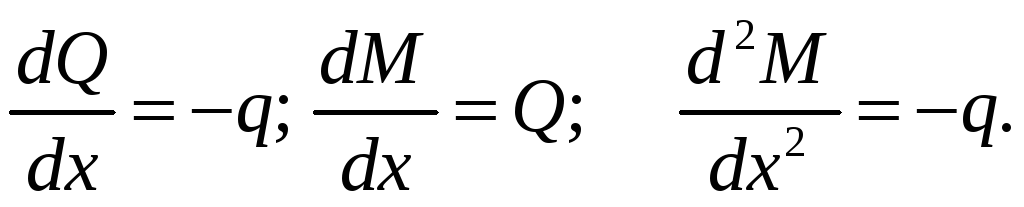
Пример 3 (плоские рамы)

Наряду с прямыми стержнями и прямыми балками на практике имеют применение брусья с ломаной осью. Особенность их заключается в том, что они работают одновременно и как стержни и как балки. То есть в поперечных сечениях возникают продольные силы, поперечные силы и изгибающие моменты. Пока мы остановимся на брусьях, ломаная ось которых лежит в одной плоскости.

Д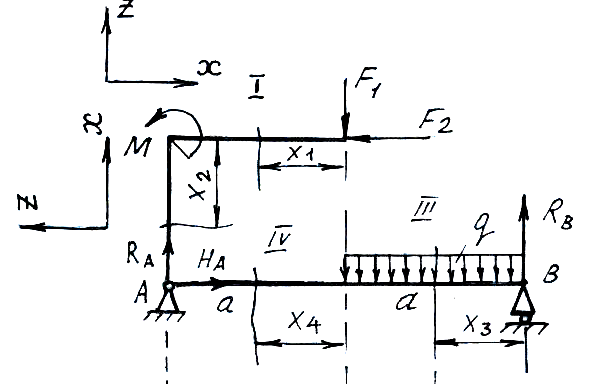ано:

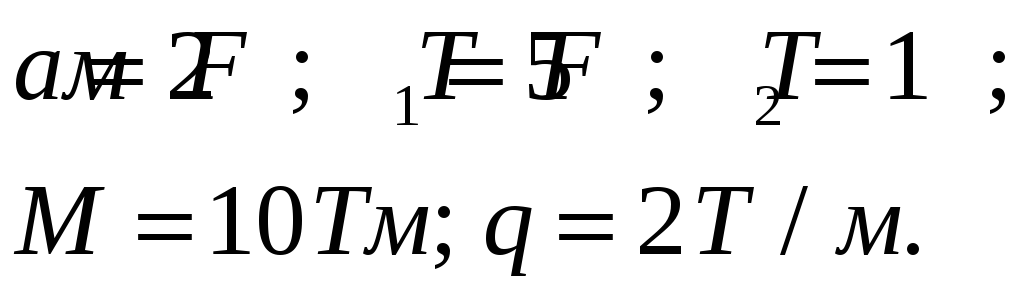
Определим реакции опор. Рама опирается на две опоры (неизвестных -3). Рама является статически определимой.

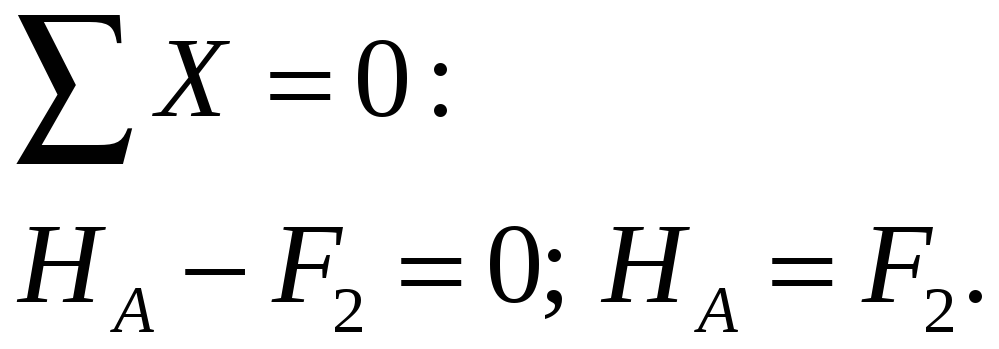
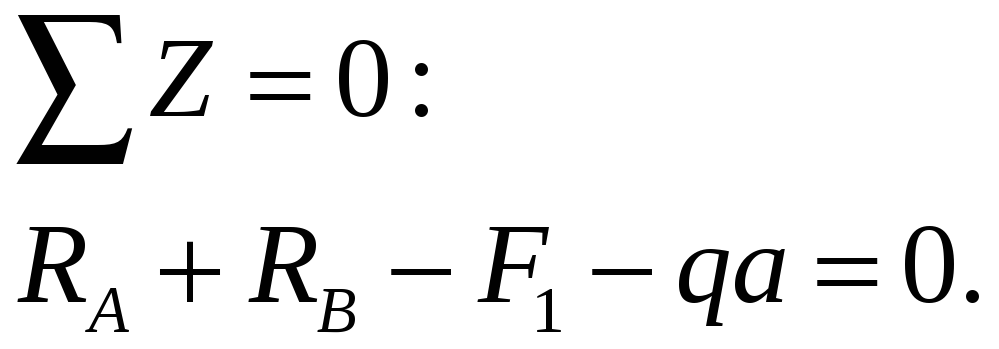
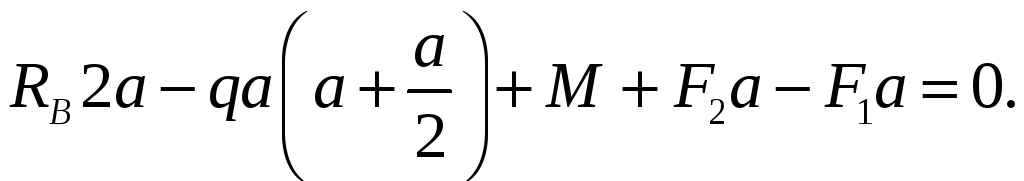
Разбиваем на участки по известному принципу. Далее на каждом из участков берется поперечное сечение и с помощью метода сечения определяются силовые факторы. Кроме того, на каждом из участков нужно ввести систему координат так, чтобы ось была направлена вдоль оси соответствующего участка, а ось перпендикулярно.

I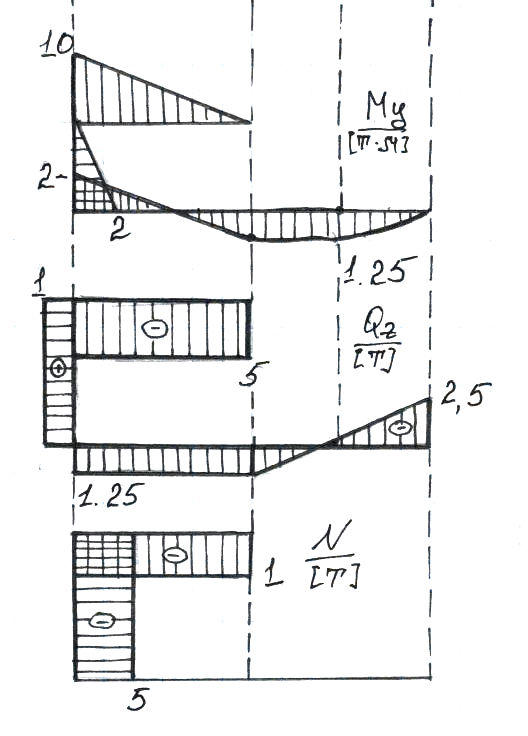 участок:

;

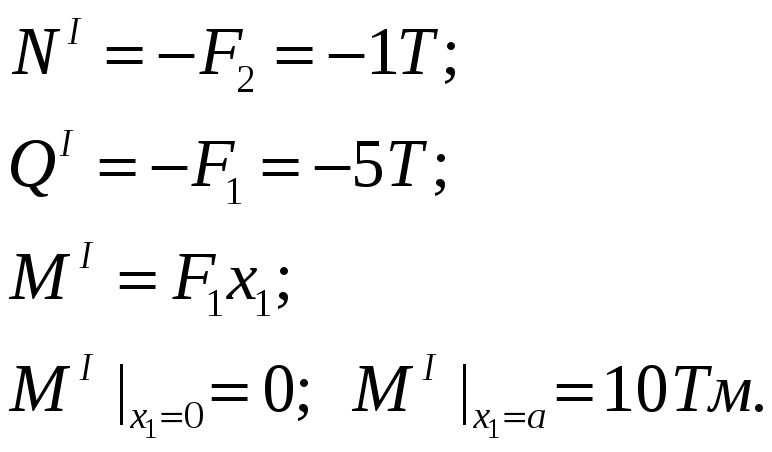
II участок:

;

Ш участок:

;

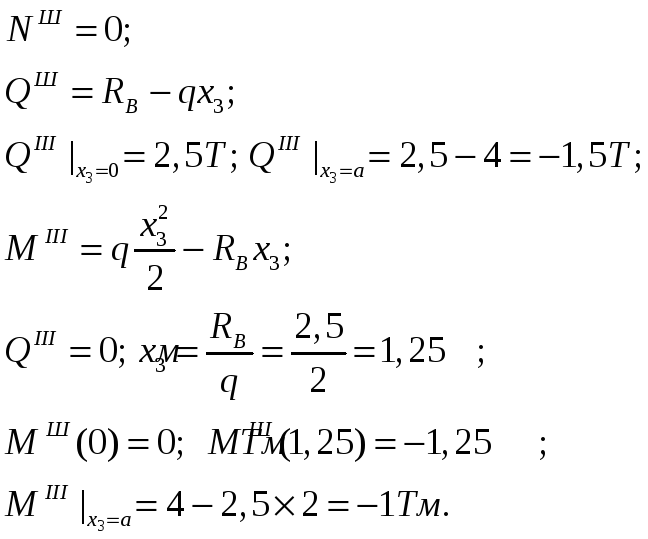
IY участок:

;

Пример 4

Д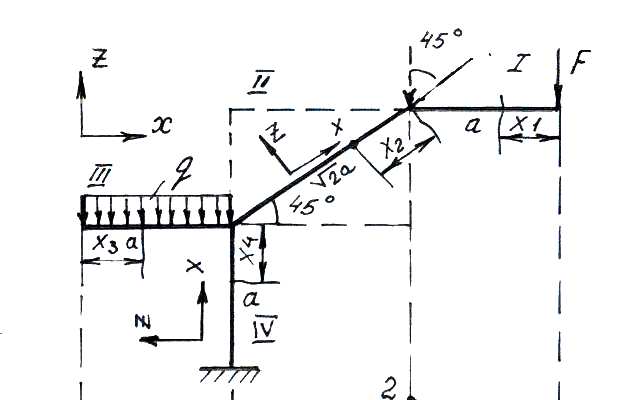ано:

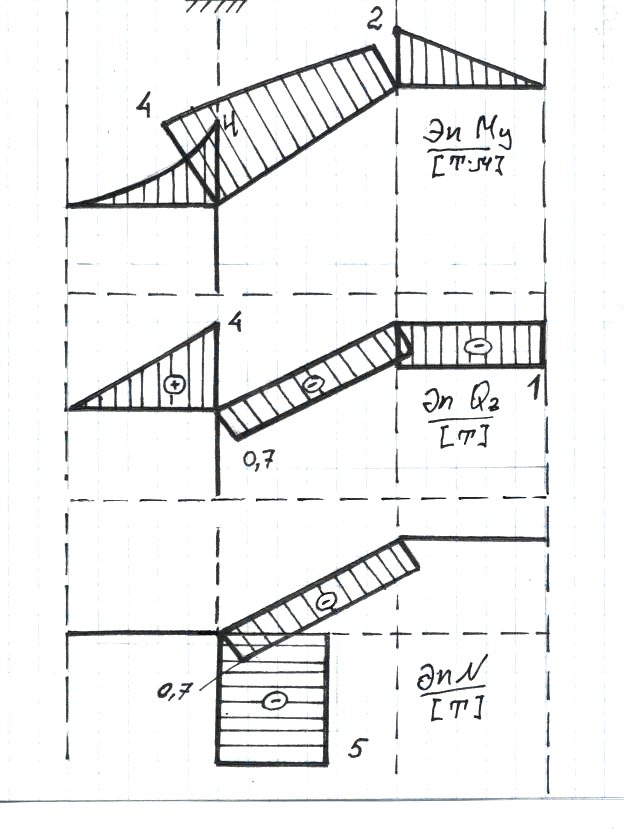
Реакции опор определять нет необходимости. Разбиваем на участки.

I участок:

;

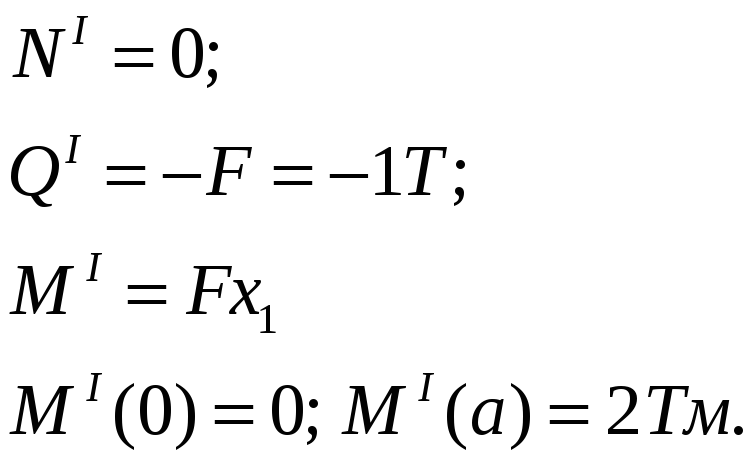
II участок:

;

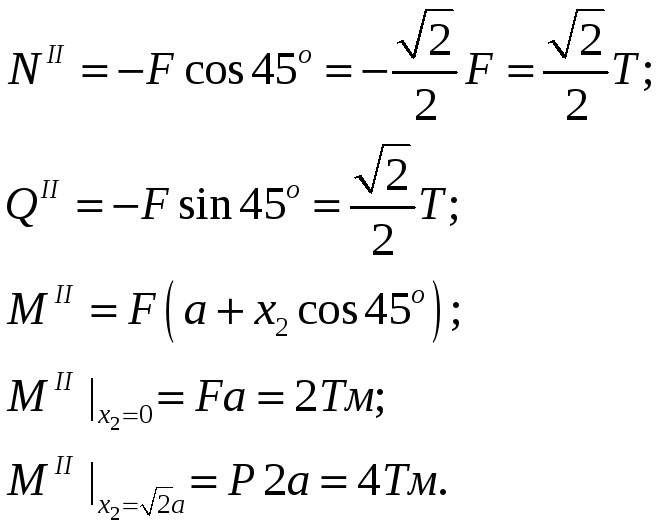
III участок:

;

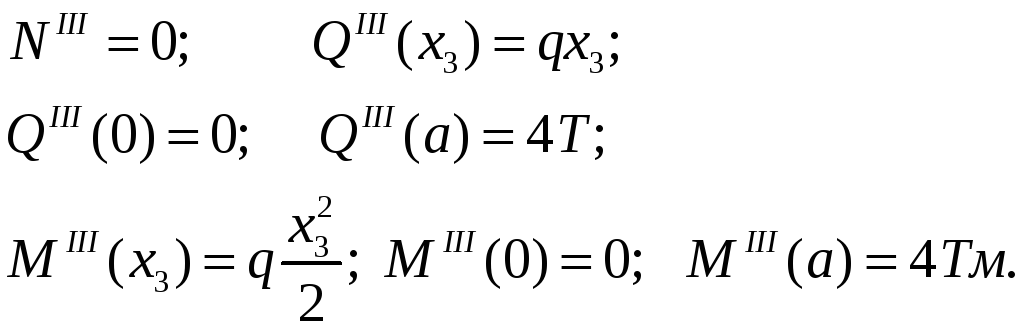
IY участок:

;

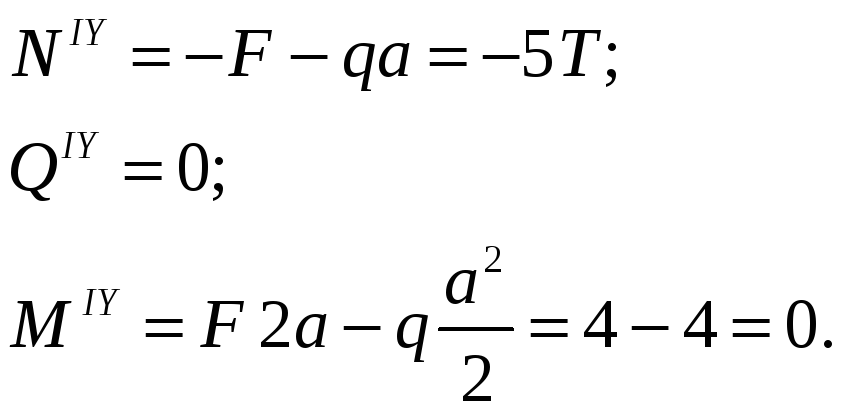
Пример 5. Построение эпюр для бруса с кривой осью. В отличие от плоских рам в кривых брусьях кривизна изменяется непрерывно. Поперечные сечения меняют ориентацию при перемещении вдоль оси. Поэтому меняются от сечения к сечению не только значения внутренних сил и , но их направления. Если рассматриваются брусья с продольной осью в виде части окружности, то положение поперечных сечений проще задавать угловой координатой. В остальном также работает метод сечений.

Дано:

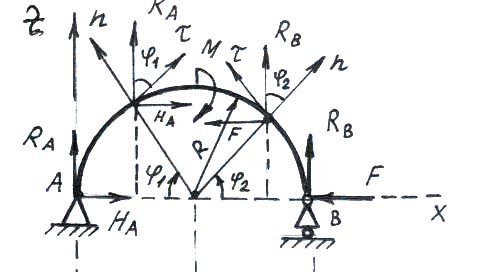Решение начнем с определения реакций опор.

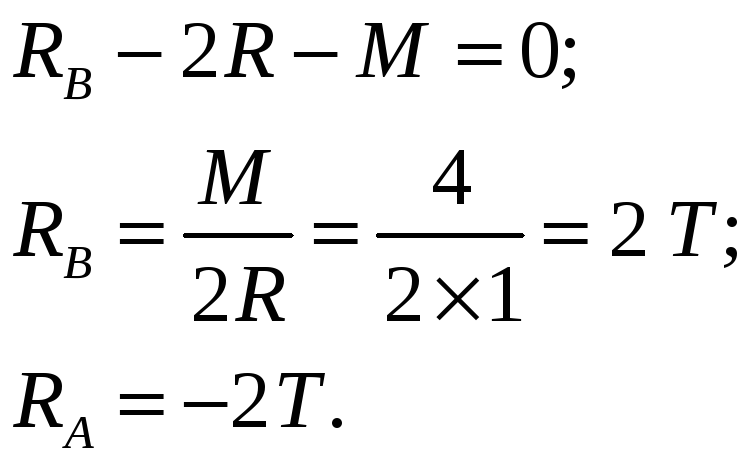
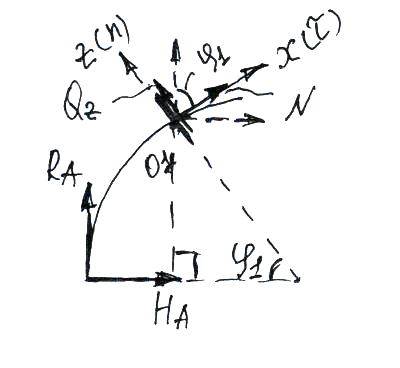
Разбиваем на участки:

I участок: ;

Нужно составить уравнения равновесия рассматриваемой части (левой) в системе координат связанной с данным сечением, так как легче определять проекции сил.

Далее выражаем функции:

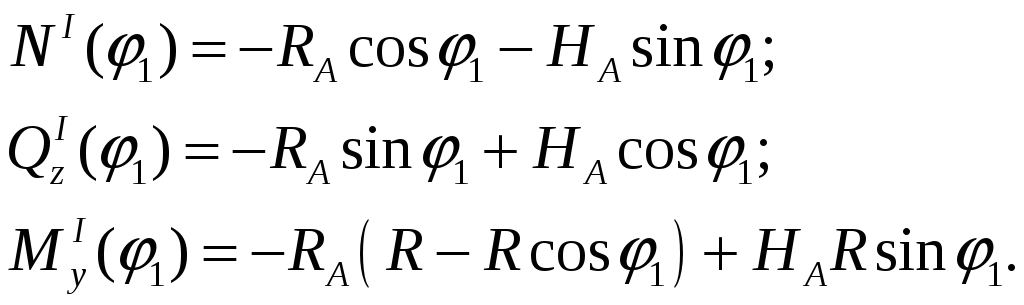
II участок: ;

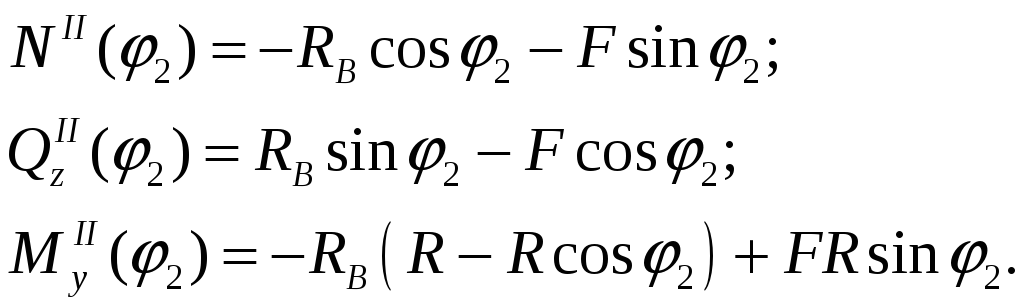
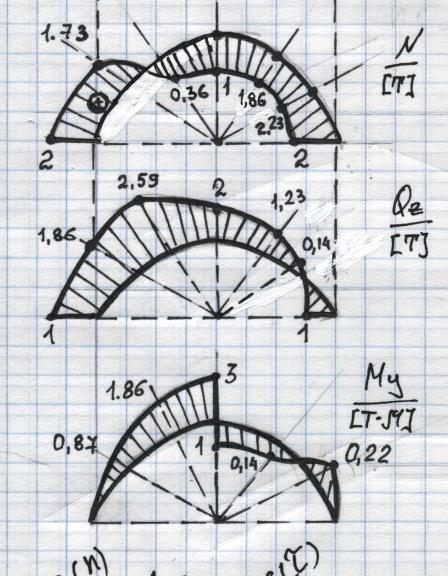
Графики тригонометрических функций строятся по ряду точек. Удобно воспользоваться таблицей, и затем значения перенести на эпюры.

Iучасток II участок

N	2	1,73	-0,36	-1	-1	-1,86	-2,23	-2
Q	1	1,86	2,59	2	2	1,23	0,14	-1
M	0	0,78	1,86	3	-1	-0,14	0,22	0