Int *fun (intx,int *y);

Вызов функции возможен только после инициализации значения указателя fun и имеет вид:

(*fun)(i,&j);

В этом выражении для получения адреса функции, на которую ссылается указатель fun, используется операция разадресации *.

Указатель на функцию может быть передан в качестве параметра функции. При этом разадресация происходит во время вызова функции, на которую ссылается указатель на функцию. Присвоить значение указателю на функцию можно в операторе присваивания, употребив имя функции без списка параметров.

double (*fun1)(int x, int y);

double fun2(int k, int l);

fun1 = fun2; /* инициализация указателя на функцию */

(*fun1)(2,7); /* обращение к функции */

Указатель на функцию fun1 описан как указатель на функцию с двумя параметрами, возвращающую значение типа double, и также описана функция fun2. В противном случае, т.е. когда указателю на функцию присваивается функция, описанная иначе, чем указатель, произойдет ошибка.

Пример 27. Разработать функцию, вычисляющую производную от функции cos(x) с использованием указателя на функцию в качестве параметра.

double proiz(double x, double dx, double (*f)(double x) );

double fun(double z);

Int main()

{

double x; /* точка вычисления производной */

double dx; /* приращение */

double z; /* значение производной */

scanf("%f,%f",&x,&dx); /* ввод значений x и dx */

z=proiz(x,dx,fun); /* вызов функции */

printf("%f",z); /* печать значения производной */

return 0;

}

double proiz(double x,double dx, double (*f)(double z) )

{ /* функция вычисляющая производную */

double xk,xk1,pr;

xk=fun(x);

xk1=fun(x+dx);

pr=(xk1/xk-1e0)*xk/dx;

return pr;

}

double fun( double z)

{ /* функция от которой вычисляется производная */

return (cos(z));

}

Для вычисления производной от какой-либо другой функции можно изменить тело функции fun или использовать при вызове функции proiz имя другой функции. В частности, для вычисления производной от функции cos(x) можно вызвать функцию proiz в форме

z=proiz(x,dx,cos);

а для вычисления производной от функции sin(x) в форме

z=proiz(x,dx,sin);

Рекурсивные функции

Под рекурсивным определением подпрограммы или под рекурсией будем понимать такое описание (представление) подпрограммы, которое содержит внутри себя ссылку на определяемую подпрограмму. Другими словами, подпрограмма из своего тела осуществляет вызов непосредственно самой себя (прямая рекурсия) с другими аргументами (параметрами), либо вызывает саму себя из других подпрограмм (функций или процедур), находящихся внутри тела рекурсивной подпрограммы (косвенная рекурсия). Далее, говоря о рекурсивных функциях или процедурах, будем подразумевать, что все сказанное относится и к тем и к другим, т.е. в общем случае – к подпрограммам.

Определение рекурсивных объектов в математике происходит по индукции. При этом сначала формулируется базис индукции, как рекурсивное определение исключительных случаев при вычислении функции, а затем шаг индукции, как рекурсивное правило построения того же объекта. Под индукцией понимается метод доказательства утверждений, который строится на базе индукции при n = 0, 1, затем утверждение полагается правильным при n=n, и проводится доказательство для n+1.

Часто используется термин рекуррентные соотношения, который определяет математическое задание функции с помощью рекурсии. Основной задачей исследования рекурсивно заданных функций является получение f(n) в явной или как еще говорят «замкнутой» форме, т.е. в виде аналитически заданной функции, выражающейся через саму себя.

Важнейшим признаком любой рекурсивной функции является условие выхода из рекурсии. Такое условие выхода содержится, как правило, в самом начале рекурсивных функций и определяет, когда рекурсия должна быть закончена и применен базис индукции.

Рекурсивные функции очень часто используются в программировании, так как многие математические задачи носят рекурсивный характер. Решение задач с помощью рекурсивных функций бывает более изящным и коротким, чем не рекурсивное решение. Тем не менее, любая рекурсивная процедура или функция имеет аналог без использования рекурсии, с помощью последовательных итераций (тезис Черча-Тьюринга). Изучению и исследованию рекурсивных функций посвящены целые разделы современной математики – теория вычислений, теория вычислимости, теория алгоритмов, теория рекурсивных функций. Практика показывает, что использовать в программировании рекурсивные процедуры и функции необходимо осторожно, поскольку непонимание механизмов рекурсии может привести к бесконечным циклам, зависанию программы, большим затратам времени выполнения и используемой памяти.

Пусть Р – рекурсивная подпрограмма, тогда выполнение действий в рекурсивной подпрограмме может быть организовано одним из следующих способов (рис.33):

int P(); { P; операторы; }	int P(); { операторы; P; }	int P(); { операторы; P; операторы; }
Рекурсивный подъём	Рекурсивный спуск	Рекурсивный спуск и рекурсивный подъём

Рис.33. Способы вызова рекурсивных подпрограмм

Пример 28. Представим в виде рекурсии функцию вычисления суммы двух натуральных чисел.

Сначала проанализируем задачу.

Пусть X=23 – это первое число, второе число Y=34. Сумма их равна:

F₁ = Sum (X, Y) = X+Y = Sum (23, 34)= 23+34=57

Уменьшим X на 1 и опять найдем сумму, X=23–1=22. Тогда

F₂ = Sum (X–1,Y) = X–1+Y = Sum (22,34)= 22+34=56=F₁ – 1

Видим, что при уменьшении первого слагаемого на 1, сумма тоже уменьшилась на 1. Последнее можно выразить так:

F₂ = Sum (X–1,Y) = (X–1) + Y = (X+Y) – 1= Sum (X,Y)–1.

Т.е. получили рекуррентное соотношение: Sum (X–1,Y) = Sum (X,Y)–1, отсюда:

Sum (X,Y) = Sum (X–1,Y)+1.

Т.е. для вычисления суммы некоторого числа X с числом Y нужно вычислить сумму предыдущего числа X – 1 c Y и прибавить к ней 1.

Теперь нужно определить граничные условия или условие завершения рекурсии (базис индукции). Мы видим, что на каждом шаге X уменьшается на 1. До какой границы это нужно делать? Очевидно, пока Х не станет равным 0, т.к. по условию – числа натуральные. Но сумма любого числа с нулем дает в результате это число, т.е. граничное условие будет таким Sum(0,Y) = Y.

Итак, окончательная рекуррентная формула для сложения двух натуральных чисел такая:

Для такой формулы просто написать рекурсивную функцию:

int SumXY (int x, int y)

{

if (x == 0) return(y);

else return(SumXY(x-1,y)+1);

}

Аналогично можно вывести рекуррентные соотношения для операций целочисленного (натурального) вычитания, умножения, деления, вычисления остатка от деления:

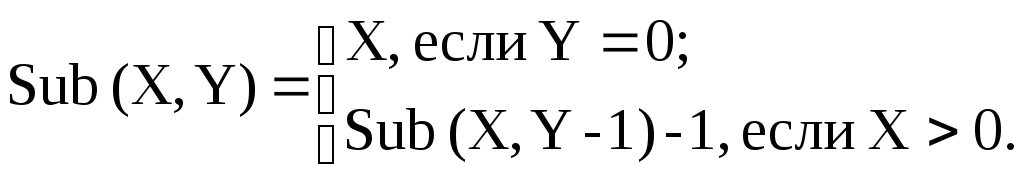
Пример 29. Напишем программу для реализации этих рекурсивных функций:

int SumXY (int x, int y)

{

if (x == 0) return(y);

else return(SumXY(x-1,y)+1);

}

int SubXY (int x, int y)

{

if (y == 0) return(x);

else return(SubXY(x,y-1)-1);

}

int MultXY (int x, int y)

{

if (y == 1) return(x);

else return(MultXY(x,y-1)+x);

}

int DivXY (int x, int y)

{

if (x <= y) return(0);

else return(DivXY(x-y,y)+1);

}

int MODXY (int x, int y)

{

if (x < y) return(x);

else

if (x == y) return(0);

else return(MODXY(x-y,y));

}

int main()

{

int a,b;

printf("Введите целое положительное A:\n");

scanf("%i",&a);

printf("Введите целое положительное B:\n");

scanf("%i",&b);

printf(" A + B = %d" , SumXY(a,b));

printf(" A - B = %d" , SubXY(a,b));

printf(" A * B = %d" , MultXY(a,b));

printf(" A / B = %d" , DivXY(a,b));

printf(" A mod B = %d" , MODXY(a,b));

}

Пример 30. Напишем программу для реализации алгоритма Евклида нахождения наибольшего общего делителя (НОД) двух натуральных чисел. Данный алгоритм был впервые описан в книге Евклида "Начала" (около 300 г. до н.э.). Суть алгоритма в следующем: пусть m и n одновременно неравные 0 целые неотрицательные числа и пусть m>n. Тогда если n=0, то НОД(m,n)=m; если же n≠0, то для чисел m, n, r (где r – остаток от деления m на n) выполняется равенство НОД(m,n)=НОД(n,r).

Из описания алгоритма выводим рекуррентное соотношение:

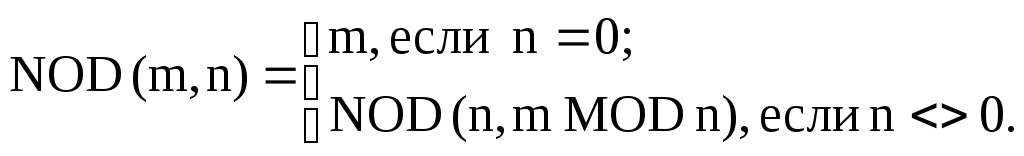
Кроме того, вычислим на основе НОД наименьшее общее кратное (НОК), вспомнив формулу связи между НОД и НОК: .

Напишем также функцию, которая вычисляет НОД без рекурсии. Для этого заметим, что мы можем использовать цикл, постоянно вычисляя остаток от деления до тех пор, пока он не станет равным 0.

Алгоритм будет такой: