2.5. Спектральная плотность

Спектральная плотность случайного процесса (называемая также автоспектром) описывает общую частотную структуру процесса через спектральную плотность среднего значения квадрата его значений. Среднее значение квадрата значений реализации в интервале частот от  до  + можно получить, подавая эту реализацию на вход полосового фильтра с узкой полосой пропускания и осредняя возведенную в квадрат функцию на выходе фильтра. Это осредненное значение квадрата приближается к точ­ному его значению при стремлении Т к бесконечности:

Здесь x(t, f,) - составляющие функции x(t), имеющие частоты в интервале от f до +. При малых  спектральную плотность G_x(f) можно определить, пользуясь приближенным равенством:

Более строго:

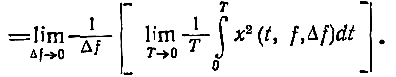
Величина G_x(f) - всегда действительная, неотрицательная функция.

2.6. Теоремы о дискретном представлении случайных процессов

Реализации случайного процесса с непрерывным временем часто представляются и анализируются в дискретной форме. Здесь приведены две важные теоремы о дискретном представлении случайных процессов, необходимые для понимания излагаемого далее материала.

Пусть реализация x(t) случайного процесса {x(t)} задана в интервале времени от 0 до Т секунд и равна нулю вне этого интервала. Преобразование Фурье этой реализации выглядит следующим образом:

(2)

Для того чтобы получить периодическую функцию с периодом Т секунд, предположим, что реализация x(t) непрерывно повторяется.

Основное приращение частоты =1/Т. Разлагая функцию в ряд Фурье, находим:

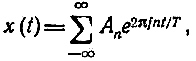
Из формулы (2) следует, что:

(3)

Таким образом, величина Х(п/Т) определяет значения коэффициентов А_п и, следовательно, ординаты x(t) при всех t. Вид функции x(t) в свою очередь определяет величины X(f) при всех значениях f. Этот вывод составляет содержание теоремы о дискретном представлении процесса в частотной области. Основное приращение частоты f = 1/Т называется коинтервалом Найквиста.

Пусть преобразование Фурье X(f) некоторой реализации задано в интервале частот от -В до В Гц и равно нулю вне этого интервала. Интервал физически осуществимых частот составляет 0-В Гц. Обратное преобразование Фурье имеет вид:

(4)

Для того чтобы получить периодическую функцию частоты с периодом 2B Гц, положим, что функция X(f) непрерывно повторяется. Основное приращение времени составляет t = 1/2В. Теперь:

Где:

Из формулы (4) следует, что:

(5)

Таким образом, величина х(п/2В) определяет значения коэффициентов С_п и, следовательно, функцию X(f) при всех значениях f. Вид этой функции в свою очередь определяет ординаты x(t) при всех значениях t. Этот вывод составляет содержание теоремы о дискретном представлении процесса во временной области. Основное приращение времени 1/2В называется интервалом Найквиста.

Предположим теперь, что реализация х(t) задана только в интервале времени от 0 до Т секунд, а ее преобразование Фурье X(f) - в интервале частот от -В до В Гц. Это двойственное предположение теоретически невозможно в силу принципа неопределенности. В действительности, однако, оно может быть приближенно справедливо для конечных интервалов времени и для полосовых фильтров. Полагая, что на функции x(t) и Х (f) наложены такие ограничения, касающиеся интервалов времени и частот, можно показать, что для определения функции х(t) при всех значениях t необходимо знать лишь конечное число дискретных значений х(t) или Х(f). Согласно формуле (3), снимая дискретные значения функции X(f) в точках, разделенных по шкале частот коинтервалом Найквиста 1/Т в промежутке от --В до В, можно найти число дискретных значений, которое необходимо для описания функции x(t). Это число равно:

Согласно формуле (5), снимая дискретные значения функции х(f) в точках, разделенных по шкале времени интервалом Найквиста 1/2В в промежутке от 0 до T, можно найти, что:

Таким образом, требуется одинаковое число дискретных значений при выборке их через коинтервал Найквиста по шкале частот и при выборке через интервал Найквиста по шкале времени.