1.3. Переходные непериодические процессы

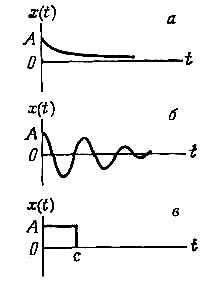
К переходным относятся все непериодические процессы, не являющиеся почти периодическими процессами, то есть процессами, частоты компонент которых несоизмеримы. Переходные процессы включают в себя все процессы, которые могут быть описаны подходящими функциями времени. Три примера переходных процессов приведены на рис. 4.

Рис. 4. Примеры переходных процессов

Физические явления, которым соответствуют переходные процессы, весьма многочисленны и разнообразны. Например, процесс, изображенный на рис. 4, «а» может описывать изменение во времени температуры воды в чайнике (относительно температуры воздуха в комнате) после выключения нагревателя. Кривая на рис. 4, «б»может характеризовать свободные колебания инерционной механической системы после прекращения действия вынуждающей силы. График на рис. 4, «в» может описывать изменение во времени напряжения в тросе, к концам которого приложена нагрузка и который разрывается в момент с.

Рис. 5. Спектры переходных процессов

Важное отличие переходных процессов от периодических и почти периодических процессов состоит в том, что их невозможно представить с помощью дискретного спектра. Однако в большинстве случаев получают непрерывное спектральное представление переходных процессов, используя интеграл Фурье:

•Спектр Фурье Х() в общем случае является комплексной функцией, которая может быть записана в показательной форме:

Здесь |X(f) | - модуль,  (f) – аргумент. Модули |X{f}| преобразования Фурье трех переходных процессов, изображенных на рис. 4, показаны на рис. 5.

2. Классификация случайных процессов

Функция времени, описывающая случайное явление, называется выборочной функцией (или при конечном интервале времени - реализацией). Множество всех выборочных функций, которые могут быть получены при регистрации данного случайного явления, называется случайным, или стохастическим, процессом. Следовательно, реализация, полученная в результате наблюдений над случайным физическим явлением, может рассматриваться как элемент множества возможных физических реализаций случайного процесса.

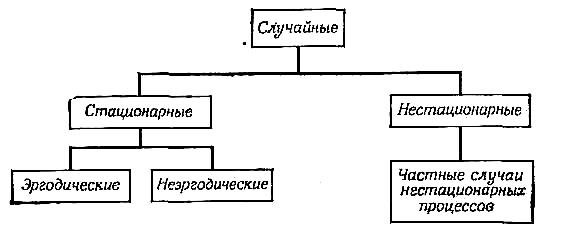
Рис. 6. Классификация случайных процессов

Различают стационарные и нестационарные случайные процессы. В свою очередь стационарные случайные процессы могут быть эргодическими или неэргодическими. Для нестационарных случайных процессов существует специальная классификация нестационарности. Связь между различными классами случайных процессов показана схематически на рис. 6. В последующих разделах мы обсудим в общих чертах значение и физический смысл различных классов случайных процессов.

2.1. Стационарные случайные процессы

Физическое явление при рассмотрении с позиций теории случайных процессов можно описать в любой момент времени путем осреднения величин по множеству выборочных функций, представляющих данный случайный процесс. Рассмотрим, например, множество выборочных функций (называемое также ансамблем), образующее случайный процесс (рис. 7).

Рис. 7. Ансамбль выборочных функций, формирующих случайный процесс.

Среднее значение (первый момент распределения) случайного процесса в момент времени t₁ может быть найдено путем суммирования мгновенных значений каждой выборочной функции ансамбля в момент t₁ и деления этой суммы на число выборочных функций. Аналогичным образом корреляция между значениями случайного процесса в два различных момента времени (смешанный момент, называемый автокорреляционной функцией) определяется путем осреднения по ансамблю произведений мгновенных значений процесса в моменты t₁ и t₁ + . Иначе говоря, среднее значение _x(t₁) и автокорреляционная функция R_x(t₁, t₁ + ) случайного процесса {x(t)} (фигурные скобки означают ансамбль выборочных функций) определяются из соотношений:

Причем при суммировании предполагается, что появление всех выборочных функций равновероятно.

В общем случае, когда функции _x(t₁) и R_x(t₁, t₁ + ), определяемые данными уравнениями, меняются с изменением момента времени t_1, случайный процесс {x(t)} называется нестационарным. В частном случае независимости _x(t₁) и R_x(t₁, t₁ + ) от t₁ случайный процесс {x(t)} называется слабо стационарным, или стационарным в широком смысле. Среднее значение слабо стационарных процессов постоянно, а автокорреляционная функция зависит только от величины сдвига , т. е. _x(t₁)=_x и R_x(t₁, t₁ + )= R_x().

Для случайного процесса {x(t)} можно рассчитать бесконечное множество начальных и смешанных моментов более высоких порядков; их совокупность полностью описывает плотности распределения процесса. Когда все начальные и смешанные моменты распределения не зависят от времени, случайный процесс {x(t)} называется строго стационарным, или стационарным в узком смысле. Для многих практических приложений доказательства слабой стационарности процесса вполне достаточно, чтобы оправдать справедливость предположения о строгой стационарности.