2.2. Эргодические случайные процессы

В предыдущем разделе был рассмотрен вопрос об определении свойств случайного процесса путем осреднения по ансамблю в отдельные моменты времени. Однако в большинстве случаев, возможно, также описать свойства стационарного случайного процесса путем осреднения по времени отдельных выборочных функций ансамбля. Рассмотрим, например, k-ю выборочную функцию случайного процесса, изображенного на рис. 7. Среднее значение _x(k) и автокорреляционная функция R_x( , k) этой выборочной функции определяются выражениями:

Если случайный процесс {x(t)} стационарен и определенные данными формулами _x(k) и R_x( , k) одинаковы для различных выбороч­ных функций, то случайный процесс {x(t)} называется эргодическим. Для эргодического случайного процесса среднее значение и автокорреляционная функция (а также и другие моменты, полученные осреднением по времени) равны соответствующим средним по ансамблю: _x(k)=_x и R_x( , k)=R_x(). Следует заметить, что только стационарные процессы могут обладать свойством эргодичности.

2.3. Моменты второго порядка (среднее значение квадрата и дисперсия)

Элементарное представление о суммарной интенсивности лю­бого случайного процесса дает среднее значение квадрата, которое представляет собой просто среднее из всех значений квадрата процесса в пределах данной реализации. Среднее значение квад­рата ² данной реализации x(t) определяется в виде:

Абсолютная величина корня квадратного из среднего значения квадрата называется среднеквадратичным значением.

Зачастую удобно рассматривать физический процесс в виде суммы статической, т. е. не зависящей от времени, составляющей и динамической, или флуктуационной, составляющей. Статиче­скую составляющую можно получить, вычисляя среднее значение, которое представляет собой просто среднее из всех значений процесса. Среднее значение равно:

Динамическая составляющая определяется дисперсией процесса - величиной, равной просто среднему квадрату отклонений его ординат от среднего значения. Дисперсия процесса равна:

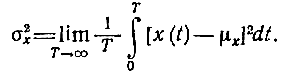
Положительное значение корня квадратного из дисперсии называется среднеквадратичным отклонением.

Раскрывая скобки в подынтегральной функции данной формулы находим, что дисперсия равна разности между средним значением квадрата и квадратом среднего значения

2.4. Автокорреляционная функция

Автокорреляционная функция случайного процесса характеризует общую зависимость значений процесса в некоторый данный момент времени от значений в другой момент. Рассмотрим реализацию x(t), приведенную на рис. 8.

Рис. 8. Определение автокорреляционной функции

Оценку величины автокорреляционной функции, связывающей значения x(t) в моменты времени t и t₁ + , можно получить, вычисляя произведение этих ординат и осредняя величину произведения в пределах времени наблюдения Т. Найденное среднее значение произведения приближается к точному значению автокорреляционной функции при стремлении Т к бесконечности:

Величина R_x() — всегда действительная четная функция с мак­симумом в точке =0; она может быть как положительной, так и отрицательной. Запишем эти утверждения в виде формул:

Среднее значение функции x(t) выражается через автокорреляционную функцию (исключая некоторые особые случаи, как, например, гармоническое колебание) выражается:

Таким образом, среднее значение функции x(t) равно положительному значению корня квадратного из автокорреляционной функции, взятой при очень большом сдвиге. Аналогично среднее значение квадрата функции равно:

т. е. среднее значение квадрата равно значению автокорреляцион­ной функции при нулевом сдвиге.

Примеры. На рис. 9 показаны типичные графики автокорреляционных функций (зависимости R от сдвига ). Эти гра­фики называются автокоррелограммами. Имеющая вид косинусоиды автокоррелограмма гармонического колебания (рис. 9,а) описывается соотношением:

Важная особенность этой автокоррелограммы заключается в том, что форма ее периодически повторяется во времени с тем же периодом, что и период рассматриваемого гармонического колебания, но информация о фазе теряется.

Автокоррелограмма, имеющая вид крутого пика с быстрым спаданием к нулю (рис. 9, г), типична для широкополосного случайного процесса с нулевым средним значением (если среднее значение не равно нулю, автокорреляционная функция стремится к величине _x²). В предельном гипотетическом случае белого шума (случайный процесс, энергия которого равномерно распределена по всем частотам) автокоррелограмма имеет вид дельта-функции Дирака при нулевом значении сдвига (=0).

Автокоррелограмма суммы гармонического колебания и случайного шума представляет собой просто сумму автокоррелограмм гармонического колебания и случайного шума (рис. 9, б). С другой стороны, автокоррелограмма узкополосного случайного шума (рис. 9, в) напоминает автокоррелограмму гармонического колебания с затухающей амплитудой. Важной ее особенностью является то, что она стремится к нулю при больших значениях сдвига (если _x=0). Четыре графика на рис. 9 показывают, как меняется вид автокоррелограмм при переходе от гармонического процесса к широкополосному случайному процессу.

Рис. 9. Графики автокорреляционных функций (автокоррелограммы)

а - гармонический процесс; б - сумма гармонического процесса и случайного шума; в - узкополосный случайный шум; г - широкополосный случайный шум.