Весна 16 курс 3 ОрТОР / Теория АД / Термодинамика и теплопередача Никифоров А.И.-3

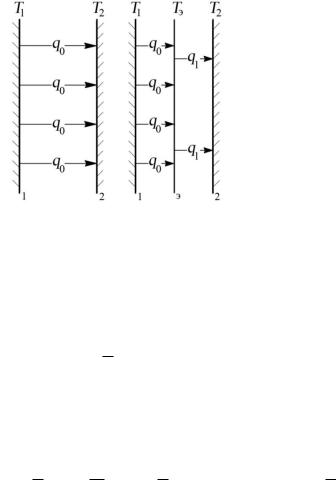
91

Когда между телами 1 и 2 будет установлен экран, то его температура примет некоторое значение Tэ, а количество теплоты, воспринимаемой экраном от тела 1, должно равняться количеству теплоты передаваемой экраном телу 2:

Рис. 11.4. Экран для защиты от излучения

Отсюда следует, что:

Tэ4 12 (T14 T24 ).

Подставляя это значение в формулу (11.11), найдём количество теплоты,

передаваемой телом 1 телу 2 при наличии одного экрана между ними:

q1 пр 0 (T14 12 T14 21 T24 ) 12 пр 0 (T14 T24 ) 12 q0 .

11.5. Теплообмен в замкнутой полости

Выше рассмотрен теплообмен между двумя плоскими параллельными поверхностями. Описанный метод можно применить и к поверхностям в замкнутом пространстве (рис. 11.5.).

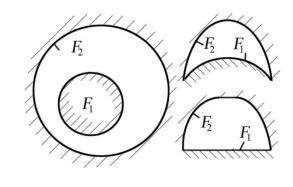
92

В этом случае тепловой поток между телами определяется формулой:

F1 – площадь наименьшей поверхности.

Рис. 11.5. К вопросу о теплообмене в замкнутой полости

11.6. Излучение газов и паров

Газы (азот, водород, кислород, воздух), в молекулах которых содержатся один или два одинаковых атома, полностью прозрачны для электромагнитного излучения при температуре ниже 10000 К. Лишь многоатомные газы, имеющие несимметричные молекулы, обладают способностью к поглощению (а, следовательно, и к излучению) электромагнитной энергии. Это такие газы, как водяной пар, углекислота, окись углерода, двуокись серы, аммиак, хлористый водород, углеводороды.

Наиболее важное значение для техники имеет излучение водяного пара

H2O и углекислоты CO2, которые всегда содержатся в продуктах сгорания. В отличие от твердых тел газы излучают и поглощают энергию не при любой длине волны, а лишь в пределах нескольких узких диапазонов волн, называемых полосами излучения (поглощения). Такое излучение называется избирательным,

93

или селективным. Твёрдые тела излучают и поглощают энергию волн всех длин волн: от λ = 0 до λ = ∞.

Полосы излучения (и поглощения) для паров H2O и CO2 (табл. 11.2) лежат в невидимой (инфракрасной) части спектра.

Таблица 11.2 Полосы излучения (и поглощения) для паров H2O и CO2

Проходя через слой поглощающего газа, интенсивность лучистого потока падает постепенно, в зависимости от концентраций CO2 и H2O, которые учитывают парциальным давлением, и в зависимости от толщины слоя газа.

Следовательно, второе отличие излучения газа от излучения твёрдого тела состоит в том, что твёрдое тело излучает (поглощает) энергию только поверхностью, газ – всем объёмом.

11.7. Излучение пламени

Характер излучения пламени зависит от типа сжигаемого топлива. Водород, окись углерода и ряд других газов горят почти бесцветным пламенем. Излучение такого пламени имеет характер чистого излучения и может быть рассчитано по методу, изложенным выше.

Большинство углеводородных топлив, в том числе авиационных, имеет светящееся пламя с жёлтоватой окраской. Это связанно, главным образом, с образованием большого количества мельчайших частичек углерода, которые являются источником данного свечения. Излучение такого пламени по своему характеру близко к излучению твёрдых тел; в частности, спектр его излучения

где ε1 и ε2 – степень черноты первого и второго тела; С0 – коэффициент излучения абсолютно чёрного тела.

В случае теплообмена между газом, имеющим температуру Тг, и стенкой количество переданного газом тепла стенке определяется по формуле

где ст = 0,5 ∙ (εст + 1) – эффективная степень черноты стенки;

εг – степень черноты газа при температуре стенки; εст – степень черноты стенки.

11.9. Лучисто-конвективный теплообмен

Часто лучистый теплообмен между газом и стенкой протекает одновременно с конвективным. В этом случае общая плотность теплового потока равна:

q qк qл ,

где qк и qл – конвективная и лучистая плотности теплового потока. Иногда формуле для определения qл придают вид формулы Ньютона:

qл л Tг Tст .

Тогда:

где αк – коэффициент теплопередачи конвективного теплообмена; αл – условный коэффициент теплоотдачи теплообмена излучением.

Из (11.10) и (11.17) следует:

97

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 11.1.

Определить собственную излучательную способность стенки летательного аппарата с коэффициентом излучения С = 4,53 Вт/(м2 · К4), если температура излучающей поверхности стенки 1027 °С. Найти также степень черноты стенки и длину волны, отвечающей максимуму интенсивности излучения.

Степень черноты стенки ε определяем из равенства:

С0 С ,

где C0 = 5,67 Вт/(м2 · К4) – коэффициент излучения абсолютно чёрного

тела.

Таким образом, степень черноты стенки ЛА равна:

Из курса физики известно, что длина волны, соответствующая максимуму интенсивности излучения определяется по закону Вина. Закон Вина определяет, что с ростом температуры спектральная плотность излучения смещается в сторону меньших длин волн:

m T b

где b = 2,9 · 10-3 (м · К) – постоянная Вина. Из последнего уравнения получаем:

98

Задача 11.2.

Две плоские поверхности [одна из динасового кирпича (ε1 = 0,97)] поддерживается при температурах: кирпичная T1 = 1273 К, стальная (ε2 = 0,8) T2 = 640 К. Расстояние между поверхностями мало по сравнению с их высотой и шириной. Найти величину лучистого теплового потока, отнесённого к единице поверхности.

Решение

Для замкнутой системы, состоящей из двух тел, расчётная зависимость по определению плотности лучистого теплового потока имеет вид (формула

11.15):

Найдём приведённую степень черноты εпр по формуле (11.9)

Теперь, подставляя известные величины в расчётную формулу, получим:

Задача 11.3

Определить лучистый теплообмен между стенками сосуда Дьюара, внутри которого хранится жидкий кислород, если на наружной поверхности внутренней стенки сосуда температура t1 = -183 °С, а на внутренней поверхности наружной стенки температура t2 = 17 °C. Стенки сосуда покрыты слоем серебра, степень черноты которого ε1 = ε2 = 0,02, площади поверхности стенки F1 F2 0,1м2 .