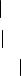
y′(0) = e0 − 0 = 1.

Дифференцируем уравнение и вычисляем последующие коэффициенты: y′′ = −ex − y′ x =0 = −1 − 1 = −2,

y′′′ = e−x − y′′ x =0 = 1 + 2 = 3,

y IV = −e−x − y′′′ x = 0 = −1 − 3 = −4,

На этом остановимся, поскольку по условию необходимо найти только пять ненулевых членов ряда.

Итак, решение имеет вид

или

3. РЯДЫ ФУРЬЕ

3.1. Ряды и коэффициенты Фурье

Определение 1. Разложение функции f(x) в ряд по тригонометрической системе функций cos0x, cosx, sinx, … называется тригонометрическим рядом Фурье.

Это разложение имеет вид

∞

f (x ) = ∑ (an cosnx + bn sin nx ) ,

n = 0

где an, bn называются коэффициентами Фурье для функции f(x) и являются функциями дискретного аргумента п = 0, 1, 2, 3, ….

Найдём формулы для вычисления этих коэффициентов.

∞

1. Умножим обе части равенства f (x ) = ∑ (an cosnx + bn sin nx ) на cos0x и проинтегрируем на

n = 0

отрезке [−π, π]. В силу ортогональности системы все слагаемые суммы обратятся в ноль, кроме одного, при n = 0:

28

Найти ряд Фурье для функции – значит: найти коэффициенты Фурье этой функции по формулам и записать тригонометрический ряд с этими коэффициентами.

Пример 1. Разложить в ряд Фурье функцию f(x) = |х| на [−π, π].

Воспользовавшись свойством аддитивности определённого интеграла, найдём коэффициенты разложения

29

3.2. Условия и теорема Дирихле

Выясним вопрос о том, в каких случаях ряд Фурье функции f(x) сходится к этой функции.

Теорема Дирихле. Пусть на отрезке [−π, π] задана ограниченная функция f(x), удовлетворяющая на этом отрезке следующим двум условиям:

1.Функция f(x) непрерывна или кусочно-непрерывна, т. е. имеет на этом отрезке лишь конечное число точек разрыва, причём только первого рода.

2.Функция f(x) монотонна или кусочно-монотонна, т. е. этот отрезок можно разбить на конечное число отрезков, на каждом из которых функция f(x) монотонно возрастает, или убывает, либо остаётся постоянной.

Тогда такая функция f(x) разлагается в соответствующий ей тригонометрический ряд Фурье, который сходится на этом отрезке, причём:

1) в каждой точке х = х0 непрерывности функции f(x) сумма ряда S(x) равна значению функции f(x) в этой точке: S(x 0 ) = f (x 0 );

30

3) в точках х = − π и х = π (на границах отрезка) сумма ряда равна среднему арифметическому правого предела f(x) в точке х = − π и левого предела f(x) в точке х = π :

S(− π ) = S(π ) = f (− π + 0)2+ f (π − 0) ;

4) на всяком конечном отрезке, свободном от точек разрыва функции f(x), ряд равномерно сходится к f(x).

Теорема Дирихле даёт достаточные условия разложимости функции f(x) в тригонометрический ряд. Условия 1 и 2 теоремы называются условиями Дирихле.

Замечание. Сумма ряда

∞

S(x ) = ∑ (an cosnx + bn sin nx )

n = 0

есть периодическая функция с периодом Т = 2π. Она определена на всей числовой оси, но описывает разлагаемую функцию f(x) только на сегменте [−π, π], поскольку за его пределами сумма ряда повторяет свои значения как периодическая функция, а значения функции f(x) не подчинены такому закону.

Вернёмся к примеру 1 и проверим выполнение условий теоремы Дирихле для функции у = | х | на сегменте [−π, π].

πмонотонна (см. рис. 1).

2.Вычислим значения суммы ряда в конечных точках отрезка [−π, π]:

т. е. на концах отрезка значения суммы ряда и функции одинаковы. 3. В точках непрерывности функции сумма ряда и значения функции должны совпадать.

Проверим это утверждение например для точки x = π2 (− π , π ) :

т. е. утверждение теоремы действительно выполняется:

f (π2 ) = S(π2 ).

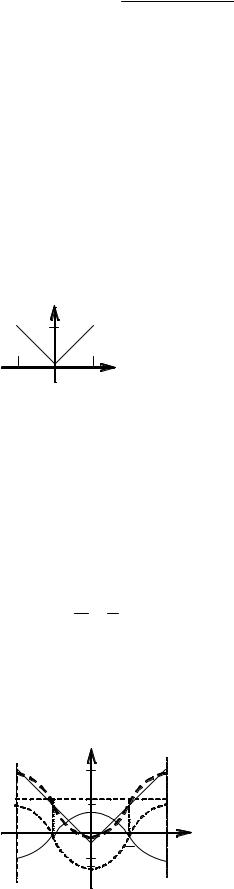
4. Построим частичные суммы ряда (см. рис. 1):

S0 (x ) = a20 = π2 , S1 (x ) = π2 − π4 cosx;

последнюю сумму строим методом суперпозиций:

y1 = cosx, y2 = − π4 y1 = − π4 cosx, y3 = y1 + y2 = π2 − π4 cosx,

S1 (± π ) = π2 + π4 — ориентировочные точки.

силу их равенства получаем

31