
- •1.1. Основные понятия
- •1.2. Свойства числовых рядов
- •1.3. Ряды с положительными членами
- •1.3.1. Достаточные признаки сравнения знакоположительных рядов. Эталонные ряды
- •1.3.2. Достаточные признаки Даламбера и Коши сходимости знакоположительных рядов
- •1.4. Ряды с произвольными членами
- •1.5. Знакочередующиеся ряды
- •2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- •2.1. Определение, область сходимости
- •2.2. Равномерная сходимость функционального ряда.
- •2.3. Степенные ряды
- •2.4. Разложение функций в степенные ряды
- •2.5. Приложения рядов к приближённым вычислениям
- •2.6. Решение задачи Коши с помощью степенных рядов
- •3. РЯДЫ ФУРЬЕ
- •3.1. Ряды и коэффициенты Фурье
- •3.2. Условия и теорема Дирихле
- •3.3. Разложение в ряд Фурье чётных и нечётных функций
- •3.5. Сдвиг сегмента разложения
- •3.6. Изменение длины сегмента разложения
- •3.7. Интеграл Фурье (как предельный случай ряда Фурье)
x |
dx |
|
x |
|
x |
|
x |
x |
||||
или ∫ |
= ∫ dx |
− ∫ x |
2dx + ∫ x 4dx + |
+ (−1)n ∫ x2ndx, |
||||||||
1 + x2 |
||||||||||||
0 |
|
|
0 |
|
0 |
|
0 |
|
|
0 |
||
arctg x = x − |
x 3 |
+ |
x 5 |
|
− |
+ (−1)n |
x 2n +1 |
|
+ . |
|||
3 |
5 |
|
2n + 1 |
|||||||||
|
|
|
|
|
|
|
|
|||||
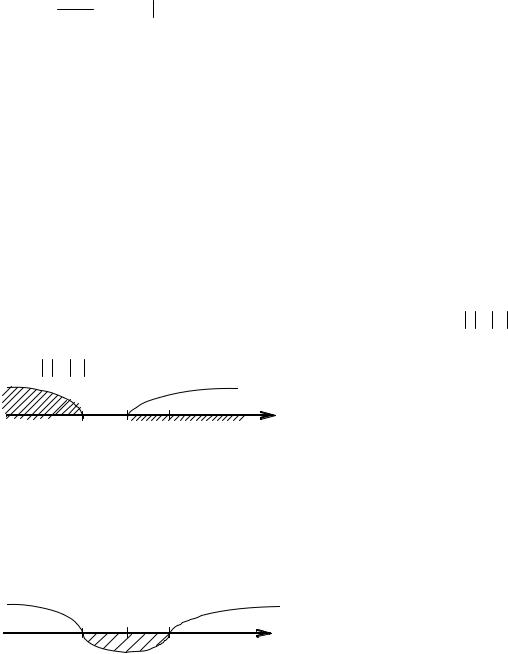
Итак, исходный ряд равномерно сходится на интервале (−1, 1) и его сумма равна
x
S(x ) = ∫ 1 +dxx 2 = ar ctg x 0x = arctg x .
0
Таким образом, зная сумму эталонного ряда, можно находить суммы других рядов, интегрируя или дифференцируя либо эталонный ряд, либо исходный, иногда эти операции приходится выполнять по несколько раз.
2.3. Степенные ряды
Определение 5. Степенным рядом называется функциональный ряд вида
∞
∑ an x n = a0 + a1x + a2x 2 + + an x n + ,
n = 0
где a0, a1, a2, …an , … — постоянные числа, называемые коэффициентами ряда, которые вычисляются по формуле ап = ϕ(п).
Областью сходимости степенного ряда всегда является некоторый интервал, который, в частности, может вырождаться в точку.
Теорема 2 (Абеля). Если степенный ряд сходится при некотором значении x0 , не равном нулю, то он абсолютно сходится при всяком значении х, для которого x < x0 .
Если ряд расходится при некотором значении x1 , то он расходится при всяком х, для которого x > x1 (см. рис..2).
Ряд расходится
Ряд сходится x0 |
x1 |
x2 |
x |
Рис. 2
Определение 6. Если на оси ох существует точка х = R > 0 (см. рис. 10.3), такая, что:
•ряд сходится для всех х : |х| < R ,
•ряд расходится для всех х : |х| > R,
то интервал (−R, R) называется интервалом сходимости ряда (10.3), а число R называется радиусом сходимости ряда. Точка х = 0 при этом называется центром сходимости.
На концах промежутка в точках |х| = |R| ряд может как сходиться, так и расходиться.
−R |
Ряд сходится |
R |
Ряд расходится |
0 |
Ряд расходится x |
|
Рис. 3 |
|
Для определения радиуса, а значит, и интервала сходимости используют уже известные нам признаки Даламбера и Коши. Покажем это.
∞
Рассмотрим ряд a0 + a1x + a2x 2 + + an x n + = ∑ an x n
n = 0
и ряд, составленный из абсолютных величин, т. е. ряд с положительными членами
|
a |
|
+ |
|
a x |
|
+ |
a x2 |
+ + |
a x n |
+ . |
|
|
|
|
||||||||
|
0 |
|
|
|
1 |
|
|
2 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
Применим к последнему признак Даламбера:
17
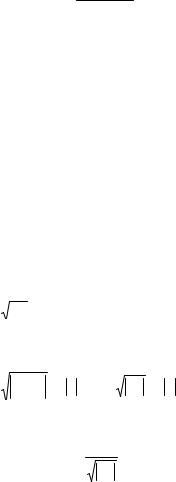
lim |
un + 1 |
= lim |
an + 1x n + 1 |
|
un |
an x n |
|||
n → ∞ |
n → ∞ |
По теореме Даламбера
|
= lim |
|
an + 1 |
|
x |
|
= z |
|
x |
|
. |
||||||
|
|
|
|
|
|||||||||||||
|
|
an |
|||||||||||||||
|
|
n → ∞ |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|||||||||||||
z |
|
x |
|
|
< 1 − ряд сходится, |
||||||||||||
|
|
||||||||||||||||
|
|
|
x |
|
|
> 1 |
− ряд расходится, |
||||||||||
|
|
|
|||||||||||||||
z |
|
|
|
||||||||||||||
|
|
|
x |
|
|
= 1 |
− ответа нет. |
||||||||||
z |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть z |x| < 1. Тогда ряд (10.9), а с ним (по теореме сравнения) и ряд сходится для всех
|
|
|
1 |
, т.е. на интервале |
|
|
1 |
|
1 |
|
. Но для всех |
|
|
z > 1 , т. е. для |
|
|
1 |
оба ряда |
|
|
|
|
|
|
|
|
|
||||||||||
x : |
x |
< |
z |
|
− |
z |
, |
z |
|
x : |
x |
x |
> |
z |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
расходятся, значит, |
1 |
= R — радиус сходимости, и найти его можно, вычислив предел |
||||
|
|
|
|
|
z |
|
|
an |
|
|
|
|
|
R = lim |
|
|
. |
|
|
|
an + 1 |
|
|
||||
n → ∞ |
|
|
|
|||
Для нахождения радиуса сходимости можно использовать и признак Коши, применявшийся ранее для знакоположительных числовых рядов:
|
|
|
q < 1 |
lim n u |
n |
= q, |
q > 1 |
n → ∞ |
|
|
|
|
|
|
|
|
|
|
q = 1 |
−ряд сходится,
−ряд расходится,
−ответа нет.
В нашей ситуации
lim n |
an x n |
= x lim n |
an = x z, |
n → ∞ |
|
n → ∞ |
|
т. е. ряд (10.3) сходится для всех x : |
|
x |
|
< |
1 |
и расходится, если |
|||||||
|
|
||||||||||||
|
x |
|
> |
1 |
, R = lim |
1 |
. |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
z |
n → ∞ n |
an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
Отметим частные случаи:
1)R = 0, степенной ряд сходится в единственной точке х = 0 и расходится на обеих полуосях оси ох;
2)R = ∞, ряд сходится в любой точке оси ох: х (−∞, ∞);
3)центром сходимости является какая-либо точка х = х0. Тогда имеем степенной ряд
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
a0 + a1(x − x0 ) + a2 (x − x0 )2 + + an (x − x0 )n + = ∑ an (x − x 0 )n . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n = 0 |
Применим признак Даламбера: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
lim |
|
an |
+ 1 (x − x |
0 )n + 1 |
|
= |
|
x − x |
|
|
lim |
|
an + 1 |
|
= |
|
x − x |
|
|
z, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
an (x − x 0 )n |
|
|
0 |
|
|
an |
|
|
0 |
|
|||||||||||||||
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x − x 0 |
|
z < 1, |
|
|
x − x 0 |
|
|
< |
1 |
, R = |
1 |
, |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
z |
z |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
−R < x − x 0 < R, −R + x 0 < x < R + x 0 .
В этом случае, выполняя обычную процедуру исследования по теореме Даламбера, получаем интервал сходимости (x0 – R, x0 + R), смещённый относительно начала координат. Исследование сходимости ряда в конечных точках x = ±R интервала сходимости (−R, R), если это требуется по условию задачи, проводится отдельно. Подставляя значения х1 = −R, x2 = R в исходный ряд, исследуем сходимость соответствующих числовых рядов, предварительно классифицируя их, т. к. выбор метода исследования зависит от того, какой ряд будет получен: знакоположительный либо знакочередующийся. И если к знакоположительным рядам можно применить несколько различных методов исследования на сходимость, то знакочередующийся ряд исследуется только с помощью теоремы Лейбница.
18
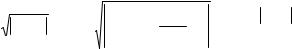
Пример 4. Найти радиус и интервал сходимости степенных рядов. Выяснить сходимость на концах интервала сходимости:
∞ |
|
|
x n |
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
n |
|
|
|
|
|
2 |
||||
4.1 ∑ |
|
|
|
|
; |
|
|
|
|
4.2. ∑(x − e) |
n n |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||
|
|
2 |
n |
|
|
|
|
|
n + 1 |
||||||||||||||||||
n =1 n |
|
|
|
|
|
|
|
|
|
n = 1 |
|
|
|
|
|
|
|
|
|||||||||
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! (x + 1)n |
|
|
|
|
|
|
|||
4.3. ∑n ! x |
|
n |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|||||||||||
|
|
; |
|
|
4.4. ∑ |
|
|
|
|
. |
|
|
|
|
|||||||||||||
|
|
(n + 1) |
n |
|
|
|
|||||||||||||||||||||
n = 1 |
|
|
|
|
|
|
|
|
|
|
|
n = 1 |
|
|
|
|
|
|
|
||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4.1. Используем признак Даламбера: |
|
|
|||||||||||||||||||||||||
an = |
|
1 |
|
, |
|
|
|
an + 1 = |
|
|
|
1 |
|
; |
|
|
|
|
|
|
|||||||
n |
2n |
|
|
|
(n + 1) 2n + 1 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
соответственно радиус сходимости |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
(n + 1) 2n 2 |
|
|
|
|||||||||
R = lim |
|
|
|
n 2n |
|
|
= lim |
|
= |
|
|
||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
n 2n |
|
|
|
|
|
|
|||||||||||
n → |
|
|
|
|
|
|
|
n →∞ |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
(n + 1) 2n +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
n + |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
= 2 lim |
|
|
|
|
|
|
= |
2 lim |
1 |
+ |
|
= 2 . |
|
|
|
|
|
|
|
|
|||||||
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
||||||||||||||
n →∞ |
|
|
|
|
|
n →∞ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Следовательно, данный ряд сходится при x (− 2, 2). Исследуем сходимость ряда на концах интервала сходимости.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
∞ |
|
При х = 2 наш ряд принимает вид ∑ |
2n |
= ∑ 1 — это гармонический ряд, он расходится. |
||||||||||||||||
n |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n =1 n 2 |
n =1 n |
|
Следовательно, точка х = 2 не входит в область сходимости ряда. При x = −2 имеем |
||||||||||||||||||
∞ |
|
|
n |
|
|
|
∞ |
n |
2 |
n |
|
∞ |
n |
|
||||
∑ |
|
(−2) |
|
= ∑ |
(−1) |
|
|
= ∑ |
(−1) ; |
|
||||||||
|
n |
|
n |
|
|
|
|
|
||||||||||
n =1 |
|
2 n |
|
|
n =1 |
2 n |
|
|
n =1 |
n |
|
|||||||
это знакочередующийся ряд, он сходится условно, т. к. выполняются условия теоремы |
||||||||||||||||||
Лейбница: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) a |
n + 1 |
< a |
n |
, |
|
1 |
|
< |
1 ; |
|
|
|
||||||
|
n + 1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||||
2) |
lim a |
n |
= 0, |
lim |
|
1 |
= 0. |
|
|
|
||||||||
|
n → ∞ |
|
|
|
|
|
n → ∞ n |
|
|
|
|
|
||||||
Значит, точка х = 2 принадлежит области сходимости степенного ряда. Окончательно: ряд сходится для всех х [−2, 2).
4.2. Применим признак Коши:
|
n |
|
|
(x − e) |
n |
n |
n2 |
|
|
|
x − e |
|
|
|
|
|
1 |
|
|
|
x |
− e |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
lim |
|
un (x ) |
= lim n |
|
|
|
|
= lim |
|
|
|
|
= |
= |
x |
− e |
lim |
|
|
|
= |
|
|
|
|
|
. |
|||||||
n → ∞ |
|
|
n → ∞ |
|
|
|
|
|
|
n |
+ 1 |
|
n → ∞ ( |
n + 1 |
)n |
|
|
|
|
n → ∞ (1 + |
1 |
)n |
|
|
|
e |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
|
|
|||||||||||||||
Ряд сходится, если |
|
|
x − e |
|
|
< 1, |
|
x − 1 |
|
< e, |
−e < x − e < e. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Радиус сходимости R = e, интервал сходимости 0 < x < 2e.
Исследуем сходимость в точках х = 0, х = 2е. Подставляя в исходный ряд х = 0, получим знакочередующийся числовой ряд
∞ |
(− 1) |
n |
|
n |
n |
n2 |
∑ |
|
e |
|
|
. |
|
|
|
|||||
n = 1 |
|
|
|
n + 1 |
|
|
19
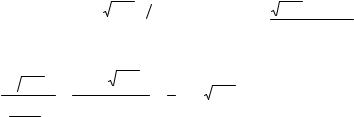
Исследуем его по признаку Лейбница:
lim |
an |
= lim |
n → ∞ |
|
n → ∞ |
|
en |
|
|
= 1 ≠ 0. |
n + 1 |
n n |
|||
|
n |
|
|
|
|
|
|
||
|
|
|
||
|
|
|
|
|
Ряд расходится.
Подставив в исходный ряд значение х = 2е, получим числовой знакоположительный ряд с общим членом
|
(2e − e)n n n2 |
|
n |
n |
n2 |
|
an = |
|
|
= e |
|
|
. |
(n + 1)n |
2 |
|
||||
|
|
|
n + 1 |
|
||
Его предел мы уже вычислили:
lim an = 1 ≠ 0,
n → ∞
т.е. необходимый признак сходимости не выполняется, числовой ряд расходится. Степенной ряд сходится только во внутренних точках интервала (0, 2e).
∞
4.3. ∑n! x n . Используем признак Даламбера:
n =1
an |
= n! , an +1 = (n + 1)! R = |
lim |
an |
= lim |
n! |
|
= |
|||||
|
(n + |
1)! |
||||||||||
|
|
|
|
|
|
|
n →∞ an +1 |
→∞ |
|
|||
= |
lim |
n! |
= |
lim |
1 |
= 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
n →∞ (n + 1)n! |
|
n →∞ n + 1 |
|
|
|
|
|
|
|
|||
т.е. наш ряд расходится при всех значениях х, кроме х = 0.
∞ |
n! (x + 1)n |
|
4.4. Найти область сходимости ряда ∑ |
(n + 1) |
n . |
n =1 |
|
|
Решение. Найдём радиус сходимости, применив признак Даламбера:
an = |
n! |
, an +1 = |
(n + 1)! |
, |
|
(n + 1)n |
(n + 2)n +1 |
||||
|
|
|
|
|
|
|
a |
|
|
|
|
n! (n + 2)n +1 |
|
|
|
||
R = |
lim |
n |
= lim |
|
|
|
|
|
= |
lim |
||||
|
|
|
|
|
|
|||||||||
|
|
n →∞ an +1 |
|
n →∞ (n + 1)n (n + 1)! |
n →∞ |
|||||||||
|
|
|
(n + 2)n +1 |
|
|
|
n + 2 |
n +1 |
|
|
|
|
||
= |
lim |
|
|
|
= |
|
lim |
|
= |
lim 1 + |
||||
|
|
|
|
|||||||||||
|
n →∞ (n + 1)n +1 |
|
n →∞ n + 1 |
|
|
n →∞ |
||||||||
|
(n + 2)n +1 n! |
= |
||
(n + 1)n n! (n + 1) |
||||
1 |
n +1 |
= e . |
|
|
|
|
|
|
|
|
n + 1 |
|
||
|
|
|
|
|
Следовательно, данный ряд сходится при −e < x + 1 < e , или −e − 1 < x < e − 1. Исследуем исходный ряд на сходимость в конечных точках интервала сходимости. При х = е − 1 имеем числовой положительный ряд
∞ |
|
n! (e − 1 + 1)n |
∞ |
|
n! en |
|
|
|
∑ |
|
|
= ∑ |
|
|
. |
||
(n + 1) |
n |
(n + 1) |
n |
|||||
n = |
1 |
|
n = |
1 |
|
|
||
|
|
|
|
|
||||
Для данного ряда не выполняется необходимый признак:
lim |
n! en |
= |
|
n! ≈ 2πn (n e)n |
|
= lim |
2πn en nn |
= |
|
|
|||||||
|
|
|
|
|
||||
n →∞ (n + 1)n |
|
|
формула |
|
n →∞ |
(n + 1)n en |
|
|
|
|
|
|
Стирлинга |
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim
n →∞
 2πn
2πn
n + 1 nn
|
lim |
2πn |
|
1 |
|
= ∞ . |
||
= |
n →∞ |
|
|
n |
= |
lim 2πn |
||
|
|
|
1 |
|
e n →∞ |
|
||
|
lim 1 |
+ |
|
|
|
|
|
|
|
n |
|
|
|
|
|||
|
n →∞ |
|
|
|
|
|
|
|
20
