21. Классы точности си.

По ГОСТ 16263-70 СИ - техническое средство, используемое при измерениях и имеющее нормированные метрологические свойства При использовании СИ принципиально важно знать степень соответствия информации о измеряемой величине, содержащейся в выходном сигнале, ее истинному значению. С этой целью для каждого СИ вводятся и нормируются определенные метрологические характеристики (MX). Метрологические характеристики — это характеристики свойств СИ, оказывающие влияние на результат измерения и его погрешности.

Класс точности — это обобщенная MX, определяющая различные свойства СИ. Класс точности СИ уже включает систематическую и случайную погрешности. Однако он не является непосредственной характеристикой точности измерений, выполняемых с помощью этих СИ, поскольку точность измерения зависит и от метода измерения, взаимодействия СИ с объектом, условий измерения и т.д.

В частности, чтобы измерить величину с точностью до 1%, недостаточно выбрать СИ с погрешностью 1%. Выбранное СИ должно обладать гораздо меньшей погрешностью, так как нужно учесть как минимум еще погрешность метода.

В связи с большим разнообразием как самих СИ, так и их MX, ГОСТ 8.401—80 устанавливает несколько способов назначения классов точности. При этом в основу заложены следующие положения:

1) в качестве норм служат пределы допускаемых погрешностей, включающие систематические и случайные составляющие;

2) основная погр δ_осн и все виды дополнительных погрешностей δ_доп нормируются порознь.

Первое положение свидетельствует о необходимости разрабатывать СИ с учетом однократного отсчета показаний по величине общей погрешности. Второе положение направлено на обеспечение максимальной

однородности однотипных СИ.

Классы точности присваивают СИ при их разработке по результатам государственных приемочных испытаний. Если СИ предназначены для измерения одной и той же физической величины, но в разных диапазонах, или — для измерения разных физических величин, то этим СИ могут присваиваться разные

классы точности как по диапазонам, так и по измеряемым физическим величинам.

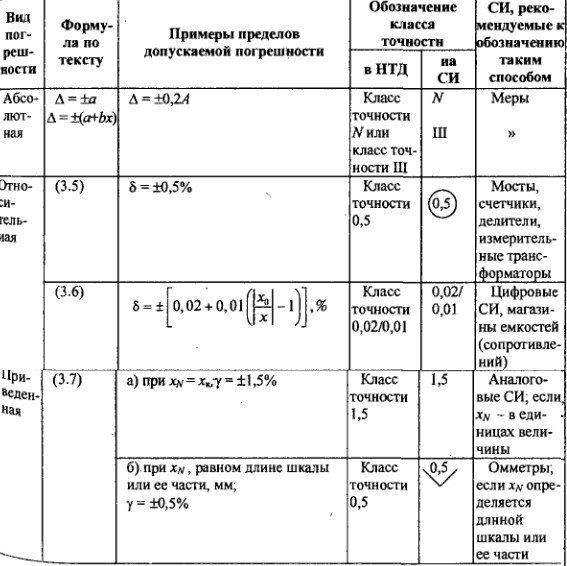
Если погрешность результатов измерений в данной области измерений принято выражать в единицах измерений величины или делениях шкалы, то принимается форма абсолютных погрешностей - три вида классов точности СИ:

• для пределов допускаемой абсолютной погрешности в единицах измеряемой величины или делениях шкалы;

• для пределов допускаемой относительной погрешности в виде ряда чисел δ= ±А*10ⁿ, где А= 1; 1,5; (1,6); 2; 2,5; (3); 4; 5 и 6; значения 1,6 и 3 допускаемые, но не рекомендуемые; n = 1; 0; -1; -2;...;

• для пределов допускаемой приведенной погрешности с тем же рядом: γ = ± А*10ⁿ

Класс точности через относительную погрешность СИ назначается двумя способами:

1. Если погрешность СИ имеет в основном мультипликативную составляющую, то пределы допускаемой основной относительной погрешности устанавливают по формуле

δ = ± Δ / х *100% = ± А*10ⁿ= ±q

2. Если СИ имеют как мультипликативную, так и аддитивную составляющие, то класс точности обозначается двумя цифрами, соответствующими значениям с и d формулы:

δ = ±[c + d (|x₀/x| - l)] Здесь с и d выражаются также через ряд, с – вначале, d – в конце.

22. Методы обработки результатов измерений. Многократные прямые равноточные измерения. Неравноточные измерения. Косвенные измерения. Алгоритм обработки косвенных измерений. Совместные и совокупные измерения.

Прямые многократные измерения делятся на равно- и неравноточные. Равноточными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той лее методике при неизменных внешних условиях. При равноточных измерениях СКО результатов всех рядов измерений равны между собой. Задача обработки результатов многократных измерений заключается в нахождении оценки измеряемой величины и доверительного интервала, в котором находится ее истинное значение. Обработка должна проводиться в соответствии с ГОСТ 8.207—76 "ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Общие положения".

Часто при исследовании и планировании измерительных операций приходится иметь дело с неравноточными измерениями (т.е. изм одной и той же величины с различной точностью разными приборами, в разных условиях и разными исследователями). Для оценки наиболее вероятного значения величины по данным неравноточных измерений вводят понятие веса измерения:

g = n_i / Ϭ_i² , где n_i и Ϭ_i ² – соотв объем и дисперсия i-той серии равноточных измерений. Тогда, если неравноточные измерения привели в результатам, где Xi – среднее арифм ряда равноточных измерений, то наиболее вероятностным значением будет среднее взвешенное:

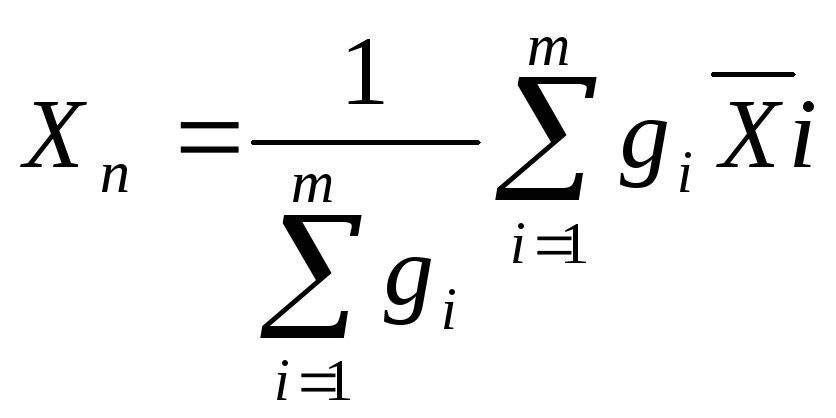
Косвенные измерения — это измерения, при которых искомое значение y находят на основании известной зависимости

y = f (x1, x2,…xn), где x1…xn – это подлежащие прямым измерениям аргументы функции y.

Алгоритм обработки косвенных измерений.

1.Для результатов прямых измерений аргумента Xi вычисляют выборочное среднее и выборочное стандартное

2.Для каждого аргумента вычисляют систематическую погрешность в виде СКО

характеризуют разброс результатов из-за субъективных причин (округление и др факторы)

3.Находят выборочное среднее функции

4.Вычисляют стандартное отклонение случайных и систематических погрешностей

5.Сравнивают

На практике:

Совместные и совокупные измерения.

Одновременное измерение двух или нескольких величин называется совместным, если уравнения измерения для этих величин образуют систему линейных независимых уравнений. Например

Если число уравнений > числа неизвестных, то систему решают методом наименьших квадратов и находят оценку x и y и их СКО. Доверительный интервал строят на основе распределения Стьюдента.

Совокупные измерения отличаются от совместных только тем, что при совокупных одновременно измеряю несколько одноименных величин. Матем аппарат один и тот же.