Практичні рекомендації

Алгоритми визначення власного вектора матриці

Алгоритм 1.

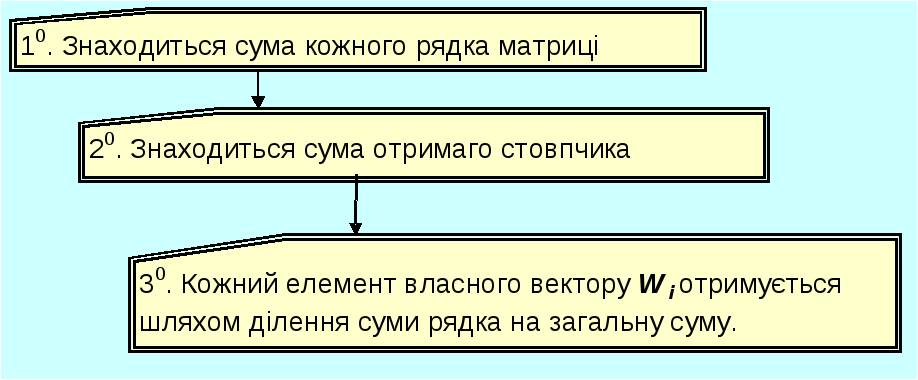
Алгоритм 2.

Алгоритм 3.

Алгоритм 4.

Знайдемо значення власного вектору кожної з матриць за першим алгоритмом (табл.3.16 –3.19).

Наведемо розрахунок елементів власного вектора за першим алгоритмом для матриці порівнянь критеріїв другого ієрархічного рівня:

1⁰.= 13;= 1,48;= 4,2.

2⁰.=13+1,48+4,2=18,68;

3⁰.; ; .

Таким чином, серед факторів, що порівнюються найбільший пріоритет відносно глобальної мети (загального добробуту держави), має економіка (вага -70%), далі йдуть соціальна інфраструктура (22%) та національна оборона (8%).

Розрахунки елементів власного вектору матриць для критеріїв третього рівня наведені в табл. 3.17-3.19.

Необхідні теоретичні відомості.

Узгодженість суджень перевіряється індексом узгодженості , який визначається через максимальне власне значення .

Матриця називається узгодженою, якщо максимальне власне значення матриці дорівнює порядку матриці .

Якщо , то в якості ступеня відхилення отриманої матриці від узгодженої визначається індекс узгодженості який не повинен перевищувати 0,1.

(3.17)

Максимальне власне значення визначається за залежністю:

, (3.18)

де - елементи власного вектору матриці, – елементи стовпчика, який являє собою результат множення рядків вихідної матриці порівнянь на стовпчик власного вектору.

Наведемо розрахунки та для матриці порівнянь критеріїв другого рівня. Розрахунки наведені в табл. 3.16.

Згідно з правилами множення матриці на стовпчик маємо:

10.7+70.08+50.22=2.36

0.7+10.08+0.22=0.25

0.7+30.08+10.22=0.6.

=

=

Аналогічно розраховуються індекси узгодженості та максимальні власні значення для третього рівня ієрархії (табл.3.17.-3.19.). Індекс узгодженості кожної матриці не перевищує припустимого значення, що свідчить про узгодженість суджень експертів.

Ієрархія цілей з визначеними пріоритетами наведено на рис. 3.10.

Рис. 3.10. Ієрархія цілей проблеми розподілу енергетичних ресурсів з визначеними пріоритетами.

3. Визначення суперкритерію – кількісного показника якості альтернативи.

Оцінка якості -ої альтернативи (галузь споживання) здійснюється за суперкритерієм, який визначається за залежністю:

(3.19)

де - відносна важливість-го критерію другого рівня,–важливість-ої альтернативи відносно–го критерія.

Для трьох альтернатив розподілення енергетичних ресурсів маємо:

Частка енергії, яка спрямовується у промисловість (=1)

=0,70,7+0,080,59+0,220,08 = 0,55

Частка енергії, яка спрямовується у транспорт (=2)

=0,70,24+0,080,34+0,220,22 = 0,24

Частка енергії, яка спрямовується у побутове споживання (=3)

=0,70,06+0,080,07+0,220,7 = 0,21

3. Вибір найкращої альтернативи.

Згідно з проведеним обґрунтуванням для забезпечення мети вищого рівня ієрархії – високого рівня добробуту держави у промисловість треба спрямувати 55% енергетичних ресурсів, на транспорт – 24%, на побутове споживання – 21% (табл.3.20).