
afanasev_v_n_optimalnye_sistemy_upravleniya_ana
.pdf
Заданная гладкая область определена соотношением
(x(t),t) 0, |
|
|
|
|
(2.70) |
||
где вектор (x(t),t) 1,..., q |
T |
|
q 1. |
||||
Rq , |
|||||||
Будем считать, что |
|
|
|
|
|
||
1) a (x,t), |
a (x,t) |
, |
a (x,t) |
, |
a 1,...,q непрерывны по x(t) и t; |
||
|
|
||||||
|
x(t) |
t |
|
|
|
|
|
2) векторы (градиенты) a (x,t) линейно независимы для всех (x,t) S.
x(t)
Пусть t0 - заданный начальный момент времени и x(t0 ) - заданное начальное состояние системы (2.68).
Функционал определим в виде
|
|
|
|
|
|
|
|
T |
|
|
|
(2.71) |
|
|
|
|
|
J(u) dt T t0 , |
|
||||||
где Т – свободно. |
t0 |
|
|
|
|
|||||||
|
|
|
|
|
||||||||
|
Задача заключается в нахождении такого u(t), которое |
|
||||||||||
|
удовлетворяет ограничениям (2.69); |
|
||||||||||
|
переводит x(t0 ) в область S; |
|
|
|||||||||
минимизирует функционал J(u) (2.71). |
|
|||||||||||
Гамильтониан системы имеет вид |
|
|
||||||||||
H(x,u, ,t) 1 T (t)[f (x,t) B(x,t)u(t)] |
(2.72) |
|||||||||||
1 T (t)f (x,t) T (t)B(x,t)u(t). |
|
|||||||||||
|
|
|||||||||||
Векторы x(t), (t) Rn |
образуют каноническую систему |
|
||||||||||
|
|
d |
|
|
H(x,u, ,t) T |
|
|
|||||
|
|
|
x(t) |
|
|
|
, |
|
|
|||
|
|
dt |
|
|
(t) |
|
|
|||||
|
|
|
|
|
|
|
(2.73) |
|||||
|
|
d |
|
|
|
H(x,u, ,t) T |
|
|||||
|
|
|
|
|
|
|
||||||
|
|
|
(t) |
|
|
|
. |
|
|
|||
|
|
dt |
|
x(t) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
Предположим, что u0 (t) -управление оптимальное по быстродействию, |
|||||||||||
выполняющее требования 1 и 2; |
x0 (t) - оптимальная траектория и T0 - |
|||||||||||
минимальное |
время |
окончания |
переходного процесса |
x(t0 ) S. По |
||||||||
определению оптимальные величины должны удовлетворять условиям |
||||||||||||
|
|
u0j (t) |
|
1, j 1,...,r, |
|
|
|
(2.74) |
||||
|
|
|
|
|
|
|||||||
|
|
x0 (t0 ) x(t0 ), |
|
|
|
|
||||||
|
|
x0 (T0 ) S. |
|
|
|
|
|
|||||
Третье условие из (2.74) в силу (2.70) означает, что |
(2.75) |
|||||||||||
|
(x0 ,T0 ) 0. |
|
|
|
||||||||
Из принципа максимума (минимума) имеем |
(2.76) |
|||||||||||
H(x0 ,u0 , 0 ,t) min H(x0 ,u, 0 ,t), t [t0 ,T] |
||||||||||||
u U
или, эквивалентно,
53
H(x0 ,u0 , 0 ,t) H(x0 ,u, 0 ,t), u(t) U, |
t [t0 ,T]. |
Учитывая (2.68) и (2.72), последнее неравенство можно переписать:
1 [ 0 (t)]T f (x0 ,t) [ 0 (t)]T B(x0 ,t)u0 (t)
n |
r |
n |
|
|
1 fi (x0 ,t) i0 (t) u0j (t) bi j (x0 |
,t) 0i (t) |
|||
i 1 |
j 1 |
i 1 |
|
|
n |
r |
n |
|
|
1 fi (x0,t) 0i (t) uj (t) bi j (x0 |
,t) 0i (t) . |
|
||
i 1 |
j 1 |
i 1 |
|
|
(2.77)
(2.78)
Так как первые члены с обеих сторон неравенства равны, то
r |
|
n |
|
|
r |
n |
|
(2.79) |
||||||||||
u0j |
(t) bi j (x0 ,t) i0 |
(t) uj (t) bi j (x0 ,t) 0i (t) |
||||||||||||||||
j 1 |
|
i 1 |
|
|
j 1 |
i 1 |
|
|
||||||||||
для всех u(t) U, t [t0 ,T]. |
|
|
|
|
|
|
|
|||||||||||
Введем обозначение |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
g0j (t) bi j (x0 ,t) i0 (t), j 1,...,r |
|
|
||||||||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
||
или в векторной форме |
|
|
|
|
|
|
(2.80) |
|||||||||||
|
|
g0 (t) BT (x0 ,t) 0 (t), |
g(t) Rr . |
|
||||||||||||||
|
При использовании функции g0 (t) неравенство (2.79) запишется в виде |
|||||||||||||||||
|
|
r |
|
r |
|
|
|
|
|
|
|
|||||||
|
u0j (t)g0j (t) |
uj (t)g0j (t) |
|
|
|
(2.81) |
||||||||||||
|
|
j 1 |
|
j 1 |
|
|
|
|
|
|
|
|||||||
для всех |
|
|
uj (t) |
|
1, j 1,...,r и любого t [t0 ,T]. |
|
|
|||||||||||
|
|
|
|
|||||||||||||||
Уравнение (2.81) означает, что функция |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
(u(t)) uj (t)g0j (t) |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
достигает абсолютного минимума при |
|
|
||||||||||||||||
|
uj (t) u0j (t). |
|
|
|
|
|
|
|
|
|
|
|||||||
При этом справедливо соотношение |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
r |
|
|
|
|
r |
|
|
|
|
|
min (u(t)) min |
uj |
(t)g0j (t) |
min |
uj (t)g0j (t). |
|
(2.82) |
||||||||||||
u U |
|
|
|
|
u U |
j 1 |
|
|
|
j 1 |
u j(t) |
1 |
|
|
||||
|
Замена местами min и знака возможна, так как функции u1(t),...,ur (t) |
|||||||||||||||||
ограничены независимо друг от друга. Отметим, что |
|
|||||||||||||||||
|
|
min |
uj (t)g0j (t) |
|
g0j (t) |
|
. |
|
|
|
(2.83) |
|||||||
|
|
|
|
|
|
|
||||||||||||
|
|
uj (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Управления ui0 (t)будут минимизировать функцию uj (t)g0j (t).Следовательно, в
силу условия (2.82), управление u0j (t) должно быть функциями g0j |
(t) вида |
|||
u0j |
(t) 1, |
если g0j |
(t) 0; |
|
u0j |
(t) 1, |
если g0j |
(t) 0; |
(2.84) |
u0j |
(t)неопределенно, если g0j (t) 0. |
|
||
Выражения (2.84) можно записать в виде
54
u0j (t) sign g0j |
(t) |
|
|
|
(2.85) |
|
n |
|
j 1,...,r, t [t0 ,T]. |
|
|
||
sign bi j (x0 ,t) i0 (t) , |
|
|
|
|
||
i 1 |
|
|
|
|
|
|
Уравнение (2.85) показывает, что оптимальное по быстродействию |
||||||
управление u0 (t) есть вполне определенная функция от |
x0 (t), 0 (t)и t, если |
|||||
аргумент sign не равен нулю. Однако при |
g0j (t) 0 |
величину |
u0j (t)из |
|||
уравнения (2.85) определить нельзя. |
|
|
|
|
||
Выделим два случая: первый назовем нормальным, а второй – |
||||||
вырожденным. |
|
|
|
|
|
|
Определение. Нормальная задача об оптимальном быстродействии. |
|
|||||
Предположим, что на интервале [t0,T] имеется счетное количество |
||||||
точек t1,t2 ,t3,..., |
|
|
|
|
|
|
таких, что ta j [t0 ,T], a 1,2,3,...; j 1,...,r |
|
|
|
|
||
n |
|
0 втом итольковтомслучае,еслиt t |
|
; |
|
|
g0j (t) bi j (x0 ,t) i0 (t) |
не равнанулювовсехдругихслучаях. |
a j |
|
|
||
i 1 |
|
|
|
|
||
В этом случае задачу об оптимальном быстродействии называют |
||||||
нормальной. |
|
|
|
|
|
|
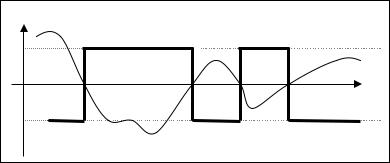
На рис |
2.4 показана функция g0j (t) и соответствующее управление |
|||||
u0j (t), найденное по уравнению (2.85). Функция |
g0j (t)равна нулю только в |
|||||
изолированные моменты времени, и поэтому управление, оптимальное по |
||||||
быстродействию, есть кусочно-постоянная функция с переключениями. Если |
||||||
все функции |
g0j (t)имеют такие же свойства, то задача |
управления |
будет |
|||
нормальной. |
|
|
|
|
|
|
g0 (t) |
|
|
|
|
|
|
|
u0 (t) |
|
|
|
|
|
|
t |
|
|
|
|
|
Рис. 2.4. Функция g0j (t) |
полностью определяет управление u0j (t) |
|
||||
Определение. Вырожденная задача об оптимальном быстродействии. |
||||||
Предположим, на интервале [t0,T] есть один (или более) подынтервал |
||||||
[T1,T2] из [t0,T] такой, что |
|
|
|
|
||
n |
|
|
|
|
|
|
g0j (t) bi j (x0 ,t) i0 (t) 0, t [T1,T2 ]. |
|
|
|
|
||
i 1 |
|
|
|
|
|
|
Такую задачу называют вырожденной, а интервал [T1,T2] (или полуинтервал) |
||||||
– интервалом вырожденности. |
|
|
|
|
||
55

|
t |
u0 (t) |
g0 (t) |
Рис. 2.5. Вырожденная задача об оптимальном быстродействии
Функция g0j (t), показанная на рис. 2.5, равна нулю для всех t [T1,T2 ] и
поэтому соответствует вырожденной задаче. Таким образом, в случае вырожденной задачи существует, по крайней мере, один подынтервал времени, в течение которого уравнение (2.85) не определяет оптимального управления как функцию x0 (t) от и 0(t).
Последнее утверждение не означает, что оптимальное по быстродействию управление не существует или не может быть определено. Оно лишь означает, что необходимое условие (2.77) не дает определенного
соотношения между u0 (t),x0 (t), 0 (t),t . |
Вырожденные |
задачи будут |
рассматриваться в главе 6. |
|
|
Из уравнения (2.85), которое можно записать в виде |
(2.86) |
|
u0 (t) SIGN[BT (x0 ,t) 0(t)], |
|
|
следует, что оптимальное по быстродействию управление для рассматриваемой задачи есть кусочно-постоянные (или релейные) функции времени. Это обстоятельство, вытекающее из необходимых условий оптимальности, позволяет ограничить поиск оптимальных управлений классом uj (t) 1, j 1,...,r.
Еще раз отметим, что гамильтониан
H(x,u, ,t) 1 T (t)[f (x,t) B(x,t)u(t)]
идифференциальные уравнения, образующие каноническую систему
d |
H(x,u, ,t) T |
|
||||
|
x(t) |
|
|
|
, |
|
dt |
|
(t) |
||||
|
|
|
|
|||
d |
|
H(x,u, ,t) T |
||||
|
(t) |
|
|
|
, |
|
dt |
x(t) |
|
||||
|
|
|
|
|
||
полностью определенную объектом (2.68) и функционалом (2.71) и, таким образом, не зависит от граничных условий при t0 и области S. H- минимальное управление (2.86) функционально независимо от наложенных ограничений. Необходимые условия для гамильтониана и дополнительной переменной в конечный момент времени Т0 вместе с заданным начальным состоянием x(t0 ) x0 , условиями, задаваемыми на правом конце для дополнительной переменной
56

(T) q k k (x,T) , k 1 x(T)
и уравнениями, определяющими область конечных значений системы (2.70), дают достаточно граничных условий для решения 2n дифференциальных уравнений.
Вобщем случае управлений, при которых выполняются необходимые условия оптимальности, может быть несколько. Эти управления называются экстремальными. Каждое экстремальное управление дает траекторию, которая может быть оптимальной либо локально, либо глобально.
Всилу этого отметим следующее:
1.Если оптимальное управление u0 (t) существует и единственно и нет других локальных оптимальных управлений, то существует только одно экстремальное управление, которое и является оптимальным по быстродействию. Предположение об отсутствии других локальных оптимальных управлений превращает принцип минимума в необходимое и достаточное условие.
2.Если имеется m1 различных оптимальных управлений и если есть m2 управлений, оптимальных локально, но не являющихся оптимальными глобально, то всего будет m1+ m2 экстремальных управлений.
3.Из существования экстремальных управлений не вытекает необходимость существования глобально оптимального управления.
4.Если оптимальное по быстродействию управление существует, то его можно найти, вычислив время Т, требуемое каждым из
экстремальных управлений, и выбрать управление, минимизирующее Т.
Для произвольных нелинейных систем и областей S в общем виде получить ответ на вопросы:
существует ли управление, оптимальное по быстродействию?
единственно ли оптимальное управление?
является ли задача нормальной?
не содержится ли дополнительной информации в необходимых условиях для данных объекта и области его конечных значений?
невозможно. Имеется, однако, ряд результатов, полученных при исследовании линейных систем, которые будут рассмотрены в главе 5.
§ 2.6. Задача на оптимум расхода ресурсов
Как и в предыдущем разделе, объект описывается дифференциальным уравнением вида
d |
x(t) f (x,t) B(x,t)u(t), x(t) Rn , u(t) Rr . |
(2.87) |
|
||
dt |
|
|
57
Компоненты вектора управления u1,…,ur ограничены по величине
uj (t) |
1, |
j 1,...,r, или в векторной форме: u(t) U. |
Заданная гладкая область конечных значений состояния S определяется
соотношением |
l (x,t) 0, l 1,...,n k, k 1, или в |
векторной форме |
||
(x,t) 0, Rn k . |
Предположим, что область конечных значений |
|||
удовлетворяет предположениям, сделанным в § 2.5. |
|
|||
Функционал качества задан в виде |
|
|||
T |
r |
uj (t) |
|
(2.88) |
J(u) cj |
dt, cj 0. |
|||
t0 j 1 |
|
|
|
|
Таким образом, функционал (2.88) оценивает «стоимость» ресурсов, затрачиваемых на управление объектом (2.87).
Синтезируемое управление u(t) должно:
1.удовлетворять заданным ограничениям;
2.переводить систему из состояния x(t0) в область S;
3.минимизировать функционал (2.88):
если Т не задано; если Т фиксировано.
Рассмотрим вначале случай 2.1 (Т не задано). Образуем гамильтониан:
H(x,u, ,t)
r |
|
|
|
|
(2.89) |
cj |
|
uj (t) |
|
T (t) f (x,t) T (t)B(x,t)u(t). |
|
|
|
||||
j 1 |
|
|
|
|
|
Предположим, что управление u0 (t) U оптимальное в смысле минимума функционала (2.88) и x0(t) – соответствующая ему траектория и T - первый момент времени, когда x0 (T) S . Отметим, что если Т0 – минимальное время прибытия состояния в область S, то T T0.
Векторы x(t), (t) |
|
образуют каноническую систему, связанную с |
||||
основной задачей: |
|
|
||||
|
d |
H(x,u, ,t) T |
||||
|
|
x(t) |
|
|
|
, |
|
dt |
|
(t) |
|||
|
|
|
|
|||
|
d |
|
H(x,u, ,t) T |
|||
|
|
(t) |
|
|
, |
|
|
dt |
x(t) |
|
|||
|
|
|
|
|
||
или в координатной форме:
. |
|
|
|
|
|
|
|
r |
|
|
|
|
x k0(t) fk (x0,t) bk j (x0,t)u0j (t); |
||||||||||||
|
|
|
|
|
|
|
j 1 |
|
|
|
||
. |
|
|
|
n |
fi (x |
0 |
,t) |
|
|
|||
|
0(t) |
|
|
0 (t) |
||||||||
|
0 |
|
|
|
||||||||
|
k |
|
|
(t) |
|
k |
||||||
|
|
|
|
i 1 |
|
xk |
|
|
|
|||
|
r |
|
|
n |
b |
j |
|
|
|
|
||
|
|
u0 (t) |
|
i |
|
0 |
(t), k 1,...,n.. |
|||||
0 |
|
|
|
|||||||||
|
j |
|
|
|
|
|
k |
|
||||
|
j 1 |
|
|
i 1 |
xk (t) |
|
|
|
||||
(2.90)
(2.91)
Из принципа минимума Понтрягина следует, что
H(x0 ,u0 , 0 ,t) H(x0 ,u, 0 ,t), u(t) U, t [t0 ,T].
58

Учитывая это, будем иметь
r
cj u0j (t) { 0 (t)}T [f (x0 ,t) B(x0 ,t)u0 (t)]
j 1 |
|
|
r |
|
|
cj |
u0j (t) |
{ 0 (t)}T [f (x0 ,t) B(x0 ,t)u(t)], |
j 1 |
|
|
которое дает соотношение
r r
cj u0j (t) u0j (t
j 1 j 1
r |
|
r |
cj |
uj (t) |
uj |
j 1 |
|
j 1 |
n |
|
|
|
) bi j (x0 |
,t) 0i (t) |
|
|
i 1 |
|
|
(2.92) |
n |
|
|
|
|
,T]. |
||
(t) bi j (x0 ,t) 0i (t) , u(t) U, t [t0 |
|||
i 1 |
|
|
|
Для задачи с заданным временем окончания переходного процесса и движущимся множеством целей принцип минимума определяет значение гамильтониана при t T :
|
n k |
|
|
|
i (x ,T) |
|
|
||
H(x ,u , ,T) i |
. |
(2.93) |
||
|
i |
T |
|
|
Кроме того, для этого типа задач краевое условие на правом конце для переменной (t) имеет вид
|
|
n k |
0 |
(T) |
|
i 1
|
0 |
,T) |
|
|
|
i |
i (x |
. |
(2.94) |
||
|
|||||
|
x(T) |
|
|
||
В (2.92) и (2.93) i , i i-1,…,n-k - некоторые постоянные.
Рассматриваемая задача имеет решение, когда заданное время окончания переходного процесса T больше или равно минимальному времени окончания переходного процесса Т0 (т.е. T T0 ). Таким образом, если оптимальное по расходу ресурсов управление существует, то соответствующие траектории должны удовлетворять следующим условиям:
а) если Т не задано, то необходимые условия выражаются соотношениями (2.90), (2.91), (2.92), (2.94);
б) если T задано, то необходимые условия выражаются соотношениями (2.90), (2.91), (2.92), (2.94), однако заданное время не может быть меньше, чем минимальное время, находимое в задаче о быстродействии при минимуме расхода ресурсов.
Как это уже делалось в § 2.5, используя выражение (2.92), получим уравнение, связывающее оптимальное по расходу ресурсов управление с траекторией системы, соответствующей 0 (t).
Определим функцию q(t) Rr |
в виде |
q0 (t) B(x0 ,t) 0 (t). |
(2.95) |
Выражение (2.92) с учетом (2.95) можно переписать в виде
59

r |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
qj |
(t) |
|
|
|
|
|||||
сj |
uj |
(t) |
uj |
(t) |
|
|
|
|
|
|
|
|
|
||||
|
c |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
||
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.96) |
|
r |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qj |
(t) |
|
|
|||
сj |
uj |
(t) |
uj (t) |
|
|
|
|
|
|
, u(t) U, t [t0 |
,T]. |
||||||
|
|
c |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выражение (2.96) означает, что
n |
|
|
|
|
|
|
|
u0j |
(t) |
u0j |
|
cj |
|||||
j 1 |
|
|
|
|
|
n |
|
|
|
||
|
|
|
|
|
uj |
cj min |
|||||
i 1 |
|
u(t) U |
|
||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
n |
|
|||
(t) |
qj |
(t) |
min |
cj |
|||||||
|
|
|
|
||||||||
c |
|
|
|||||||||
|
|
j |
|
|
|
u(t) U |
|
||||
|
|
|
|
|
|
|
|
j |
1 |
||
|
|
|
|
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
qj (t) |
|
|
|
|
(t) |
uj |
(t) |
|
. |
|||||||
cj |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
uj (t)
|
0 |
|
|
|
|
uj |
(t) |
qj |
(t) |
|
|
|
|
|
|||
c |
|
||||
|
|
|
|
|
|
|
|
|
j |
|
|
Нетрудно видеть, что
|
|
|
|
|
|
|
|
|
0 |
|
|
|
min |
|
|
uj |
(t) |
uj (t) |
qj |
(t) |
|
||||
|
|
|
|
|
|
|||||||
|
|
c |
|
|||||||||
uj (t) |
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
(t) |
|
j |
|
||||
|
|
|
|
|
|
|
|
|||||
|
0, |
если |
qj |
1, |
(2.97) |
|||||||
|
|
|
||||||||||
cj
|
|
|
q0j (t) |
|
q0j (t) |
|
|
|
|
|
|||||
1 |
|
|
, если |
1. |
|||
|
|
||||||
|
|
|
cj |
|
cj |
|
|
|
|
|
|
|
|||
|
|
|
|
|
Так как минимум имеет место при u(t)=u0(t), то находим, что u0j(t)
связано с q0j(t) |
и, следовательно, с x0(t) и 0 (t) |
по (2.92) следующим образом: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
q |
0 (t) |
|
|
|
|
|||||
uj (t) 0, |
|
|
|
|
если 1 |
|
|
j |
|
|
1, |
|
|
|
|
|||||||
|
|
|
|
|
cj |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
q0 |
(t) |
|
|
|
|
|
|
|
|
|
||||
uj (t) 1, |
|
|
|
|
|
если |
|
|
j |
|
|
1, |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
cj |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
q0 |
(t) |
|
|
|
|
|
|
|
|
(2.98) |
||||
uj (t) 1, |
|
|
|
|
|
если |
|
|
j |
|
|
1, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
cj |
|
|
|
|
|
|
|
|
|
|||
0 uj (t) 1, |
|
|
|
если |
|
q0j (t) |
|
1, |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
cj |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
q |
0 (t) |
|
|
|
|
|
|
|
||||
1 uj (t) 0, |
|
|
|
если |
|
|
|
j |
|
1. |
|
|
|
|
||||||||
|
|
|
|
|
|
cj |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Соотношения (2.98) в компактной форме записываются в виде |
||||||||||||||||||||||
0 |
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
n |
0 |
0 |
|
|
||||
qj |
(t) |
|
|
|
|
|
bi j |
|
(2.99) |
|||||||||||||
uj (t) dez |
|
|
|
|
|
dez |
|
|
|
(x |
,t) i |
(t) |
||||||||||
|
c |
|
|
c |
|
|||||||||||||||||
|
|
j |
|
|
|
|
|
|
|
j |
i 1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или в векторной форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
u0 (t) DEZ C 1BT (x0 ,t) 0 (t) , |
|
|
|
(2.100) |
||||||||||||||||||
где
60
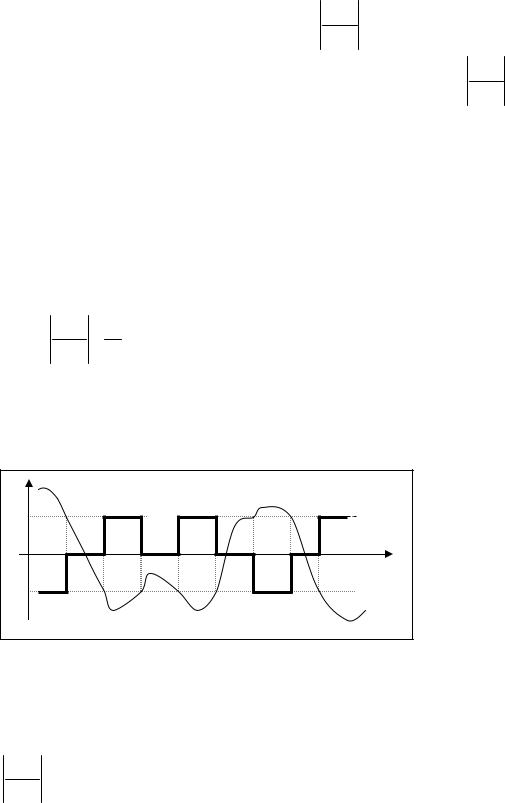
с1 |
0 |
|
|
0 |
|
|
|
|
|
|
|
||||
|
0 |
с2 |
|
|
0 |
|
|
|
|
|
|
|
|
||
С |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сr |
|
|
|
|
|
|
|
||||||
Из (2.98) |
видно, что |
|
|
q |
0 |
(t) |
|
|
|
|
|||||
|
если функция |
j |
1,то оптимальное по расходу |
||||||||||||
|
|
|
|
|
|
|
|
|
|
cj |
|
|
|
|
|
ресурсов управление полностью |
определено, |
если же |
q0 |
(t) |
то можно |
||||||||||
j |
1, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cj |
|
|
лишь угадать знак при управлении, само же оптимальное по расходу |
|||||||||||||||
ресурсов управление найти нельзя. Это обстоятельство приводит к понятию |
|||||||||||||||
нормальной и вырожденной задач на оптимум расхода ресурсов. |
|
||||||||||||||
Определение. |
|
Нормальная |
задача |
на |
оптимум |
расхода |
ресурсов |
||||||||
(рис.2.6). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предположим, что на интервале [t0,T], когда время переходного |
|||||||||||||||
процесса не задано, |
|
или на интервале |
[t0 ,T] |
при фиксированном времени |
|||||||||||
имеется счетное множество моментов времени 1,...., [t,0 T] или [t,0 T] таких, |
|||||||||||||||
что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q0j (t) |
|
1 |
|
n |
|
0 |
|
0 |
|
|
|
|
|
|
|
cj |
cj |
bij (x |
|
,t) i (t) 1 |
|
|
|
|
|
|
|
||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
||
в том случае, если t k , k 1,..., . |
Тогда задачу на оптимум расхода ресурсов |
||||||||||||||
будем называть нормальной. Моменты времени k называют моментами |
|||||||||||||||
переключений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
g0 (t)/с |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
u0 (t) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
Рис. 2.6. Нормальная задача на оптимум расхода ресурсов |
|
|
|
||||||||||||
В этом случае оптимальное по расходу ресурсов управление есть кусочно-постоянная функция времени, а ее значения +1 или –1.
Очевидно, что вырожденная задача возникает в том случае, если
0
qj (t) 1 в течение конечного интервала времени. cj
61
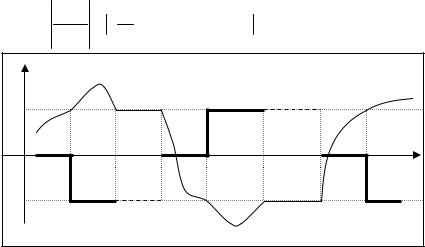
Определение. Вырожденная задача на оптимум расхода ресурсов
(рис.2.7).
Предположим, что на интервале [t0,T], когда время переходного процесса не задано, или на интервале [t0 ,T] при фиксированном времени имеется один (или более) подынтервал [T1,T2] такой, что
q0j (t) |
1 |
n |
0 |
0 |
(t) |
1, t [T1,T2 ]. |
|
cj |
bij (x |
|
,t) i |
||
cj |
i 1 |
|
|
|
|
|
|
g0 (t)/c |
|
|
|
|
|
|
|
t |
|
|
|
|
u0 (t) |
|
|
|
|
|
|
Рис. 2.7. Вырожденная задача на оптимум расхода ресурсов |
||||||
Такую задачу называют вырожденной, а интервал [t0,T] интервалом вырожденности. Последнее не означает, что оптимального по расходу ресурсов управления не существует. Это лишь означает, что необходимое условие, выраженное в виде принципа минимума (максимума) Понтрягина, не позволяет установить однозначно соответствие между оптимальным по расходу ресурсов управлением с траекторией системы и дополнительной переменной 0(t).
Таким образом, если задача нормальна, то оптимальное по расходу ресурсов управление определяется соотношением (2.100). Отметим, что экономия ресурсов происходит в периоды, когда u0 (t) 0.
§ 2.7. Некоторые замечания по принципу максимума
Принцип максимума представляет собой набор необходимых условий локальной оптимальности. Действительно, если предположить, что u(t) - управление, переводящее начальную точку в множество S, то для всех u(t), близких в смысле нормы
|
|
u(t) u(t) |
|
|
|
sup |
|
|
|
u(t) u(t) |
|
|
|
, 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
удовлетворяется соотношение |
|
|
|
|
|
|||||||||||||||
|
|
J(u) J(u). |
|
|
|
|
|
|
|
|||||||||||
|
Полагая |
|
параметр |
|
достаточно |
малым, |
можно показать, |
что |
||||||||||||
существует неположительная постоянная |
р |
0 |
и функция p(t), при которых |
|||||||||||||||||
различные |
условия принципа максимума |
будут |
удовлетворяться |
для |
||||||||||||||||
p |
0 , p(t),u(t) |
и траектории x(t), соответствующей управлению u(t). |
|
|||||||||||||||||
62
