afanasev_v_n_optimalnye_sistemy_upravleniya_ana

Теперь вместо уравнения (8.81), определяющее оценку x(t), следует использовать уравнения (8.84) и (8.83), которые запишем в виде

В уравнение (8.81), определяющее матрицу K(t), входит дисперсионная

Для отыскания выражения d (t) воспользуемся уравнениями (8.70) и dt

(8.81). Получим

Пусть Ф(t, )- фундаментальная матрица решений дифференциального уравнения (8.87). Тогда, учитывая свойства дельта - функции, будем иметь

M[ (t)wT (t)]

t0

1 B(t) K(t)C(t)B(t) W(t), 2

153

M[ (t)sT (t)]

t

Ф(t, )M[B( )w( )sT (t) K( )s( )sT (t)]d

t0

(8.90)

1 B(t) K(t)C(t)B(t) W(t)BT (t)CT (t) 2

1 K(t)Q(t)V(t)QT (t). 2

Подставляя (8.89) и (8.90) и их транспонированные значения в (8.88), получим уравнение для дисперсионной матрицы ошибок

d P(t) dt

[A(t) K(t)C*(t)]P(t) P(t)[A(t) K(t)C*(t)]T

K(t)[Q(t)V(t)QT (t) C(t)B(t)W(t)BTCT (t)]KT (t)B(t)W(t)BT (t).

Уравнение (8.85) преобразуем, подставив в него выражение (8.82).

Начальные условия для уравнения (8.92) можно получить из

дифференциального уравнения (8.85) и уравнения (8.83), где матрица K(t) определяется соотношением (8.82). Дисперсионная матрица P(t) является решением нелинейного дифференциального уравнения (8.92) с начальными условиями (8.93).

§ 8.7. Оптимальная фильтрация нелинейных динамических систем

Большая часть из встречающихся динамических систем и систем измерений являются нелинейными. Уравнениями оптимальных фильтров, полученных в разделах 8.3 – 8.5 для линейных систем, можно пользоваться в случае нелинейных систем с «белыми» шумами, если провести линеаризацию относительно номинальной траектории или если непрерывно (или от случая к случаю) проводить линеаризацию относительно текущих

154

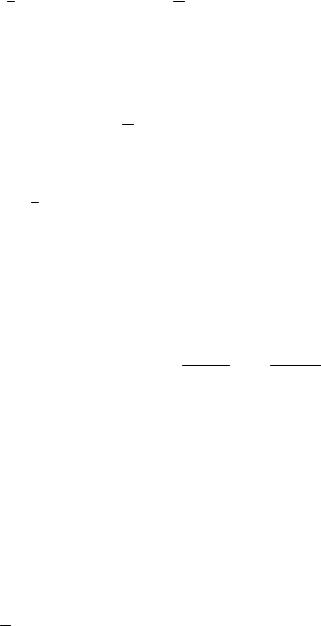
где y Rm , m n; M[v(t)] 0, M[v(t)vT ( )] V(t) (t ), M[{x(t0) x0}vT ( )] 0, M[{w(t) w(t)}vT ( )] 0.

Нелинейности через функции f (x,t) и C(t,x) входят соответственно только в уравнения (8.96) и (8.97). Одним из возможных фильтров для рассматриваемой нелинейной системы является следующая очевидная модификация линейного фильтра из § 8.3:

Здесь частные производные f (x,t) и C(x,t) могут вычисляться вдоль

x x

номинальной траектории или для большей точности их можно вычислять полагая x(t) x(t). Однако в этом случае матрицу P(t) заранее вычислить нельзя, так как она, согласно выбранной процедуре, зависит от текущей оценки x(t), следует вычислять в реальном времени.

§ 8.8. Оптимальное сглаживание и интерполяция для непрерывных процессов

Задача оптимального сглаживания для непрерывных процессов может быть поставлена как задача определения значений x(t0 ) и , которые минимизируют критерий качества

J(x0,w) 1 x(t0 ) x(t0 ) Т P 1(t0 ) x(t0 ) x(t0 ) 2

Это детерминированная задача оптимизации, к которой применимы стандартные методы оптимального управления. Гамильтониан в этой задаче имеет вид

156

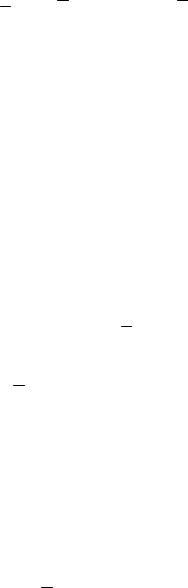
H1 w(t) w(t)W 1(t) w(t) w(t) T 2

2

T (t) A(t)x(t) B(t)w(t).

Необходимые условия минимума функционала (2.99) при ограничении (8.100) записываются как уравнения Эйлера – Лагранжа.

необходимые условия минимума функционала (8.97) будут описываться двухточечной краевой задачей

можно получить либо методами, использующими переходные матрицы, либо методом прогонки. Остановимся на последнем, положим, что решение x(t) x(t/T) может быть представлено в виде

где x(t)и P(t) подлежат определению. Дифференцируя (8.106) и учитывая

(8.104), получаем

157

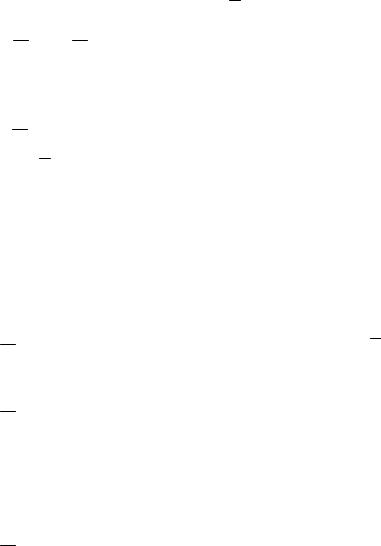
A(t)x(t) B(t)W(t)BT (t) (t) B(t)w(t)

d x(t) d P(t) (t) dt dt

P(t) CT (t)V 1(t)C(t)x(t) AT (t) (t) CT (t)V 1(t)y(t)

CT (t)V 1(t) y(t) C(t)x(t) , (T) 0,

тогда как уравнения (8.107) интегрируются «вперед». Зная (t) из формулы (8.103) можно найти w(t /T), а из формулы (8.106) − x(t/T).

158

Глава 9. Управление линейными стохастическими системами с квадратическим функционалом качества

Применение методов аналитического конструирования оптимальных управлений основано на определенных допущениях, основным из которых является выбор функционала критерия оптимума. В принципе функционал качества может быть выбран из довольно широкого класса. Однако известные решения задачи аналитического конструирования в замкнутой форме получаются только для квадратического функционала. Поэтому синтез на основе квадратических функционалов имеет широкое применение, кроме того, во многих практических задачах он соответствует их существу.

Квадратический критерий имеет еще одну замечательную особенность, допускающую возможность значительного упрощения синтеза оптимального управления в линейных системах при случайных возмущениях. Эта особенность состоит в справедливости так называемого «принципа стохастической эквивалентности» или теоремы разделения. Этот принцип позволяет применить результаты аналитического конструирования управления линейными объектами и методы построения оптимальных фильтров, так как задача аналитического конструирования управлений линейными объектами, подверженных случайным возмущениям, с квадратическим критерием качества сводится к двум последовательно решаемым задачам.

Таким образом, важным следствием теоремы разделения является возможность объединения результатов теории линейной фильтрации случайных сигналов и детерминированной теории оптимального управления при синтезе оптимальных систем.

§ 9.1. Системы с процессами типа «белого» шума

Рассмотрим задачу построения оптимального регулятора для линейной системы, возмущаемой гауссовским «белым» шумом, когда критерий качества является квадратичной формой, начальные условия случайны, но точно известно состояние системы. Представим управляемую систему следующей линейной моделью

Пусть критерий качества есть среднее по ансамблю от квадратичной формы

159

J(x,u)

где матрицы F(t) и Q(t)- положительно полуопределены, матрица R(t) - положительно определена,

время T - задано.

Требуется выбрать управление u(t), которое минимизирует функционал (9.3). Процесс w(t) представляет собой случайное возмущение с нулевым средним и малым (по сравнению с характеристическими постоянными времени системы) временем корреляции. Таким образом, предсказать w(t) при t , даже точно зная состояние для t , не представляется возможным. Поэтому, оптимальный регулятор эквивалентен детерминированному

регулятору

где S(t) определяется решением матричного дифференциального уравнения типа Риккати

Найдем уравнения, определяющие поведение оптимальной системы в среднем. Уравнение (9.1) с учетом (9.4) будет иметь вид

Определим среднее значение критерия качества, который с учетом (9.4) можно переписать в виде

160

где tr - оператор «след матрицы».

В подынтегральное выражение функционала (9.9) добавим d S(t)X(t) , dt

компенсировав вне интеграла выражением S(t0 )X(t0 ) S(T)X(T) . Принимая во внимание, что S(T) F , и, учитывая (9.6), получим

Таким образом, поскольку при неотрицательно определенных матрицах

T

S(t) и W(t) величина tr S(t)W(t)dt неотрицательна, наличие шума в системе

t0

(W(t) 0) увеличивает значение критерия качества.

Рассмотрим статистически стационарный случай. Если управляемая система и шум в ней стационарны (матрицы A, B,W постоянны), матрицы Q, R положительно определены и содержат постоянные элементы, T (F 0), то регулятор может быть стационарным, т.е. может быть постоянной матрица S . Матрица ковариаций состояния также постоянна и определяется решением алгебраического уравнения

A BR 1BT S X X A BR 1BT S T W 0.

Матрица ковариаций управления определяется

U R 1BT SX S BR 1 ,

где матрица S определяется решением алгебраического уравнения

SA AS SBR 1BT S Q 0.

161

§ 9.2. Принцип стохастической эквивалентности

Пусть для t [t0,T] задана линейная модель системы

x(t0 )- гауссовский случайный вектор с нулевым математическим ожиданием, независимый от w(t)и v(t), т.е.

Так как оптимальное управление есть функция состояния объекта, а не его измеряемых координат, то использовать функционала качества в том виде, как он записан в (9.15), не представляется возможным, так как x(t) наблюдается по условию задачи в аддитивной связи с помехой типа «белого» шума v(t).

Введем в рассмотрение оценку (t) Rn процесса x(t), построенную по измеряемому процессу y(t), и ошибку оценивания (t), определяемую выражением

162