
afanasev_v_n_optimalnye_sistemy_upravleniya_ana
.pdf
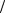 p 0( ), f (x0 ,v, )
p 0( ), f (x0 ,v, )
 p 0( ), f (x0 ,u0 , )
p 0( ), f (x0 ,u0 , ) 0.
0.
Учитывая (2.20), последнее выражение можно переписать в виде
|
|
|
|
|
|
|
(2.28) |
H(x0 ,u0 , p 0, ) H(x0 ,v, p 0, ) |
|||||||
или |
|
||||||
H(x0 ,u0 , |
|
0, ) max H(x0 ,v, |
|
0, ). |
(2.29) |
||
p |
p |
||||||
|
|
v U |
|
||||
Таким образом, если управление u0 (t) и |
траектория x0 (t) доставляют |
||||||
минимум функционалу (2.23), то существует такая непрерывная вектор-
|
|
|
|
|
|
|
функция |
|
p T (t) p0(t), p1(t),...,pn , |
удовлетворяющая уравнению (2.18) и |
|||
условию |
(2.25), что при t [t0 ,T] |
функция Понтрягина H(x0 ,u0 , |
|
0,t) (2.20) |
||
p |
||||||
достигает максимума по всем u(t) U.
В задаче со свободным правым концом и заданным временем окончания переходного процесса условия трансверсальности (2.25) приводят к такой же структуре двухточечной краевой задачи, которая рассматривалась в разделе § 1.2. Однако, если в задаче Лагранжа управление находится при помощи условия стационарности
H(x,u, ,t) 0,
u(t)
то в задаче Понтрягина управление отыскивается с помощью условия
H(x0 ,u0 , p 0, ) max H(x0 ,v, p 0, ).
v U
Естественно, что в случае, когда U совпадает со всем пространством, а функция Понтрягина имеет один экстремум, который при этом является максимумом, оба условия дают одну и ту же функцию u0 (t).
§ 2.3. Задача с фиксированными значениями некоторых переменных состояния в заданный момент окончания переходного процесса
Доказательство принципа максимума Понтрягина для рассматриваемого случая усложняется тем, что неравенство, аналогичное (2.24), должно выполняться не для всех вариаций, а только для тех из них, которые не нарушают граничных условий.
Проведем ряд дополнительных построений для общего случая, когда значения некоторых переменных фиксированы, а время окончания переходного процесса не фиксировано.
Найдем множество концевых вариаций, получающихся вследствие воздействия нескольких игольчатых вариаций управления и вариаций времени окончания переходного процесса.
Определим вначале концевую вариацию dx(T), получаемую при воздействии одной игольчатой вариации управления и варьировании времени окончания переходного процесса:
d |
|
(T) lim |
x*(T dT) x(T) |
, |
|
x |
|||||
|
|||||
|
|
0 |
|
||
|
|
|
43 |
||

где dT - произвольное положительное или отрицательное число. Учитывая, что
x*(T dT) x*(T) f (x,u,T) dT 0( ),
получим
|
|
|
x*(T) x(T) f (x,u,T)dT |
|
0( ) |
|
|||
|
|
|
|
||||||
dx(T) lim |
|
|
|
|
|
|
|||
|
|
||||||||
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
x(T) f (x,u,T)dT.
Содержательный смысл концевой вариации dx(T)такой же, как и полной вариации dx(T) из раздела § 1.4.
Рассмотрим теперь результат воздействия игольчатого варьирования на нескольких отрезках траектории, т.е. результат воздействия управления:
v |
если t [ |
|
, |
|
|
l |
|
], |
(2.30) |
|||
u*(t) |
0k , |
|
|
|
k |
|
|
k |
|
k |
k 1,...,q. |
|
u |
(t), |
если t [ k , |
k |
lk ], |
|
|||||||
Обозначим через |
|
k (t) |
вариацию фазовой траектории, получающейся |
|||||||||
x |
||||||||||||
при независимом воздействии одной игольчатой вариации uk (t). Вариация
xk (t)зависит от выбора параметров vk , k , lk , определяющих игольчатую
вариацию uk (t). Для нас будет интересна зависимость xk (t) только от lk :
xk (t) xk (t,lk ). |
(2.31) |
||
Поскольку дифференциальное уравнение (2.16), решением которого |
|||
является |
|
k (t), линейное, а в начальные условия (2.17) параметр lk |
входит |
x |
|||
как множитель, то выражение (2.31) можно переписать в виде |
|
||
xk (t) lk xk (t,1),
где xk (t,1)- вариация фазовой траектории, соответствующая игольчатому варьированию с параметрами vk , k , lk 1.
Обозначим через x суммарную вариацию, получающуюся при управлении (2.30). На основании линейности управлений (2.16) суммарная вариация x (t) равна сумме вариаций
x (t) xk t lk xk t,1 .
k 1 |
k 1 |
Полная вариация dx(T), вызванная воздействием управления (2.30) и вариацией времени окончания переходного процесса, будет иметь вид
|
|
q |
|
||||
d |
|
(T) lk |
|
k (T,1) |
|
(x0,u0 ,T)dT . |
(2.32) |
x |
x |
f |
|||||
|
|
k 1 |
|
||||
Совокупность векторов dx(T) образует множество К, которое является выпуклым конусом. (Множество К называется выпуклым конусом, если: 1) для любой точки М множества К, отличной от вершины Р, радиус РМ целиком содержится в этом множестве; 2) отрезок М1М2 , соединяющий произвольные точки М1 и М2 множества, принадлежит этому множеству). Конус К называют конусом концевых вариаций.
44

Дадим геометрическую интерпретацию множеству концевых вариаций
(2.32). В (n+1) - мерном фазовом пространстве X переменных |
x0 ,x1,...,xn |
||||
будем рассматривать множество К, состоящее из точек |
|
||||
K : |
|
(T) d |
|
(T) , |
(2.33) |
x |
x |
||||
иначе говоря, будем откладывать от концевой точки x(T) векторы концевых вариаций (2.32), получающиеся при всевозможных выборах q,vk , k ,lk , k 1,...,q, dT .
P 
n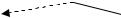 K
K
Г
x00 (T) Jmin
x1 |
x(t0 ) |
x2 |
|
|
x0 |
Рис. 2.3. Конус концевых вариаций
Покажем, что К – выпуклый конус. Если dx(T) - концевая вариация, то
и dx(T), |
0, |
является |
концевой вариацией. Чтобы убедиться в этом, |
||||||||||||
достаточно, согласно (2.32), ввести обозначения: |
|||||||||||||||
|
|
l1 l |
k |
, |
dT dT . |
|
|
|
|
|
|||||
|
|
k |
|
|
1 |
|
|
|
|
точкой x |
|
|
(T) множество К |
||
Следовательно, |
вместе с |
каждой |
(T) d |
|
|||||||||||
x |
|||||||||||||||
содержит и луч |
|
(T) d |
|
(T), 0, |
т.е. множество К имеет вершину в точке |
||||||||||
x |
x |
||||||||||||||
|
|
(T). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как точки, расположенные ниже оптимальной траектории, недостижимы, то множество К не может заполнить все пространство. Из этого следует, что К – конус.
Для того чтобы сделать заключение о выпуклости конуса К,
рассмотрим две произвольные вариации и dx2 (T), и пусть - произвольное неотрицательное число 0 1. Тогда
45
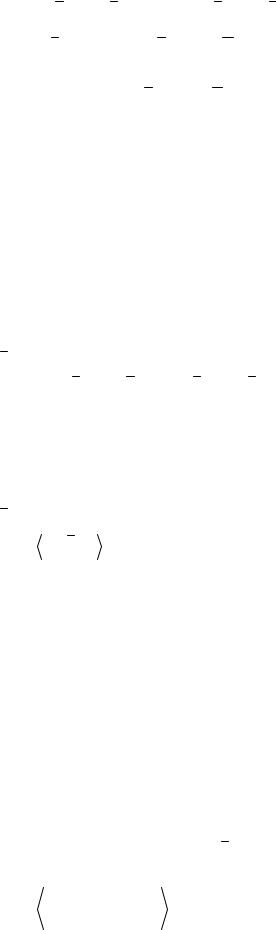
[x(T) dx1(T)] (1 )[x(T) dx2 (T)]
q1
x(T) [ lk1 xk1 (T,1) f (x0 ,u0T)dT1]
k1
q2
(1 )[ lk2 xk2 (T,1) f (x0 ,u0T)dT2 ].
k2
Обозначив
|
|
|
|
|
|
|
|
l1 |
l |
k |
, l2 (1 )l |
k |
|
, dT dT (1 )dT , |
|||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
2 |
1 |
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q1 |
|
|
|
|
|
|
|
q2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x |
(T) lk1 |
|
x |
k (T,1) lk2 |
x |
k (T,1), |
||||||||||||||||
получим |
|
|
|
|
|
|
|
k1 |
|
|
|
|
|
|
|
k2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
[ |
|
|
(T) d |
|
|
1(T)] (1 )[ |
|
(T) d |
|
2 |
(T)] |
|
|
|
|||||||||||||||||
x |
x |
x |
x |
(2.34) |
|||||||||||||||||||||||||||
|
|
|
(T) |
|
|
(T) |
|
|
(x0 ,u0 ,T)dT. |
|
|
|
|
|
|||||||||||||||||
x |
x |
f |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
Так как |
|
|
|
(T)- вершина конуса, а вид второго и третьего слагаемого |
|||||||||||||||||||||||
|
|
|
|
|
|
x |
|||||||||||||||||||||||||
(2.34) такой же, как и (2.32), |
|
то отрезок, |
соединяющий вариации d |
|
1(T) и |
||||||||||||||||||||||||||
|
x |
||||||||||||||||||||||||||||||
dx2 (T), входит в конус концевых вариаций. Иными словами, вместе с двумя
точками x(T) dx1(T)и x(T) dx2 (T) конус К содержит отрезок (2.34), соединяющий эти точки, т.е. К – выпуклый конус. Поэтому через вершину Р (рис. 2.3) можно провести гиперплоскость Г таким образом, что конус будет расположен в одном из полупространств (в общем случае возможно существование нескольких гиперплоскостей Г). Проведем теперь через точку Р «направленную вниз» нормаль n к гиперплоскости Г. Для любого вектора
dx(T) K будет справедливо |
|
n,dx(T) 0. |
(2.35) |
Используя это соотношение, выведем принцип максимума Понтрягина. Вернемся к постановке задачи. Пусть граничные условия системы
|
d |
x(t) f (x,u,t), |
x Rn , u Rr |
|
|
|
|
||
|
dt |
|
|
|
имеют вид |
|
|
||
|
x(t0 ) x0 , |
|
(2.36) |
|
i (x(T)) 0, i 1,...,k, k n, |
||||
t0 , T задано,
причем функции i (x(T)) непрерывны и непрерывно дифференцируемы, а
якобиан 
 i(x(T)/ x(T)
i(x(T)/ x(T)
 имеет свой максимальный ранг k (в этом случае
имеет свой максимальный ранг k (в этом случае
говорят, что правый конец принадлежит (n-k) - мерному гладкому многообразию).
Концевые вариации dx(T) не должны нарушать граничных условий (3.36), т.е. должно выполняться соотношение
i |
(x(T)) |
|
(2.37) |
|
|
|
, dx(T) , |
i ,...,k. |
|
|
|
|||
x(T) |
|
|
||
46

В качестве конечного значения вектор - функции |
p(T) выберем вектор |
||||
nT (n0, n1,...,nn ), т.е. |
|
||||
|
|
(T) n. |
(2.38) |
||
|
p |
||||
Поскольку вектор |
|
(T) выбран в виде (2.38), |
то для любых dx(T), |
||
p |
|||||
удовлетворяющих проварьированным граничным условиям (2.37), должно выполняться равенство
p(T),dx(T) 0. |
(2.39) |
Используя выражения (2.37) и (2.39), получим условия трансверсальности в таком виде, как это уже было получено в разделе § 1.4. Для этого умножим
каждое уравнение |
|
(2.37) |
на i , сложим полученные выражения, а затем |
|||||||||||||
результат вычтем из уравнения (2.39). Тогда получим |
|
|
||||||||||||||
n |
k |
|
|
(x(T)) |
|
|
||||||||||
pj (T) i |
|
i |
|
|
dxj (T) 0. |
(2.40) |
||||||||||
|
x (T) |
|||||||||||||||
|
i 1 |
|
|
|
|
|
||||||||||
|
|
|
j |
|
|
|
||||||||||
j 1 |
|
|
|
|
|
|
|
|||||||||
Из выражения (2.40) получаем, что |
|
|
||||||||||||||
k |
|
(x(T)) |
|
|
|
|
|
|
|
|
|
|
||||
pj (T) i |
|
|
i |
|
, j 1,...,n. |
(2.41) |
||||||||||
|
xj (T) |
|||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как, |
по |
|
предположению, якобиан |
|
|
|
i(x(T))/ x(T |
|
|
|
имеет свой |
|||||
|
|
|
|
|
||||||||||||
максимальный ранг k, то, приравнивая к нулю соответствующие k коэффициентов в (2.40), можно получить систему с ненулевым детерминантом, определяющую множители 1,..., k по i (x(T)) однозначно.
Остальные n-k условий в (2.40) равны нулю в силу независимости
оставшихся вариаций. |
|
|
|
|
|
|
|
||||||||||
|
|
В силу выбора |
|
(T) n (2.38) неравенство (2.35) можно переписать в |
|||||||||||||
p |
|||||||||||||||||
виде |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
(T), d |
|
|
(T) 0. |
|
|
|
|
|
|
(2.42) |
|||
|
|
|
p |
x |
|
|
|
|
|
|
|||||||
|
|
Поскольку в настоящем разделе рассматривается задача с |
|||||||||||||||
фиксированным временем окончания переходного процесса, |
то dT=0 и |
||||||||||||||||
d |
|
(T) |
|
(T), так что неравенство (2.42) можно переписать в виде |
|
||||||||||||
x |
x |
|
|||||||||||||||
|
|
|
|
(T), |
|
(T) 0. |
|
|
|
|
|
|
(2.43) |
||||
|
|
|
p |
x |
|
|
|
|
|
|
|||||||
|
|
Согласно (2.19) |
выражение |
|
(t), |
|
(t) const для t T . |
Этот факт |
|||||||||
|
|
p |
x |
||||||||||||||
позволяет осуществить перенос неравенства (2.43) из конечного времени t=T
в момент времени t , |
при котором |
осуществлялось игольчатое |
|||||||||||||||
варьирование: |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
(T), |
|
|
(T) |
|
( ), |
|
( ) |
0. |
(2.44) |
||||||
|
p |
x |
p |
x |
|||||||||||||
Подставляя в (2.44) выражение (2.17) для |
|
( )при x0 ( ), u0 ( ), получим |
|||||||||||||||
x |
|||||||||||||||||
неравенство |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0( ), |
|
(x0 ,v, ) |
|
|
0( ), |
|
(x0 ,u0 , ) 0, |
|
|
|
|||||
|
p |
f |
p |
f |
|
|
|
||||||||||
которое, используя функцию Понтрягина (2.20), можно переписать в виде
47

H(x0 ,v, p, ) H(x0 ,u0 , p, ),
или окончательно
|
|
|
|
|
|
H(x0 ,u0 , p, )) max H(x0 ,v, p, ) . |
(2.45) |
||||
|
|
v U |
|
||
Таким образом, если управление u0 (t) и траектория |
x0 (t) доставляют |
||||
минимум функционалу (2.23) при уравнениях связи (2.22) и краевых условиях (2.36), то существует такая ненулевая непрерывная вектор -
функция |
|
|
|
|
|
|
|
|
, |
удовлетворяющая |
условиям |
p T (t) (p |
|
, p ,...,p |
n |
), p |
|
||||||
|
|
|
|
|
|
|
|
|
|||
трансверсальности (2.41), |
что |
при |
каждом t [t0 ,T] функция |
Понтрягина |
|||||||
достигает при оптимальном управлении u0 (t)максимума по всем u(t) U . Отметим, что при свободном правом конце условия трансверсальности
(2.41) дают
pj (T) 0, j 1,...,n,
что совпадает с результатами предыдущего параграфа.
§ 2.4. Задача с фиксированными значениями некоторых переменных состояния в неопределенный момент окончания переходного процесса
Управляемый объект описывается нелинейным векторным дифференциальным уравнением вида (2.1)
|
d |
x(t) f (x,u,t), x Rn , |
,u Rr |
(2.46) |
|
|
|||
|
dt |
|
|
|
с граничными условиями |
|
|
||
|
x(t0 ) x0 , |
|
(2.47) |
|
i (x(T),T) 0, i 1,...,k, |
k n, |
|||
t0 задано.
Требуется отыскать управление u(t) U , доставляющее минимум функционалу
T |
(2.48) |
J(x,u) L(x,u,t)dt. |
|
t 0 |
|
Положив сначала dT=0 и повторяя рассуждения раздела § 2.3, получим, что необходимые условия рассматриваемой задачи содержат в себе все необходимые условия, установленные для задачи с заданными значениями некоторых переменных состояния в заданный момент окончания
переходного |
|
|
процесса |
(§ 2.3). Далее |
вернемся к |
неравенству (2.35) |
||||||||||||
n,d |
|
(T) 0. |
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Рассмотрим |
концевую вариацию |
d |
|
(T)(2.32) |
при lk 0 |
k 1,...,q |
||||||||||
|
|
x |
||||||||||||||||
(игольчатые вариации отсутствуют), и при dT 0 будем иметь |
|
|||||||||||||||||
|
|
d |
|
|
(T) |
|
|
(x0 ,u0 ,T)dT . |
|
|
|
|
(2.49) |
|||||
|
|
x |
|
f |
|
|
|
|
||||||||||
Подставляя (2.49) |
в (2.42), получим |
|
|
|
|
|
||||||||||||
|
|
|
|
(T), |
|
|
(x ,u ,T)dT |
. |
|
|
|
|
(2.50) |
|||||
|
|
|
p |
|
f |
|
|
|
|
|||||||||
48

Поскольку по условию dT может принимать как положительные, так и отрицательные значения, то соотношение (2.49) выполняется при единственном условии
|
|
|
|
(2.51) |
p(T), f (x0,u0,T) 0, |
||||
т.е. в конечный момент t=T функция Понтрягина должна быть равной нулю
|
|
|
|
H(x ,u , p,T) . |
(2.52) |
||
Таким образом, в том случае, когда рассматриваются задачи с фиксированными значениями некоторых переменных состояния в неопределенный момент времени окончания переходного процесса, к необходимым условиям, полученным в предыдущем разделе (§ 2.3), добавляется необходимое условие трансверсальности (2.52).
Для частного случая, когда объект и функционал качества не зависят в явном виде от времени t, т.е. объект описывается уравнением
d x(t) f (x,u), x Rn , u Rr dt
и функционал имеет вид
T
J(x,u) L(x,u)dt,
t0
функция Понтрягина не зависит от времени и его полная производная по t имеет вид
dH(x,u, p) |
H(x,u, p) x(t) H(x,u, p) |
p(t) |
H(x,u, p)u(t). |
||||||||
|
|
|
|
|
. |
|
|
|
. |
|
. |
dt |
|
|
(t) |
|
|
|
(t) |
|
u(t) |
||
x |
p |
|
|||||||||
Учитывая тот факт, что первые два слагаемых образуют каноническую систему, связанную с основной задачей, это выражение можно переписать:
|
dH(x,u, p) |
|
|
H(x,u, p) |
|
du(t) |
. |
|
|
|
|
|
dt |
u(t) |
|
|
|
|
|||||
|
|
|
|
dt |
|
|
|
||||
Внутри множества U необходимое условие максимума Н состоит в том, |
|||||||||||
чтобы dH(x,u, |
|
)/du(t) 0. |
Отсюда следует |
равенство dH(x,u, |
|
)/dt 0. Если |
|||||
p |
p |
||||||||||
максимум Н (минимума функционала J) |
достигается только на замыкании |
||||||||||
области допустимых управлений, то равенство H(x,u, p)/ u(t) 0 не будет выполняться. В этих случаях, как правило, u(t) является постоянным,
следовательно, и опять dH(x,u, p)/dt 0. Если одно из двух этих
условий не удовлетворяется, то можно показать, что векторы H(x,u, p)/ u(t) и du(t)/dt взаимно ортогональны и, следовательно, полная производная
dH(x,u, p)/dt 0.
Таким образом,
max H(x,u, p) 0, t [t |
0 ,T]. |
(2.53) |
||
u U |
|
|
|
|
Покажем несколько иным способом, что функция |
H(x,u, |
|
) постоянна |
|
p |
||||
на интервале [t0 ,T]. Для |
этого воспользуемся |
дополнительным |
||
|
|
49 |
||

предположением, что множество точек, в которых u0 (t) непрерывно,
обладает свойством: если t [t0 ,T]- |
точка, |
в которой u0 (t) |
- непрерывно, то |
||||||||||||||||||||
u*(t) непрерывно |
для |
всех |
|
t [t0 ,t*], |
достаточно |
близких |
к |
t . |
Это |
||||||||||||||
предположение справедливо, если u*(t) имеет конечное число разрывов. |
|
|
|
||||||||||||||||||||
Пусть t1 |
и |
|
t2 - |
элементы из |
[t0 ,T], |
причем t1 > t2 |
и |
функция |
|||||||||||||||
u0 (t)непрерывна на интервале |
[t1,t2 ]. |
Покажем, что |
функция |
H(x0 ,u0 , |
|
0) |
|||||||||||||||||
p |
|||||||||||||||||||||||
постоянна на этом интервале. Так |
как |
|
x0 , u0 , |
|
0 непрерывны |
на |
этом |
||||||||||||||||
|
p |
||||||||||||||||||||||
интервале, то множества |
|
|
] , u0 |
|
|
|
|
] |
|
|
|
|
|
|
|
||||||||
x0 (t):t [t |
,t |
2 |
] , p(t):[t ,t |
2 |
(t):[t ,t |
2 |
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
ограничены и, следовательно, имеет соответствующие |
компактные |
||||||||||||||||||||||
замыкания X1, P1,U1 . Функция H(x,u, |
|
) непрерывна на |
компактном |
||||||||||||||||||||
p |
|||||||||||||||||||||||
множестве X1, P1,U1 |
и имеет, |
в |
силу |
сделанных |
предположений, |
||||||||||||||||||
непрерывные |
частные |
производные |
по |
|
x(t), p(t)на этом |
компактном |
|||||||||||||||||
множестве. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим действительную функцию m от x(t) и p(t), приняв
|
|
|
m(x, p) supH(x,u, p). |
|
|
|
|
|
|
|
(2.54) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
u U |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Так как u0 (t)непрерывно на интервале [t1,t2 ], то из соотношения (2.45) |
||||||||||||||||||||||||||
можно заключить, что |
|
|
|
|
|
|
|
(2.55) |
|||||||||||||||||||||
|
|
|
m(x0 , p0 ) H(x0 ,u0, |
|
|
0) |
|
|
|
|
|
|
|
||||||||||||||||
|
|
p |
|
|
|
|
|
|
|
||||||||||||||||||||
для t из [t1,t2 ], и поэтому функция m(x0 , p0 ) |
непрерывна. Предположим, что t |
||||||||||||||||||||||||||||
и t* - различные точки из [t1,t2 ], тогда получим |
|||||||||||||||||||||||||||||
|
|
|
m(x0 (t*), p0 (t*)) H(x0 (t*),u0 (t), |
|
|
0(t*)), |
(2.56) |
||||||||||||||||||||||
|
|
p |
|||||||||||||||||||||||||||
и поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
m(x0 (t*), p |
0 (t*)) m(x0 (t), p0 (t)) |
(2.57) |
|||||||||||||||||||||||||||
H(x0 (t*),u0 (t), |
|
|
0(t*)) H(x0 (t),u0 (t), |
|
|
0(t)). |
|||||||||||||||||||||||
p |
|
p |
|
|
|||||||||||||||||||||||||
Если t*>t, то из неравенства (2.57) можно найти |
|||||||||||||||||||||||||||||
|
|
|
|
m(x0 (t*), p0 (t*)) |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
t* t |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
H(x0 (t*),u0 (t), |
|
0(t*)) H(x0 (t),u0 (t), |
|
0(t)) |
||||||||||||||||||||
|
|
|
|
p |
p |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t* t |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||
Так как производные x 0(t), |
p 0(t) существуют и H / x, H / p непрерывны, то |
||||||||||||||||||||||||||||
при t* t |
|
справа получается соотношение |
|
|
|||||||||||||||||||||||||
|
d |
m[x0 (s), p0 (s)]t |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.58) |
|||||
|
|
H(x,u, p) . |
H(x,u, p) . |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x(t) |
|
|
|
|
|
|
|
|
p(t) 0 |
|
|
||||||||||
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
p(t) |
|
|
|
|
|
|
|
|
|
||||||||||||
(так как |
x0 (t), p0 (t) удовлетворяют каноническим уравнениям). Аналогично |
||||||||||||||||||||||||||||
при t* t |
|
слева имеем |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
50

d m[x0 (s), p0 (s)]t ds
(2.59)
H(x,u, p) x. (t) H(x,u, p) p. (t) 0.
x(t) p(t)
Поскольку H / x, H / pнепрерывны на X1 P1 U1 и x0 (t), p0 (t) существуют, то существуют и производные от m[x0 (t), p0 (t)], и на основании выражений (2.58) и (2.59) можно заключить, что
|
d |
m[x0 (s), p0 (s)] 0. |
|
(2.60) |
||||
|
|
|
||||||
|
ds |
|
|
|||||
С помощью соотношений |
|
|
||||||
|
H(x (T),u (T), |
|
(T)) |
|
||||
|
p |
|
||||||
и (3.55) найдем |
|
(2.61) |
||||||
|
H(x (t),u (t), |
|
(t)) , |
t [t ,T]. |
||||
|
p |
|||||||
Таким образом, если управление u0 (t) и траектория |
x0 (t) доставляют |
|||||||
минимум функционалу (2.48) при уравнениях связи (2.46), ограничениях на
управление |
u(t) U и краевых условиях |
(3.47), |
то существует |
такая |
||
непрерывная |
ненулевая |
функция |
|
T (t) |
p0(t), p1(t),...,pn (t) , |
p0 0, |
p |
||||||
удовлетворяющая сопряженной системе (3.18) и условиям трансверсальности (2.40) и (2.52), что при каждом функция Понтрягина достигает максимума при оптимальном управлении u0 (t) U.
Для частного случая, когда объект и функционал качества не зависят в явном виде от времени, максимальное значение функции Понтрягина, принимаемое на оптимальной траектории, постоянно и равно нулю.
Рассмотрим случай, когда ограничения на правом конце задаются в виде функций, т.е. в момент окончания переходного процесса состояние системы должно отвечать следующему условию:
i(x(T),T) 0, i ,...,k, k n 1. (2.62)
Вывод необходимых условий проведем с помощью редукции этой задачи к задаче, уже рассмотренной выше.
Введем обозначение xn 1(t) t
и рассмотрим систему
|
d |
|
|
(t) |
|
(x,u,xn 1), |
d |
xn 1(t) 1, |
|
|
|||||||||||
|
|
x |
f |
|
|
||||||||||||||||
|
dt |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
(2.63) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
d |
|
|
(t) |
f (x |
,u,xn 1) |
|
|
(t), |
d |
pn 1(t) pi (t) |
fi (x,u,xn 1) |
. |
||||||||
|
p |
p |
|||||||||||||||||||
|
dt |
|
|
|
dt |
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
x(t) |
|
|
|
|
|
j 1 |
xn 1 |
|||||
Условия на правом конце перепишем в виде |
|
|
|||||||||||||||||||
i (x(T),xn 1(T)) 0, |
i 1,...,k. |
|
|
|
|||||||||||||||||
В такой формулировке эта задача, с одной стороны, эквивалентна задаче уже рассмотренной выше, а с другой, является частным случаем задачи § 2.3 (частным - в силу того, что время окончания переходного
51

процесса в явном виде не задано). Определим функцию Понтрягина для рассматриваемой задачи в виде
HH(x,u, p,xn 1) pn 1
ивыпишем необходимые условия оптимальности. Согласно (2.45) имеем
H(x0 ,u0 , |
|
, 0 xn 1) pn 1 |
|
|
|
|
||||||||||||
p |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
(2.64) |
|||||
max[H(x0 ,u0 , p, 0 xn 1) pn 1]. |
|
|
|
|
||||||||||||||
u U |
|
|
|
|
|
|
|
|
|
|||||||||
Поскольку pn 1( ) |
не зависит от управления, то |
выражение (2.64) |
после |
|||||||||||||||
обратной замены t xn 1 запишется в форме (2.45). |
|
|
||||||||||||||||
Условия трансверсальности (2.40) и (2.52) дают |
|
|||||||||||||||||
H(x0 ,u0 , |
|
|
, 0 xn 1) pn 1 0, |
|
|
|||||||||||||
p |
|
|
||||||||||||||||
pn 1(T) H(x0 ,u0 , |
|
0 ), |
|
|
(2.65) |
|||||||||||||
p |
|
|
||||||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|||||||
pj (T) j |
i (x(T),T) |
, |
j 1,...,n, |
(2.66) |
||||||||||||||
|
|
|||||||||||||||||
|
|
i 1 |
xj (T) |
|
|
|
|
|||||||||||
|
|
|
|
|
k |
i (x(T),T) |
|
|
|
|
||||||||
pn 1(T) j |
. |
|
(2.67) |
|||||||||||||||
T |
||||||||||||||||||
|
|
|
|
i 1 |
|
|
|
|
||||||||||
Сравнивая (2.65) и (2.67), можно записать |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|||||
H(x0 ,u0 , |
|
0,T) j |
i (x(T),T) |
. |
Таким образом, |
если |
||||||||||||
p |
||||||||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
i 1 |
xj (T) |
|
|
||||||
управление u0 (t) и траектория x0 (t) доставляют минимум функционалу (2.48) при уравнениях связи (2.46), ограничениях на управление u(t) U и краевых
условиях (2.62), то существует |
такая непрерывная ненулевая |
функция |
||
|
|
T (t) p0(t), p1(t),...,pn (t) , p0 0, |
удовлетворяющая сопряженной |
системе |
|
p |
|||
(2.18) и условиям трансверсальности (2.66) и (2.67), что при каждом t [t0 ,T] функция Понтрягина достигает максимума при оптимальном управлении u0 (t) U.
§ 2.5. Задача об оптимальном быстродействии
Сформулируем задачу об оптимальном быстродействии для подвижной области St. Дана система
|
|
|
|
|
|
d |
x(t) f (x(t),t) B(x(t),t)u(t), x Rn , u Rr . |
|
|
(2.68) |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
|
|
Предположим: |
|
|
j 1,...,r - элементы |
матриц |
f |
и |
B |
||||||||||
|
|
|
fi (x(t),t), |
bi j |
(x(t),t), i 1,...,n, |
||||||||||||||||
соответственно непрерывны относительно x(t) и t ; |
|
|
|
|
|||||||||||||||||
|
|
|
f |
|
(x(t),t) |
|
f |
(x(t),t) |
bi j (x(t),t) |
bi j (x(t),t) |
по x(t) |
|
t |
|
|||||||
2) |
|
i |
|
|
|
|
, |
|
i |
|
|
, |
|
, |
|
непрерывны |
и |
для |
|||
|
xk (t) |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
t |
xk (t) |
t |
|
|
|
|
|||||||||
i, |
k 1,...,n, |
j 1,...,r . |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
Предположим, что компоненты вектора управления u(t) u1(t),...,ur (t) |
||||||||||||||||
ограничены по величине соотношением |
|
|
|
|
|||||||||||||||||
|
uj (t) |
|
1, j 1,...,r |
для любого t или u(t) U . |
|
|
(2.69) |
||||||||||||||
|
|
|
|
||||||||||||||||||
52
