18. Рекуррентный метод наименьших квадратов

Пусть по N наблюдениям вычислен вектор коэффициентов

B_N= (X^TX)^-1X^TY=P_NX^TY

где P_N= (X^TX)^-1, и пусть в момент t_N+1получена еще одна серия отсчетов

y_N+1, x_N+1,1, x_N+1,2, ..., x_N+1,k.

Необходимо найти способ откорректировать вектор B_Nпо информации, полученной на (N+1)-ом шаге, т.е. найти способ вычисления по формуле

B_N+1=B_N+ f(y_N+1, x_N+1,j), j = 1, 2, ..., k.

В этом состоит рекуррентный МНК. Для коррекции вектора B_Nне требуется ни обращения матриц, ни повторного формирования и решения нормальных уравнений. Метод может использоваться как при оперативной, так и при ретроспективной идентификации.

Пусть

Сформируем клеточные (или блочные) матрицы

Тогда

Воспользуемся далее формулой из леммы об обращении матриц (см. Современные методы идентификации систем. Под ред. П. Эйкхоффа. М.: Мир, 1983, стр. 391).

Лемма. Если необходимые обратные матрицы существуют, тогда

(A + BCD)^1 = A^1  A^1B(C^1 + DA^1B) ^1DA^1

Доказательство.

Если лемма справедлива, то по определению обратных матриц произведение исходной матрицы A+BCDна ее обратную должно дать единичную матрицуI:

(A + BCD)[ A^1  A^1B(C^1 + DA^1B) ^1DA^1] = AA^1 + BCDA^1 

 AA^1B(C^1 + DA^1B) ^1DA^1  BCDA^1B(C^1 + DA^1B) ^1DA^1 = I +

+ BCDA^1  B(C^1 + DA^1B) ^1DA^1  BCDA^1B(C^1 + DA^1B) ^1DA^1 =

= I+ BCDA^1  BC[C^1(C^1 + DA^1B) ^1 + DA^1B(C^1 + DA^1B) ^1]DA^1 =

= I + BCDA^1  BC[(C^1 + DA^1B)(C^1 + DA^1B) ^1]DA^1 =

= I + BCDA^1  BCDA^1 = I, ч.т.д.

Пусть теперь C= 1,B=b– матрица-столбец,D=b^T, тогда можно записать

Применяя последнее выражение, когда A=X^TX;b=x, получим:

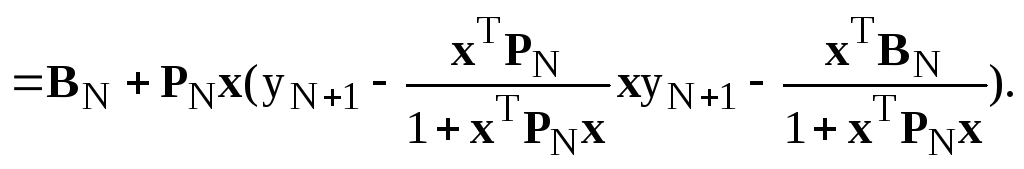Отсюда:

Т.о. для вычисления B_N+1необходимо знатьB_N;P_Nи новую информацию y_N+1;x. Вычисления состоят только в умножении и сложении матриц, т.е. отсутствуют операции обращения или решения системы уравнений.

Обратим внимание на то, что произведение

равно значению выходного сигнала, предсказываемое моделью (построенной за N шагов) по вектору новых значений x. Если это предсказываемое значение равно измеренному значению выхода, т.е. если

x^TB_N= y_N+1,

то B_N+1=B_Nи никакого пересчета вектораB_Nне требуется.

Для применения формулы пересчета вектора B_N+1на следующем (N+2)-ом шаге потребуется, очевидно, матрицаP_N+1. Эту матрицу можно получить коррекцией матрицыP_N.

Так как B_N=P_NX^TY, то выражение

B_N+1= (X^TX+xx^T)^-1(X^TY +xy_N+1)

можно записать как

B_N+1=P_N+1(X^TY+xy_N+1),

где

Последнее выражение, полученное с помощью леммы об обращении матриц, позволяет получить откорректированную матрицу P_N.

19. Взвешенный мнк и другие разновидности мнк

Взвешенный МНК применяется, когда различным ошибкам _iпридается различный вес или за счет старения результатов измерения от t₁к t_Nили за счет неодинаковой точности измерений.

Метод состоит в использовании критерия вида:

где диагональная матрица весов.

Возможные принципы назначения весов:

1. Первым измерениям (наблюдениям) назначаются меньшие веса, последним большие (учет старения информации) при условии 0 q_i1.

2. Веса назначаются как величины пропорциональные обратной величине погрешности измерений:

или

где _iинструментальная погрешность;_iсреднеквадратичная погрешность измерений; kкоэффициент пропорциональности.

Существуют и другие разновидности МНК

Если в модели со многими входами

(*)

вместо x_j(t_i) взять сигнал одного (например, первого) входа в разных степенях, то можно построить методом МНК одномерную нелинейную модель

Подставляя в модель (*) вместо x_j(t_i) различные комбинации

x₁(t_i)^p x₂(t_i)^q ... x_j(t_i)^r ...,

можно строить МНК многомерные нелинейные модели.

В модели (*) вместо x_j(t_i) можно использовать различные функции от входных отсчетов x_j(t_i). Очень часто в этом случае используются системы ортогональных функций.