19. Методы получения доброкачественных оценок. Метод максимального правдоподобия.

Оценка с помощью доверительных интервалов является более совершенным способом, чем точечная оценка. При уравнивании геодезических сетей строят доверительные интервалы для истинных значений уравниваемых величин, их функ­ций и для дисперсий (или средних квадратических отклонений) резуль­ татов измерений и их функций. Доверительные интер­валы имеет смысл строить, если измерения подчиняются нормальному закону распределения и не содержат систематических ошибок (кроме того случая, когда последние входят в уравнивание как неизвестные). Доверительный интервал для истинного значения F любой функ­ции F уравненных измерений строят в виде 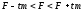,где коэффициент t выбирают из таблиц распределения Стьюдента по доверительной вероятности β и числу степеней свободы г = n-k, а средняя квадратическая ошибка 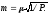В частном случае для истинного значенияX уравненного параметрическим способом неизвестного будем иметь интервал

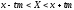,где

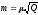
Метод максимального правдоподобия- это общий метод оценивания параметров генеральной совокупности с помощью максимизации функции правдоподобия L выборки.   Функция правдоподобия L есть совместное распределение выборки, которое представляет собой функцию параметра .

 - вектор неизвестных параметров модели.Если выборка имеет непрерывное распределение, функция правдоподобия L описывается совместной плотностью распределения 

В случае, если элементы выборки имеют дискретное распределение, функция правдоподобия принимает вид

Величину можно считать мерой правдоподобия значения θ при заданной реализацииx.

Пусть L - функция правдоподобия выборки; при наблюдаемых значениях - является функцией параметров θ. 

 Тогда оценками максимального правдоподобия θ  называются наиболее правдоподобные значения максимизирующие функциюL.

 = .Очевидно, оценки зависят от наблюдений В широких предположениях эти оценки являются оптимальными.

Часто проще искать точку максимума функции , которая совпадает св силу монотонности логарифма.Пусть- это элемент пространстваЕслиоткрытый интервал, адифференцируема и достигает максимума нато оценки максимального правдоподобия удовлетворяют уравнению

20. Равномерный закон распределения случайных величин

Во многих практических задачах приходится сталкиваться с определенными законами распределения непрерывных случайных величин. Часто встречаются законы равномерного, нормального, показательного распределения вероятностей.

Случайная величина Х называется равномерно распределенной на отрезке [a, b], если ее плотность распределения вероятностей имеет вид:

.

 

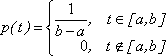График функции распределения F(x) равномерно распределенной случайной величины Х изображен на рис. 6.10.

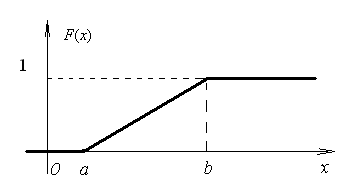
Рис. 6.10

 

Математическое ожидание равномерно распределенной случайной величины Х равно:

.

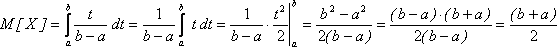По формуле (6.8) находим дисперсию равномерно распределенной величины Х:

Отсюда среднее квадратическое отклонение:

σ = =

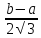
21. Биномиальный закон распределения

Биномиальный закон распределения описывает вероятность наступления события А m раз в n независимых испытаниях, при условии, что вероятность р наступления события А в каждом испытании постоянна.

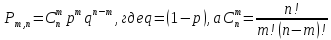
Приведённая формула иногда называется формулой Бернулли. Математическое ожидание и дисперсия для этого распределения имеют вид: 

M(X)=n*p

D(X)=n*p*q

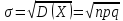
При больших n, в силу теоремы Лапласа Б.р., близко к нормальному распределению. При небольших n приходится пользоваться таблицами Б.р.