48. Второй центральный смешанный момент (ковариация).

Основной величиной для получения характеристики тес ноты связи между векторами х и у является второй смешанный центральный момент К_xy, или ковариация cov(x, y)

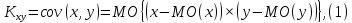
или его вычисленный выборочный вариант

Здесь v_x и v_y – центрированные величины. Ковариация в качестве меры тесноты связи не удобна, так как изменяется от –  до + и имеет разные масштабы векторов, равные их оценкам стандартного отклонения. Если привести масштабы векторов к одинаковым единичным значениям мы получим весьма удобную характеристику тесноты связи, названную парным коэффциентом корреляции r_xy

Здесь 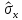и– оценки стандартного отклонения для векторов х и у. Коэффициент изменяется в пределах от – 1 до + 1. При описании процесса более чем двумя векторами измерений, парные коэффициенты находятся между всеми возможными парами векторов.

49. Парные, частные и множественные коэффициенты корреляции

Парные коэффициенты корреляции. Для измерения тесноты связи между двумя из рассматриваемых переменных (без учета их взаимодействия с другими переменными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретации аналогичны линейному коэффициенту корреляции в случае однофакторной связи.

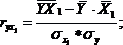
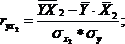
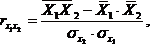
где - среднее квадратическое отклонение факторного признака;

      - среднее квадратическое отклонение результативного признака.

Коэффициент частной корреляции измеряет тесноту линейной связи между отдельным фактором и результатом при устранении воздействия прочих факторов модели.

Для расчета частных коэффициентов корреляции мо­гут быть использованы парные коэффициенты корреляции.

Для случая зависимости Y от двух факторов можно вычислить 2 коэффициента частной корреляции:

   

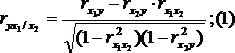
(2-ой фактор  фиксирован);

 

    

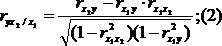
(1-ый фактор  фиксирован).

 

Это коэффициенты частной корреляции 1-ого порядка (порядок определяется числом факторов, влияние которых на результат устраняется).

Частные коэффициенты корреляции, рассчитанные по таким формулам изменяются от -1 до +1. Они используют­ся не только для ранжирования факторов модели по степени влияния на результат, но и также для отсева факторов. При малых значениях  нет смысла вводить в уравнение m-ый фактор, т.к. качество уравнения регрессии при его введении возрастет незначительно (т.е. теоретиче­ский коэффициент детерминации увеличится незначитель­но).

Коэффициент множественной корреляции (R) характеризует тесноту связи между результативным показателем и набором фактор­ных показателей:

где σ² — общая дисперсия эмпирического ряда, характеризующая общую вариацию результативного показателя (у) за счет факторов;

σ_ост² — остаточная дисперсия в ряду у, отражающая влияния всех факто­ров, кроме х;

у —   среднее значение результативного показателя, вычисленное по ис­ходным наблюдениям;

s —    среднее значение результативного показателя, вычисленное по уравнению регрессии.

Коэффициент множественной корреляции принимает только поло­жительные значения в пределах от 0 до 1. Чем ближе значение коэффи­циента к 1, тем больше теснота связи.