37.Полиномиальные преобразования при помощи функции нескольких переменных

В самом общем виде степенной полином от нескольких переменных можно записать формулой

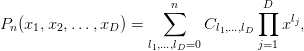
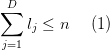
То есть в полином входят все одночлены, в которых сумма степеней переменных не превышает порядка полинома . Рассмотрим алгоритмы вычисления такого полинома, а также получения массива значений отдельных одночленов, входящих такой полином.

Каждый одночлен порядка k может быть вычислен по одному из одночленов порядка k-1 с помощью только одного умножения. Например, одночлены первого порядка получаются домножением одночлена нулевого порядка (единицы) на одну из переменных. Домножив снова каждый из этих одночленов на одну из переменных, получим все возможные одночлены второго порядка и т.д. Одночлены k-1-го порядка

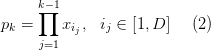
множим на одну из переменных и получаем одночлены k-го порядка.

38 . Оценка точности в методе наименьших квадратов.

Устройство оценки по методу наименьших квадратовпринадлежит к более общему классу устройств оценки с предсказанием ошибок, которые интенсивно изучались в работах по идентификации систем. Теория устройств оценки с предсказанием ошибок имеет много приложений в анализе адаптивных фильтров.

Здесь мы рассматриваем один специфический результат, связанный с асимптотической  точностью таких устройств оценки. теорему можно сформулировать следующим образом:

Теорема. При нежестких условиях стационарности и регулярности для устройства оценки по методу наименьших квадратовхарактерно асимптотическинормальное распределение, так что мы имеем:

     

где

          

- дисперсияошибки предсказания),

 определяется из, а - ковариационнаяматрицаданных. Из этой теоремы следует, что для достаточно больших значенийковариационная матрица вектора ошибки оценивания параметров

                  

приблизительно задается выражением:

  

Следовательно, эта теорема служит полезным критерием точности для устройства оценивания, основанного на протяженных последовательностях данных [под точностью мы здесь понимаем отклонение от его предельного значения]. Для коротких последовательностей данных ковариацияможет быть значительно больше, чем предсказанная формулой (3.42). таким образом, можно рассматривать матрицу, как нижнюю границудисперсииошибки оценивания.

 

39. Понятие веса. Классическая обработка неравноточных измерений

Вес:

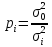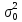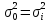; т. е. вес — величина, обратно пропорциональная дисперсии. Веса — величины относительные. О весе имеет смысл говорить, когда число измерений n > 1. Приняв p_i = 1, устанавливаем смысл . Так как при этом, то 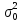есть дисперсия измерения, вес которого принят за единицу (сокращенно — дисперсия единицы веса). Измерение с весомр = 1 может быть как реально существующим, так и фиктивным.

В случае, когда дисперсии 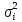неизвестны, вес вычисляют по приближенной формуле:p_i = 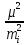, где m — СКО измерения, а величина μ, введенная вместо ϭ₀, — ошибка единицы веса. Для применения формулы ошибка m_i должна быть определена надежно (получена из результатов измерений, число которых n > 8), а также свободна от систематического влияния.

Обработка:

Вычисления при обработке ряда неравноточных измерений выполняются в следующем порядке.

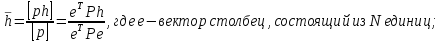
1. Наилучшей оценкой математического ожидания для неравноточных измерений является среднее взвешенное или общая арифметическая середина, которую можно вычислить по формуле: значением весов измерений на диагонали.

2. СКП единицы веса по формуле Бесселя:

3. Величина h̄ определяется с точностью:

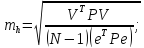
4. Нижняя граница истинного значения h = h̄ - tm_h

Верхняя граница h = h̄ + tm_h

5. Нижняя граница истинного значения 𝜇ист (СКП единицы веса) может быть найдена как 𝑚_{𝜇,𝑚𝑖𝑛}=𝑣₁∙𝜇

Верхняя граница 𝑚_{𝜇,𝑚𝑎𝑥}=𝑣₂∙𝜇

6. Нижняя граница истинного значения 𝑚ℎ2,ист (СКП средневзвешенного) может быть найдена как 𝑚_{ℎ𝑚𝑖𝑛}=𝑣₁∙𝑚_ℎ

Верхняя граница 𝑚_{ℎ𝑚𝑎𝑥}=𝑣₂∙𝑚_ℎ