8.Формула полной вероятности. Формула Бейеса

Если событие А может произойти только при выполнении одного из событи, которые образуютполную группу несовместных событий, то вероятность события А вычисляется по формуле.Эта формула называетсяформулой полной вероятности.

Вновь рассмотрим полную группу несовместных событий , вероятности появления которых. СобытиеА может произойти только вместе с каким-либо из событий , которые будем называтьгипотезами. Тогда по формуле полной вероятности

Если событие А произошло, то это может изменить вероятности гипотез .

По теореме умножения вероятностей

,откуда.Аналогично, для остальных гипотез

Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез называютсяапостериорными вероятностями, тогда как -априорными вероятностями.

9. Формула Бернулли. Примеры использования.

При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;

2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события АА в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события АА в единичном испытании буквой рр, т.е. p=P(A)p=P(A), а вероятность противоположного события (событие АА не наступило) - буквой q=P(A¯¯¯¯)=1−pq=P(A¯)=1−p.

Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли

Pn(k)=Ckn⋅pk⋅qn−k,q=1−p.Pn(k)=Cnk⋅pk⋅qn−k,q=1−p.

Распределение числа успехов (появлений события) носит название биномиального распределения.

10.Дискретные и непрерывные случайные величины и их характеристики.

Одним из основных в теории вероятностей является понятие случайной величины. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от многих случайных причин, которые заранее не могут быть учтены. Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Основными характеристиками ДСВ являются математическое ожидание, дисперсия и среднеквадратическое отклонение. Характеристикой среднего значения случайной величины служит математическое ожидание. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: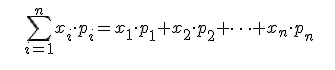

Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:Дисперсию удобно вычислять по формуле:

.

Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии:

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно. Помимо функции распределения для непрерывных случайных величин, существует еще один удобный способ задания закона распределения - плотность вероятности. Пусть функция распределения F(x)  данной НСВ Х непрерывна и дифференцируема всюду, кроме, может быть, отдельных точек. Тогда производная  f(x)  ее функции распределения называется плотностью распределения непрерывной СВ Х (или "плотностью вероятности", или просто "плотностью"): Числовые характеристики НСВ:Математическое ожидание непрерывной случайной величины Х с плотностью вероятности f(x) находится по формуле: При этом математическое ожидание существует, если интеграл в правой части формулы абсолютно сходится: это значит, что сходится интеграл Дисперсия непрерывной случайной величины Х с плотностью вероятности f(x) находится по формуле

или

Средним квадратическим отклонением случайной величины Х называется число ,определяемое равенством.Величинанеотрицательна и имеет ту же размерность, что и СВ Х.

11.Законы распределения случайных величин Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно.  Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отдельные друг от друга значения, которые можно перенумеровать. Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь разные формы. Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные (различные) значения этой случайной величины х1, х2, ..., хn с соответствующими им вероятностями р1, р2, ..., рn: хi    x1 x2 ...  xn pi    p1  p2      pn  38. Оценка точности – это центральный вопрос в любых вычислениях. СКП искомых параметров ( j mx ) вычисляется по формуле: mx Qjj j = μ (10) где μ - ошибка единицы веса. [ ] n k pv − = 2 μ Сумма [ ] 2 pv в данном случае вычисляется на последнем этапе решения задачи, при вычислении i v по найденным X j