28. Гамма распределение

29. Мешающие параметры, необходимость их выявления. Критерии Аббе и Граббса

Критерий Аббе-Линника предназначен для проверки гипотезы о том, что все выборочные значения принадлежат одной генеральной совокупности с постоянным средним против альтернативы тренда. Пусть — ряд значений взаимно независимых нормально распределенных случайных величин с математическими ожиданиямисоответственно и одинаковыми (но неизвестными) дисперсиями. Проверяется гипотеза о том, что все выборочные значения принадлежат одной генеральной совокупности со средним:

против альтернативы тренда:

Статистика критерия Аббе-Линника имеет вид

, где 

Если , то нулевая гипотеза случайности рядаотклоняется с доверительной вероятностью(критические значенияприведены в таблице). Присправелива аппроксимация, основанная на том, что случайная величина

имеет стандартное нормальное распределение. Поэтому нулевая гипотеза отклоняется, если .

Критерий Граббса

Обработку засорений производят по следующему плану:

1. Распознавание ошибок и данных;

2. Выбор метода и проведение робастного оценивания данных;

3. Критериальная и логическая проверка и интерпретация результатов устойчивого оценивания.

Простым способом для обнаружения грубых ошибок является Т – Критерия Граббса:

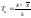
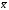- среднее значение. Оценка выборочной средней находится по истинным данным либо

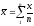
s – Выборочное среднеквадратическое отклонение случайной величины. Полученные значения 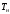сравнивают с табличными значениями процентных точек критерия Смирнова Граббса (см. приложение А). Если>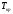, то проверяемое значение является грубой ошибкой и относится к классу выбросов. Критерий Граббса имеет некоторые недостатки. Он не точен, и не чувствителен к засорениям когда ошибки группируются на расстоянии от общей совокупности. По сравнению с оценками Граббса оценками грубых ошибок признаютсяL- и E- критерии, предложенные американскими статистиками Г. Тритьеном. И Г.Муром.

1. L-Критерий. Применяется для вычисления грубых ошибок в верхней части ранжированного ряда данных:

,

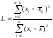2. - критерий применяется для грубых ошибок в данных, расположенных в нижней части ранжированного ряда данных:

,

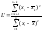3. E-критерий используется, когда в выборке имеются предположительно грубые ошибки с наибольшими и наименьшими значениями, т.е. расположенные в верхней и в нижней части ранжированного ряда данных:

,

Мешающие параметры, необходимость их выявления

Часта возникают ситуации ,когда в результате весьма вероятно наличие значимых систематических влияний , или грубых измерений , а о законе распределения погрешностей нет ни какого представления и таким образом , параметрические методы их выявления использовать нельзя .здесь можно использовать следующие подходы - 1. Выявить общую тенденцию увел.(умен)значений результатов измерения Хi в зависимости от номера i .

Xi=a*i+b

30. Приближённые методы исследования ряда случайных величин на соответствие закону распределения.

Приближенные критерии исследования ряда погрешностей на соответствие нормальному закону распределения используют сравнение некоторых известных теоретических характеристик нормального закона и их вычисленного по результатам измерений аналога. Степень отличия теоретических величин от практически вычисленных и говорит о степени приближения исследуемого ряда к нормальному закону, но только со стороны исследуемой характеристики, а не в целом.

Кроме наиболее распространенной средней квадратической погрешности т используют средние абсолютные v и вероятные (срединные) ошибки r, которые являются оценками теоретических абсолютных центральных моментов первого порядка и 0.5 (или 2) – квантили закона распределения Гаусса соответственно. Между тремя ошибками т, v и r для нормального закона распределения величин имеются теоретически строгие соотношения

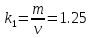
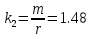
(1) k1,k2,k3-система

По величине отклонения вычисленных значений от их теоретических аналогов можно судить о степени приближения ряда к закону Гаусса, а также возможно использовать (1) для вычисления любых других двух погрешностей, если известна одна из трех. В качестве меры значимости отличия вычисленной величины от ее теоретического значения можно использовать, например, "критерий ничтожных влияний", гласящий, что величина считается неизменной, если ее вариация составляет не более 11 % от самой величины.

Для вычисления средней абсолютной ошибки пользуются формулами

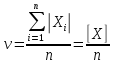
При этом первая формула используется, если ошибки Xi – истинные и оценка математического ожидания равна нулю.

Чтобы определить вероятную ошибку, величины располагают в так называемый абсолютный вариационный ряд. Если в ряде будет нечетное число элементов, то искомая ошибка будет равна значению величины, находящейся точно в середине. Если число исследуемых величин четное, то значение ошибки находится как среднее арифметическое из двух чисел, стоящих в середине ряда.

К дополнительным характеристикам распределения случайных величин, составляющих статистическую совокупность, называемым характеристиками формы, относят эксцесс Е – меру "крутости" и асимметрию А – меру "скошенности", которые получаются с использованием моментов более высокого порядка. При этом следует помнить, что для нормального закона распределения теоретические значения асимметрии и эксцесса равны нулю. Тогда значения эксцесса и асимметрии можно считать несущественными при условии

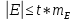
где оценки значений асимметрии и эксцесса получены по формулам

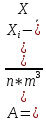
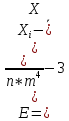
Значение вероятностного коэффициента t в (11) выбирают в зависимости от вероятности изменяя её как (1+ β)/2, так как интервал двухсторонний и используя таблицы нормального распределения. Для наиболее часто используемой вероятности 0.95 коэффициент для двухстороннего интервала будет равен 1.96.

Эмпирические значения средних квадратических погрешностей дополнительных характеристик распределения могут быть вычислены по сокращенным формулам

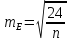
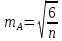
Следует иметь ввиду, что если при вычислении асимметрии А её значение окажется больше нуля, то кривая эмпирического распределения будет скошена влево, а когда А < 0 – то вправо. При величине эксцесса Е > 0 эмпирическое распределение "высоковершинное" (т.е. его вершина выше вершины теоретической кривой нормального распределения). В противном случае (Е < 0) распределение "низковершинное".

Вычисления оценок параметров нормального распределения исследуемого ряда величин (среднего арифметического и средней квадратической погрешности), а также ее дополнительных характеристик (коэффициентов k, асимметрии и эксцесса) позволяют сделать только предварительное заключение о соответствии эмпирического распределения теоретическому нормальному закону Гаусса и только по близости соответствующих теоретических характеристик распределения их вычисленным аналогам.