5. Основные формулы комбинаторики. Примеры использования

Перестановки. Пусть имеется n различных объектов.  Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно Pn=n!=1⋅2⋅3⋅...⋅(n−1)⋅n

Символ n! называется факториалом и обозначает произведение всех целых чисел от 1до n. По определению, считают, что 0!=1, 1!=0

С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов - уже 3628800 (больше 3 миллионов!).

Размещения. Пусть имеется n различных объектов.  Будем выбирать из них m объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по m, а их число равно

A^m_n =n!/(n−m)!=n⋅(n−1)⋅...⋅(n−m+1)

Сочетания. Пусть имеется n различных объектов.  Будем выбирать из них m объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по m, а их число равно

C^m_n =n!/(n−m)!⋅m!

Ясно, что сочетаний всегда меньше чем размещений (так как при размещениях порядок важен, а для сочетаний - нет), причем именно в m!m! раз, то есть верна формула связи:

A^m_n =C^m_n⋅P_m

6. Теорема сложения вероятностей и ее следствия

Теорема сложения вероятностей формулируется следующим образом.

Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:

.      (3.2.1)Доказательства для схемы случаев. Пусть возможные исходы опыта сводятся к совокупности случаев, которые мы для наглядности изобразим в виде n точек:

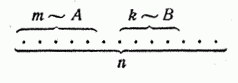
Предположим, что из этих случаев  благоприятны событию, а – событию. Тогда

Так как события  и несовместимы, то нет таких случаев, которые благоприятны и, и вместе. Следовательно, событию  благоприятны  случаев и

Подставляя полученные выражения в формулу (3.2.1), получим тождество. Теорема доказана.

Теорема на случай трех событий. Обозначая событие  буквой , и присоединяя к сумме еще одно событие , доказываем, что

методом полной индукции обобщаем теорему сложения на произвольное число несовместных событий. Предположим, что она справедлива для n событий:

и докажем, что она будет справедлива для  событий:

Обозначим:

Имеем:

.

Но т.к. для n событий мы считаем теорему уже доказанной, то

,

,что и требовалось доказать.

Таким образом, теорема сложения вероятностей применима к любому числу несовместных событий и имеет вид:

.                   (3.2.2)Следствие 1. Если события  образуют полную группу несовместных событий, то сумма их вероятностей равна единице:

.Доказательство. Так как события  образуют полную группу, то появление хотя бы одного из них – достоверное событие:

.Так как  - несовместные события, то к ним применима теорема сложения вероятностей

,откуда

,что и требовалось доказать.

Следствие 2. Сумма вероятностей противоположных событий равна единице:

.Это следствие есть частный случай следствия 1.

7.теорема умножения вероятностей . условная вероятность .Следствия из теоремы. Вероятность произведения двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.

Событие называетсянезависимым от события , если вероятность событияне зависит от того, произошло событиеили нет. Событиеназываетсязависимым от события , если вероятность событияменяется в зависимости от того, произошло событиеили нет. Вероятность события, вычисленная при условии, что имело место другое событие, называетсяусловной вероятностью события и обозначается. Условие независимости событияот событияможно записать в виде:

а условие зависимости - в виде:

Следствие 1. Если событие не зависит от события, то и событиене зависит от события.

Следствие 2. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

Теорема умножения вероятностей может быть обобщена на случай произвольного числа событий. В общем виде она формулируется так.

Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:

В случае независимых событий теорема упрощается и принимает вид:

то есть вероятность произведения независимых событий равна произведению вероятностей этих событий: