51. Коэффициент достоверности аппроксимации. Оценка надёжности по критерию Фишера.

Коэффициент достоверности аппроксимации это значение которое характеризует точность аппроксимации, т. е. показывает на сколько точно теоретическое распределение описывает реальное распределение.

Коэффициент достоверности аппроксимации R² показывает степень соответствия трендовой модели исходным данным. Его значение может лежать в диапазоне от 0 до 1. Чем ближе R² к 1, тем точнее модель описывает имеющиеся данные.

Критерий Фишера используется для оценки значимости модели в целом.

Для оценки используется уравнение следующего вида:

где – коэффициент детерминации, n – количество наблюдений, k – число объясняющих переменных.

Вычисленное по этой формуле значение сравнивается с критическим значением критерия Фишера из таблиц распределения Фишера:

где – уровень значимости,и– степени свободы.

Если в результате сравнения оказывается, что , то при заданном уровне значимостипринимается гипотеза о надежности модели в целом. Если в результате сравнения оказывается, что, то при заданном уровне значимостигипотеза о надежности модели в целом отвергается.

52. Понятие экстраполяции (прогнозирование результатов измерений)

Экстраполяция— это метод прогнозирования, который предполагает, что закономерность развития, действовавшая в прошлом, сохранится и в прогнозируемом будущем.

53. Фундаментальная теорема переноса ошибок имеет вид:

где - корреляционная матрица, – матрица производных функций . Эта формула применяется при оценке функций.

 – это дисперсия D_Y.

Если оценивается несколько функций, то матрица f будет являться матрицей Якоби (используем формулу ).

Получим ковариационную матрицу, диагональные элементы которой соответствуют дисперсии, корень из дисперсии будет соответствовать СКО функций.

Если мы имеем функцию суммы или разности двух независимых величин

 , то квадрат средней квадратической ошибки функции выразится формулой

m_z²=m_x²+m_y² При 

Если функция имеет вид

 ,

 то (14)

 т. е. квадрат средней квадратической ошибки алгебраической суммы аргументов равен сумме квадратов средних квадратических ошибок слагаемых.

Если m₁=m₂=m₃=…=m_n=m,то формула(14) примет вид

 т. е. средняя квадратическая ошибка алгебраической суммы (разности) измеренных с одинаковой точностью величин в  раз больше средней квадратической ошибки одного сла­гаемого.

Если функция имеет вид

То где k₁, k₂, k_з, ..., k_п — постоянные числа; m₁,m₂,m₃,..., т_п — средние квадратические ошибки соответствующих аргументов. Если имеем функцию многих независимых переменных общего вида

то . (15)

Из формулы (15) следует, что квадрат средней квадратиче­ской ошибки функции общего вида равен сумме квадратов про­изведений частных производных по каждому аргументу на среднюю квадратическую ошибку соответствующего аргумента

54. Оценка точности функций зависимых результатов измерений.

Формулы для вычислений средних квадратических ошибок функции u=f(x₁,x₂,….x_n)

имеют вид:

а) в случае некоррелированных аргументов :

m_u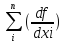²=₀² m_xi²

б) для коррелированных аргументов

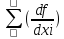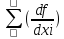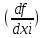m_u²=₀² m_xi²+2_{0 0} r_{xi xj} m_xi m_xj

Для системы функций (вектор-функции) u = f(X)

M_u²= AM²_xA^T где M_u² и M²_x - соответственно эмпирическне корреляционные матрицы вектор-функции и вектора измерений. А - Матрица