46. Методы выявления систематического влияния. Критерии серий.

Значимость систематического влияния определяется на основе выполнения неравенства (1),где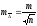-погрешность из среднего арифметического из истинных погрешностей ∆.При отсутствии систематического влияния ,величина среднего ∆ должна равняться нулю. Систематическое влияние считается значимым при невыполнении неравенства −𝑡 ∙ 𝑚𝛥̅ ≤ 𝛥̅ ≤ 𝑡 ∙ 𝑚𝛥̅. При выполнении равенства (1) получают новый ряд ,в среднем свободный от систематического влияния как , а оценку точности выполняют по формуле Бесселя.

Наиболее часто используемые критерии выявления систематических влияний в результатах измерений при условии, что закон распределения неизвестен и количество измерений невелико, это критерий серий и критерий «восходящих» и «нисходящих» серий. Критерии серий относят к критериям, выявляющим значимость систематического влияния только монотонного характера, (сдвиг или тренд) на основе проверки вероятностной независимости среди элементов исследуемого ряда. Для этого производят вычисления следующим образом

1. Строят вариационный ряд и находят медиану med(h)

2. Формируют знаковый ряд из плюсов и минусов по правилу: если значение исходного (невариационного) ряда больше медианы, то вместо i-го числа записывают знак «+», если меньше, то знак «–». Элементы ряда равные med(h) пропускают.

3. Находят количество серий (последовательностей подряд идущих знаков) 𝑣(𝑁)

4. Находят число элементов в наибольшей серии 𝜏(𝑁) Для стохастической независимости и следовательно отсутствия значимого систематического влияния монотонного характера должны одновременно выполняться два неравенства 𝑣(𝑁) > 0.5 ∙ (𝑁 + 1 − 1.96√𝑁 − 1) ,

𝜏(𝑁) > 3.3 ∙ log10(𝑁 + 1). Если хотя бы одно из неравенств не выполняется, то гипотеза об отсутствии систематического влияния в исходных измерениях отвергается с вероятностью ошибки, заключённой в пределах от 0.05 до 0.0975, т.е. с доверительной вероятностью 0.9025 – 0.95. Для его выполнения находят из ряда измерений выборочную медиану med(х). Затем строят знаковый ряд из плюсов и минусов для i-того значения исходного В отличие от критерия серий рассматриваемый далее критерий «восходящих» и «нисходящих» серий выявляет смещение среднего значения не только монотонного характера (тренд или сдвиг), но и более общего, например, периодического характера. В нём также исследуется последовательность знаков, но закон её построения следующий: на месте значения ℎ𝑖 исходного ряда ставится «+», если ℎ𝑖+1 − ℎ𝑖 > 0 и соответственно знак «–» при выполнении неравенства ℎ𝑖+1 − ℎ𝑖 < 0.

47. Методы выявления эффектов автокорреляции. Критерий Дарбина-Уотсона.

1. Графический

2. Метод рядов

3. Критерий Дарбина-Уотсона

Один из более распространенных методов определения автокорреляции в остатках – это расчет критерия Дарбина-Уотсона:

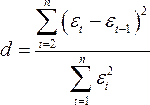Т.е. величина есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.

Можно показать, что при больших значениях существует следующее соотношение между критерием Дарбина-Уотсона и коэффициентом автокорреляции остатков первого порядка :

 . (4.6) Таким образом, если в остатках существует полная положительная автокорреляция и , то . Если в остатках полная отрицательная автокорреляция, то и, следовательно, . Если автокорреляция остатков отсутствует, то и . Т.е. .

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза об отсутствии автокорреляции остатков. Альтернативные гипотезы и состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам (см. приложение E) определяются критические значения критерия Дарбина-Уотсона и для заданного числа наблюдений , числа независимых переменных модели и уровня значимости . По этим значениям числовой промежуток разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью осуществляется следующим образом:

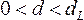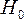•  – есть положительная автокорреляция остатков, отклоняется, с вероятностью 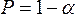принимается ;

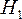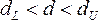•  – зона неопределенности;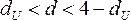

•  – нет оснований отклонять , т.е. автокорреляция остатков отсутствует;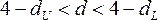

•  – зона неопределенности;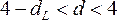

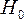•  – есть отрицательная автокорреляция остатков, отклоняется, с вероятностью 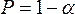принимается .

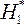Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу .