Лекция 4

10. Статистическая проверка гипотез. Критерий Пирсона

Для проверки гипотезы о соответствии экс- периментального закона распределения случайной величины теоретическому наиболее часто применяют критерий Пирсона или, как его иначе называют, критерий χ² («хи-квадрат»), так как принятие и отклонение гипотезы основаны на χ - распределении.

Предположим, что имеется статистический ряд наблюдений над случайной величинойX. Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина имеет предполагаемый закон распределения, заданный интегральной функцией распределенияF(x) или плотностью вероятностейf(x), который в дальнейшем будем называтьтеоретическим законом распределения.

Первоначально статистический ряд разбивают на k интервалов и подсчитывают число значений случайной величиныX в каждом интервале. В результате получают экспериментальный ряд частот:

m ^' , m ^' , m ^' , , m ^'

1 2 3 k

Следует сразу оговорить, что предпосылкой применения критерия χ² является достаточная заполненность интервалов частотами. На практике рекомендуется иметь в каждом интервале не менее 5-10 наблюдений. Есличисло наблюдений в отдельных интервалах мало, имеет смысл объединить эти интервалы.

38

Исходя из предполагаемого теоретического закона распределения вычисляют частотыт_i в тех самых интервалах, на которые разбит статистический ряд. В результате получают теоретический ряд частот вk интервалахm₁ ,m₂, т₃ ,..., m_к.

Для проверки согласованности теоретического и экспериментального распределения подсчитывают меру расхождения:

(m^' m )²

(m^'

m )²

(m^'

m )²

_ ² _ 1 1 _ 2 2 _{... } k k _,

m₁ m₂ m_k

или

^k (m^' m )²

_ ² _ i i

(10.1)

i1 ^m_i

и число степеней свободы ν. Число степеней свободы равно в этом случае числу интерваловk минус число ограничений f:

ν = k – f (10.2)

Число ограничений равно числу параметров в рассматриваемом законе распределения, увеличенному на единицу. Например, для гауссовского закона имеется два параметра:[М(х) и σ ] в этом случае число ограничений равно трем.

Для распределения χ² составлены специальные таблицы

(см. табл. П2 Приложения ). Пользуясь этими таблицами, можно для каждого значения χ² и числа степеней свободы v определить вероятностьР того, что за счет чисто случайных причин мера расхождения теоретического и

экспериментального распределений (10.1) будет меньше, чем фактически наблюдаемое в данной серии опытов значение χ ².

39

Если эта вероятность Р мала (настолько, что событие с такой вероятностью можно считать практически невозможным), торезультат опыта следует считать противоречащим гипотезе о том, что закон распределения величиныX естьF(х). Эту гипотезу следует отбросить как неправдоподобную.

Напротив, если вероятность Р сравнительно велика, можно признать расхождение между теоретическим и экспериментальным распределениями несущественным и отнестиего за счет случайных причин. Гипотезу о том, что величинаX распределена по законуF(x), можно считать в этом случае правдоподобной, по крайней мере не противоречащей полученным, экспериментальным данным.

В табл. П2 входами являются значение χ² и число

степеней свободы v. Числа, стоящие в таблице, представляют соответствующие значения вероятности Р.

Насколько должна быть мала вероятность Р для того, чтобы отбросить или пересмотреть гипотезу,— вопрос неопределенный.Он не может быть решен из математических соображений, а должен базироваться на априорных сведениях о физической сущности изучаемого процесса.

На практике, если Р<0,1, рекомендуется проверить эксперимент, если возможно — повторить его. В случае появления повторных расхождений следует попытаться найти наиболее подходящий для описания экспериментальных данных закон распределения.

Пример. Пусть в цехе выпускаются такие электронные изделия, как источники питания с постоянным выходным напряжением 200 в. Была сделана выборка из генеральной совокупности и измерены значения параметра качества отобранных изделий. Эти значения образуют непрерывный ряд значений от 190,5 в до 209,5 в. Раз объём этот непрерывный ряд значений на 19 интервалов (см. табл. 10.1). В графе 1 этой таблицы указаны номера интервалов, в графе 2 - границы интервалов, в графе 3- значения середин интервалов, в графе 4 указана частота попадания измеренного значения параметра в

соответствующий интервал. Таким образом, значения, представленные в графах 3 и 4 таблицы 10.1, дают экспериментальное статистическое распределение случайной величины в численной форме. В графической форме этораспределение показано на рис. 6.2 (пунктирная кривая).

Рассмотрим гипотезу осоответствииэкспериментального закона распределения, представленного статистическим рядом в численной форме, а в графической форме на рис. 6.2 (пунктирная кривая), теоретическому (гауссовскому) закону распределения. Для этого используем критерий Пирсона.

В качестве теоретического (гауссовского) закона распределения используем распределение, представленное в численной форме в графах 3 и 5 табл. 10.1 а в графической форме на рис. 8.2 (сплошная кривая). Теоретический ряд, также как и экспериментальный статистический ряд разбиваем на 19 интервалов (табл. 10.1 и рис. 10.1).

Как указывалось выше, предпосылкой применения критерия Пирсона является достаточная заполненность интервалов частотами, т.е. на практике рекомендуется иметь в каждом интервале не менее 5-10 наблюдений. Если число наблюдений в отдельных интервалах мало, то имеет смысл объединить эти интервалы. Если необходимо объединять какое-то количество интервалов экспериментального ряда, тоаналогичные интервалы теоретического ряда тоже объединяются и наоборот.

В нашем случае, чтобы экспериментальные частоты получились не менее 5, необходимо сделать объединение первых четырех интервалов с номерами 1, 2, 3 и 4: (1+2+5+13)=21/4=5,25, что более 5; аналогично, делаем объединение первых четырех интервалов теоретического ряда: (2+4+8+18)=32/4=8.что тоже более5, это означает, что объединение первых четырех интервалов достаточно.

Таблица 10.1 Интервальный ряд случайных величин для экспериментального

(графы 3 и 4) и теоретического

(графы 3 и 5) законов распределения (до объединения интервалов)

Номе р инте рвал а	Границы интервалов (классов)	Середи на интерва ла	Частота m' i эксперимента льного ряда	Частота mi теорети ческого ряда
1	190,5-191,5	191	1	2
2	191,5-192,5	192	2	4
3	192,5-193,5	193	5	8
4	193,5-194,5	194	13	18
5	194,5-195,5	195	30	35
6	195,5-196,5	196	60	60
7	196,5-197,5	197	90	85
8	197,5-198,5	198	97	95
9	198,5-199,5	199	98	99
10	199,5-200,5	200	100	100
11	200,5-201,5	201	98	99
12	201,5-202,5	202	97	95
13	202,5-203,5	203	90	85
14	203,5-204,5	204	60	60
15	204,5-205,5	205	25	35
16	205,5-206,5	206	10	18
17	206,5-207,5	207	3	8
18	207,5-208,5	208	2	4
19	208,5-209,5	209	1	2

Проверим необходимость объединения последних интервалов экспериментального и теоретического рядов. Для экспериментального ряда попробуем объединить четыре последних интервала с номерами 16, 17, 18 и19, вычислим: (10+3+2+1)=16/4=4, т.е. величина менее 5, значит надо объединять последние пять интервалов с номерами 15, 16, 17,

18 и 19 . Вычисления дают: для экспериментального ряда: (25+10+3+2+1)=41/5=8,2, т.е. величина более 5, а для теоретического ряда: (35+18+8+4+2)/5=67/5=13,4, т.е. величина также более 5. Значит, объединение последних пяти интервалов достаточно.

Таблица 10.2 Интервальный ряд случайных величин для экспериментального

(графы 3 и 4) и теоретического (графы 3 и 5) законов распределения (после объединения интервалов).

			Час
			тот
	Границы интервал ов после объедине ния интервал ов	Сер еди на инт ерв ала	а экс пер име нта льн ого ряд	Част ота теорети ческого ряда mi	m’i - mi	(m’i – mi)2	m,  m 2 i i mi
			а,
			m'i
1	2	3	4	5	6	7	8
1	190,5- 194,5	192, 5	5,25	8	2, 75	7,6	0,95
2	194,5- 195,5	195	30	35	5	25	0,71
3	195,5- 196,5	196	60	60	0	0	0

Продолжение табл. 10.2

4	196,5- 197,5	197	90	85	5	25	0,3
5	197,5- 198,5	198	97	95	2	4	0,04
6	198,5- 199,5	199	98	99	1	1	0,01
7	199,5- 200,5	200	100	100	0	0	0,00
8	200,5- 201,5	201	98	99	1	1	0,01
9	201,5- 202,5	202	97	95	2	4	0,04
10	202,5- 203,5	203	90	85	5	25	0,3
11	203,5- 204,5	204	60	60	0	0	0
12	204,5- 209,5	207	8,2	13,4	5, 2	27	2,02
Сумма								4,4

m_i

120

m

100

^m10_m11

m'₁₂

_{m' m}m'^m'10m'₁

m

m

80

m'₁

^{60 m'} m

m'₁ ^m1

40

²⁰ m

m _m m

m

m'₁

m

m₁

⁰ _m' m'

^{m'1 m'}₁ m'₁

x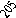

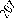
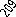
Рис. 10.1. Графики распределения случайных величин для экспериментального (пунктирная линия)

и теоретического (сплошная линия) законов распределения (до объединения интервалов)

Таким образом, после объединения число интервалов станет равным 19-3-4=12. Значения экспериментальных и теоретических частот после объединения интервалов приведены в табл. 10.2 : в графах 3 и 4 для экспериментального распределения, а в графах 3 и 5- для теоретического распределения случайных величин. В табл. 10.2 приведены также значения разностей экспериментальных и теоретических частот для каждого интервала (графа 6), значения их квадратов (графа 7) и значения отношений квадрата разности к соответствующей частоте теоретического ряда (графа 8).

Подставив значения получим

m₁^ и т_i в выражение (2.23),

^k (m^' m )²

^ 2 ^i i= 0,95+0,71+0,0+0,3+0,04+ +0,01+

i1 ^m_i

0,0+0,01+0,04+0,3+0,0+2,02= 4,37

Число степеней свободы в соответствии с (2.24) равно ν =k – f =12 - 3 = 9

По табл. П1 для χ ² = 4,37 и ν = 9 находим, что Р = 0,9.

Следовательно, экспериментальное распределение значений напряжения, приведенное в табл. 10.2 и показанное на рис. 10.1 близко к гауссовскому, что означает отлаженность и стабильность технологического процесса производства.