2.5 Конвективный теплообмен через зернистый слой

При расчете коэффициента теплообмена через зернистый слой применяется уравнение В.Н. Тимофеева при 20Re_ж200

Nu_ж=0,124Re_жPr^0,43(2.28)

при Re_ж200Nu_ж=0,711Re_ж^0,67Pr^0,43(2.29)

Или же уравнения при 20Re_ж200

Nu_ж=0,106Re_ж(2.30)

при Re_ж 200Nu_ж=0,61Re_ж (2.31)

Пример 2.10Слой яблок охлаждается потоком воздуха. Средний размер яблокd=45 мм. Температура воздуха, входящего в слой=0С, выходящего из него -=20С. Скорость фильтрацииw=0,6 м/с.

Определить коэффициент теплообмена от поверхности яблок к воздуху.

Решение.По приложению А таблица А1 определяем теплофизические параметры воздуха при средней температуре2=(0+20)/2=10С.

_ж=2,5110^-2Вт/(мК);_ж=14,1610^-6м²/с,Pr_ж=0,705.

Критерий Рейнольдса .

по (2.31) Nu_ж=0,61Re^0,67=0,61(1779)^0,67=91,82

Вт/(м²К).

Пример 2.11Слой гравия охлаждается водой. Средний размер частицd=27 мм. Температура воды входящей в слой гравия 5С, а выходящий из него=20С. Поверхностная плотность теплового потокаq=2000 Вт/м². Средняя температура поверхности частиц 25С. Определить скорость фильтрации.

Решение.По средней температуре воды2=(5+20)/2=12,5С по приложению А таблица А5 определяем теплофизические свойства воды_ж=57,9510^-2Вт/(мК);_ж=1,24610^-6м²/с,Pr_ж=9,05 приt_ст=25СPr_c=6,22.

q=(t_c-t_ж);Вт/(м²К).

Число Нуссельта .

Предполагая, что Re_ж 200 по (2.29) находим число НуссельтаNu_ж=0,711Re_ж^0,67Pr^0,43. Число Рейнольдса

.

Re=40,66^1/0,67=252,19; м/с.

Задача. Слой зерна после сушилки охлаждается воздухом, средней размер зерна d=8 мм. Температура воздуха входящего в слой зерна 5С, выходящего из него 20С. Скорость фильтрации 0,5 м/с. Определить коэффициент теплоотдачи от зерна к воздуху.

2.6 Теплоотдача суспензий

Во многих отраслях промышленности и сельского хозяйства приходится нагревать или охлаждать жидкостные суспензии мелкодисперсного порошка твердого тела в жидкости.

Согласно экспериментам проводимым в МВТУ им. Н.Э. Баумана Кафановым В.И. критериальное уравнение теплообмена при течении жидкостных суспензий в трубах имеет вид

, (2,32)

где Nu_с – критерий Нуссельта суспензии;

Re_c– критерий Рейнольдса суспензии;

Pr_c– критерий Прандтля суспензии;

r– объемная доля порошка твердого тела в суспензии

_ж– плотность жидкости, кг/м³;

_т- плотность твердого тела, кг/м³;

и - теплоемкости жидкости и твердого тела, кДж/(кгК);

d_триd_r– диаметр трубы и средней диаметр частиц порошка твердого тела.

В качестве определяющей температуры принимают среднюю температуру среды t_ср=(t₁+t₂)/2, гдеt₁– температура среды на входе в теплообменник, аt₂– на выходе из него,С.

Коэффициент гидравлического сопротивления определяют по формуле:

. (2.33)

Теплопроводность суспензии _сопределяют по формуле Максвелла

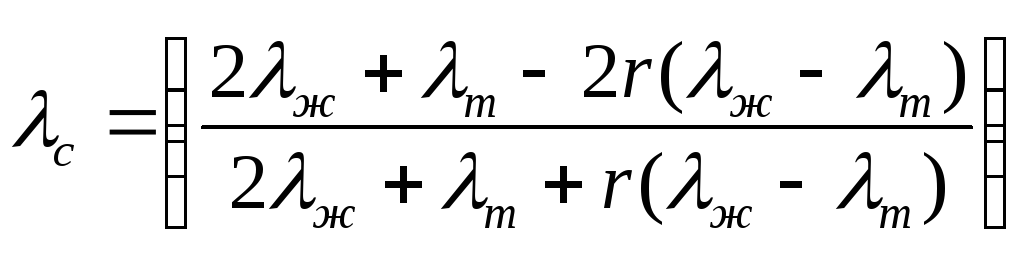, (2.34)

где _ж– теплопроводность жидкости, Вт/(мК);

_т– теплопроводность твердого тела, Вт/(мК).

Динамическая вязкость суспензии _сопределяют по формуле Вэнда

_с=_ж(1+2,5r+7,17r²+16,2r³), (2.35)

где _ж– динамическая вязкость жидкости, Пас.

Выше перечисленными зависимостями можно пользоваться до 25% концентрации по объему.

Пример 2.12 По трубопроводу диаметром 50 мм и длиной 4 м протекает суспензия порошка меди в воде со скоростьюw=1 м/с. Объемная концентрация меди 10%, средний диаметр частиц порошка 10010^-6м. Определить количество теплоты передаваемой суспензии за 1 час, если температура жидкости 50С, а температура стенки 70С, а также коэффициент теплообмена.

Решение.Подсчитываем отдельные множители, входящие в управление (2.32). Теплофизические параметры берем из приложения А таблица А5 и таблица Б1 приложения Б.

_с=_тr+_ж(i+r)=89300,1+988,1(1+0,1)=1769,29 кг/м³

По формуле (2.35) определяем динамическую вязкость суспензии

_с=_ж(1+2,5r+7,17r²+16,2r³)=543,410^-6(1+2,50,1+7,17(0,1)²+16,2(0,1)³=73510^-6Нс/м²=73510^-6Пас.

По формуле (2.34) находим _ссуспензии

По формуле

вычисляем теплоемкость суспензии.

Находим число Рейнольдса .

Число Прандтля

Число Нуссельта

Находим коэффициент теплообмена _с

Вт/(м²К)

По закону Ньютона-Рихмана

Ф=_сА(t_с-t_ж)=58243,140,05420=73149 Вт